PyTorch基础(六)-- optim模块
PyTorch的optim是用于参数优化的库(可以说是花式梯度下降),optim文件夹主要包括1个核心的父类(optimizer)、1个辅助类(lr_scheduler)以及10个常用优化算法的实现类。optim中内置的常用算法包括adadelta、adam、adagrad、adamax、asgd、lbfgs、rprop、rmsprop、sgd、sparse_adam。
1 核心类optimizer
Optimizer类是所有优化方法的父类,它保存参数状态并根据梯度将其更新。这里将分享Optimizer类的构造方法和有关梯度控制的两个方法。构造方法指的是_init_()方法,梯度控制方法包括大家经常用到的的zero_grad()和step()。
1.1 构造方法init()
Optimizer的init函数接收两个参数:第一个是需要被优化的参数,其形式必须是Tensor或者dict;第二个是优化选项,包括学习率、衰减率等。第一个位置通常用model.parameters()填充,如果有特殊的需求,也可以手动写一个dict来作为输入。这时只需要保证dict中有一个['params']键即可,其他键可以按照自己的要求填写。
# 构建一个optimizer对象
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
当我们想指定每一层的学习率时,我们可以这样做,每一个dict都分别定义一组参数,并且包含一个param键,这个键对应参数的列表。其他的键应该optimizer所接受的其他参数的关键字相匹配,并且会被用于对这组参数的优化。
# model.base的参数将会使用1e-2的学习率,model.classifier的参数将会使用1e-3的学习率,并且0.9的momentum将会被用于所有的参数。
optim.SGD([{'params': model.base.parameters()},
{'params': model.classifier.parameters(), 'lr': 1e-3}],
lr=1e-2, momentum=0.9)
1.2 梯度控制方法zero_grad()和step()
在进行反向传播之前,必须要用zero_grad()清空梯度。所有的optimizer都实现了step()方法,这个方法会更新所有的参数。它能按两种方式来使用:
方式一: 大多数optimizer所支持的简化版本:optimzer.step()
for input, target in dataset:
optimizer.zero_grad() # zero grad
output = model(input) # forward: predict
loss = loss_fn(output, target) # forward: loss
loss.backward() # backward: autograd
optimizer.step() # update param
方式二: 一些优化算法例如Conjugate Gradient和LBFGS需要重复多次计算函数,因此你需要传入一个闭包去允许它们重新计算你的模型。这个闭包应当清空梯度, 计算损失,然后返回。如下:
for input, target in dataset:
def closure():
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
return loss
optimizer.step(closure)
2 辅助类lr_scheduler
在深度学习训练过程中,最重要的参数就是学习率,通常来说,在整个训练过层中,学习率不会一直保持不变,为了让模型能够在训练初期快速收敛,学习率通常比较大,在训练末期,为了让模型收敛在更小的局部最优点,学习率通常要比较小。
lr_scheduler用于在训练过程中根据轮次灵活调控学习率。调整学习率的方法有很多种,但是其使用方法是大致相同的:用一个Schedule把原始Optimizer装饰上,然后再输入一些相关参数,然后用这个Schedule做step()。Pytorch提供了六种学习率调整方法,可分为三大类,分别是:
- 有序调整
Step/MultiStep/ Exponential/CosineAnnealin - 自适应调整
ReduceLROnPlateau - 自定义调整
Lambda
了解更多请参考:lr_scheduler用法总结
3 优化算法
神经网络的学习的目标是找到损失函数的值尽可能小的参数,这是寻找最优参数的问题,解决该问题的过程称为最优化。
3.1 随机梯度下降算法 SGD 算法
用单个训练样本的损失来近似平均损失,即每次随机采样一个样本来估计当前梯度,对模型参数进行一次更新。
θ t + 1 = θ t − η ∇ L ( θ t ; x i , y i ) ⏟ g t θ t + 1 = θ t − η g t \theta_{t+1}=\theta_t-\eta\underbrace{\nabla L(\theta_t;x_i,y_i)}_{g_t}\\ \theta_{t+1}=\theta_t-\eta g_t θt+1=θt−ηgt ∇L(θt;xi,yi)θt+1=θt−ηgt
class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float) | 学习率 |
| momentum (float, 可选) | 动量因子(默认:0,通常设置为0.9,0.8) |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认:0) |
| dampening (float, 可选) | 动量的抑制因子(默认:0) |
| nesterov (bool, 可选) | 使用Nesterov动量(默认:False) |
优点:(1)使用
mini-batch的时候,可以收敛得很快;(2)训练速度快,内存开销小。
缺点:(1)在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确;(2)SGD每步接受的信息有限,对梯度的估计准确性低,造成目标函数的收敛不稳定伴有震荡甚至出现不收敛。随机性大,并不保证全局最优化。
推荐程度: 不推荐
1. SGD+Momentum
更新的时候在一定程度上保留之前更新的方向,可以加速SGD,抑制震荡,用法为在torch.optim.SGD的momentum参数不为零。具体公式为:
m t = β 1 m t − 1 + η ∇ L ( θ t ) θ t + 1 = θ t − m t m_{t}=\beta_1 m_{t-1}+\eta\nabla L(\theta_t)\\ \theta_{t+1}=\theta_t-m_t mt=β1mt−1+η∇L(θt)θt+1=θt−mt
优点: 比
SGD收敛更快,目标函数的收敛更稳定,减少在鞍点等的震荡。
缺点: 保持惯性,缺乏适应性。梯度方向不变的维度上更新速度变快,梯度方向有所改变的维度上的更新速度变慢。
推荐程度: 可以一试
2. SGD+NAG
使用牛顿加速度(NAG, Nesterov accelerated gradient)的随机梯度下降法(SGD),在SGD+Momentum上增加“提前量”设计,在计算梯度时做了调整,用 θ t − β 1 m t − 1 \theta_t-\beta_1 m_{t-1} θt−β1mt−1来近似当作参数下一步会变成的值,计算未来可能位置处的梯度而非当前位置的梯度。
m t = β 1 m t − 1 + η ∇ L ( θ t − β 1 m t − 1 ) θ t + 1 = θ t − m t m_{t}=\beta_1 m_{t-1}+\eta\nabla L(\theta_t-\beta_1 m_{t-1})\\ \theta_{t+1}=\theta_t-m_t mt=β1mt−1+η∇L(θt−β1mt−1)θt+1=θt−mt
优点: 改进
Momentum方法,防止按照惯性走的太快,会衡量一下梯度做出修正。
缺点: 对收敛率的作用却不是很大
推荐程度: 不如不试
关于批量梯度下降法(batch gradient descent, BGD),随机梯度下降法( stochastic gradient descent, SGD), 以及小批量梯度下降法(mini-batch gradient descent, MBGD)的具体内容可以参考:
- 几种梯度下降方法对比:https://blog.csdn.net/u012328159/article/details/80252012
- 批梯度下降法(Batch Gradient Descent ),小批梯度下降 (Mini-Batch GD),随机梯度下降 (Stochastic GD):https://blog.csdn.net/cs24k1993/article/details/79120579
- 批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解:https://www.cnblogs.com/lliuye/p/9451903.html
3.2 平均随机梯度下降算法 ASGD算法
随机平均梯度下降(Averaged Stochastic Gradient Descent,AGSD)就是用空间换时间的一种SGD。详细可参看论文:http://riejohnson.com/rie/stograd_nips.pdf
class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认:1e-2) |
| lambd (float, 可选) | 衰减项(默认:1e-4) |
| alpha (float, 可选) | eta更新的指数(默认:0.75) |
| t0 (float, 可选) | 指明在哪一次开始平均化(默认:1e6) |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认: 0) |
推荐程度: 很少见
3.3 自适应优化 AdaGrad算法
Adagrad是一种自适应优化方法,是自适应的为各个参数分配不同的学习率。这个学习率的变化,会受到梯度的大小和迭代次数的影响。梯度越大,学习率越小;梯度越小,学习率越大。对更新频率低的参数做较大的更新,对更新频率高的参数做较小的更新。采用“历史梯度平方和”来衡量不同参数的梯度的稀疏性,取值越小表明越稀疏。
θ t + 1 , i = θ t , i − η ∑ k = 0 t g k , i 2 + ϵ g t , i \theta_{t+1,i}=\theta_{t,i}-\frac{\eta}{\sqrt{\sum_{k=0}^{t}g_{k,i}^2}+\epsilon}g_{t,i} θt+1,i=θt,i−∑k=0tgk,i2+ϵηgt,i
详细公式请阅读:Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
John Duchi, Elad Hazan, Yoram Singer; 12(Jul):2121−2159, 2011.(http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf)
class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认: 1e-2) |
| lr_decay (float, 可选) | 学习率衰减(默认: 0) |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认: 0) |
优点: 它可以自动调节学习率,减少学习率的手动调整,更适用于稀疏或者分布不平衡的数据,提高SGD的鲁棒性。
缺点: 仍依赖于人工设置一个全局学习率,随着迭代次数增多,分母会不断累积,学习率衰减越来越快,最终会趋近于0。
推荐程度: 不推荐
3.4 自适应学习率调整 AdaDelta算法
针对AdaGrad改进:因为AdaGrad采用所有历史梯度平方和的平方根做分母,分母随时间单调递增,产生的自适应学习速率随时间衰减的速度过于激进 。AdaDelta采用指数衰减平均的计算方法,用过去梯度平方的衰减平均值代替他们的求和。 这个分母相当于梯度的均方根root mean squared (RMS),在数据统计分析中,将所有值平方求和,求其均值,再开平方,就得到均方根值。
θ t + 1 = θ t − R M S [ Δ θ ] t − 1 R M S [ g ] t g t E [ g 2 ] t = γ E [ g 2 ] t − 1 + ( 1 − γ ) g t 2 E [ Δ θ 2 ] t = γ E [ Δ θ 2 ] t − 1 + ( 1 − γ ) Δ θ t 2 \theta_{t+1}=\theta_t-\frac{RMS[\Delta\theta]_{t-1}}{RMS[g]_t}g_t\quad \\ E[g^2]_t=\gamma E[g^2]_{t-1}+(1-\gamma)g_t^2\\ E[\Delta \theta^2]_t=\gamma E[\Delta \theta^2]_{t-1}+(1-\gamma)\Delta \theta_t^2 θt+1=θt−RMS[g]tRMS[Δθ]t−1gtE[g2]t=γE[g2]t−1+(1−γ)gt2E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθt2
详细公式请阅读:https://arxiv.org/pdf/1212.5701.pdf
class torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| rho (float, 可选) | 用于计算平方梯度的运行平均值的系数(默认:0.9) |
| eps (float, 可选) | 为了增加数值计算的稳定性而加到分母里的项(默认:1e-6) |
| lr (float, 可选) | 在delta被应用到参数更新之前对它缩放的系数(默认:1.0) |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认: 0) |
优点: 不需要提取设定学习速率,使用指数衰减平均计算,避免在训练后期,学习率过小;初期和中期,加速效果不错,训练速度快。
缺点: 还是需要自己手动指定初始学习率,初始梯度很大的话,会导致整个训练过程的学习率一直很小,在模型训练的后期,模型会反复地在局部最小值附近抖动,从而导致学习时间变长
推荐程度: 可以试一试更好的
3.5 弹性反向传播 Rprop算法
实现Rprop优化方法(弹性反向传播),优化方法原文《Martin Riedmiller und Heinrich Braun: Rprop - A Fast Adaptive Learning Algorithm. Proceedings of the International Symposium on Computer and Information Science VII, 1992》。该优化方法适用于full-batch,不适用于mini-batch,因而在min-batch大行其道的时代里,很少见到。
具体算法流程为:(1)首先为各权重变化赋一个初始值,设定权重变化加速因子与减速因子;(2)在网络前馈迭代中当连续误差梯度符号不变时,采用加速策略,加快训练速度;当连续误差梯度符号变化时,采用减速策略,以期稳定收敛。(3)网络结合当前误差梯度符号与变化步长实现BP,同时,为了避免网络学习发生振荡或下溢,算法要求设定权重变化的上下限。
class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认:1e-2) |
| etas (Tuple[float,float], 可选) | 一对(etaminus,etaplis), 它们分别是乘法的增加和减小的因子(默认:0.5,1.2) |
| step_sizes (Tuple[float,float], 可选) | 允许的一对最小和最大的步长(默认:1e-6,50) |
缺点: 优化方法适用于
full-batch,不适用于mini-batch,因此基本上没什么用
推荐程度: 不推荐!不能用在mini-batch,想不到在什么时候能用
3.6 均方根传递 RMSprop算法
Root Mean Square Prop,均方根传递是Geoff Hinton提出的一种自适应学习率方法。RMSprop和Adadelta一样,也是对Adagrad的一种改进。RMSprop采用均方根作为分母,可缓解Adagrad学习率下降较快的问题。并且引入均方根,可以减少摆动,同时结合了Momentum的惯性原则,加上AdaGrad对错误方向的阻力。但是缺少了Momentum的一部分,因此后面Adam补上这个想法。详细了解请参考:http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
RMSprop和AdaDelta都是为了解决AdaGrad学习率急剧下降问题的。
v t = β 1 v t − 1 + ( 1 − β 1 ) g t 2 θ t + 1 = θ t − η v t + ϵ g t v_t = \beta_1 v_{t-1}+(1-\beta_1)g_t^2\\ \theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{v_t+\epsilon}}g_t vt=β1vt−1+(1−β1)gt2θt+1=θt−vt+ϵηgt
class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认:1e-2) |
| momentum (float, 可选) | 动量因子(默认:0) |
| alpha (float, 可选) | 平滑常数(默认:0.99) |
| eps (float, 可选) | 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) |
| centered (bool, 可选) | 如果为True,计算中心化的RMSProp,并且用它的方差预测值对梯度进行归一化 |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认: 0) |
优点: 可缓解
Adagrad学习率下降较快的问题,并且引入均方根,可以减少摆动,适合处理非平稳目标,对于RNN效果很好
缺点: 依然依赖于全局学习率
推荐程度: 推荐!RMSProp算法在经验上已经被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一
3.7 自适应矩估计 Adam算法
结合Momentum和AdaGrad的优点,即考虑过去梯度的平方的指数衰减平均值,也保持过去梯度的指数衰减平均值。还包含了偏置修正,利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。详细了解请参考:https://arxiv.org/pdf/1412.6980.pdf。公式如下:
m t = β 1 m t − 1 + ( 1 − β 1 ) g t v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 m t ^ = m t 1 − β 1 t v t ^ = v t 1 − β 2 t θ t + 1 = θ t − η v t ^ + ϵ m t ^ m_t=\beta_1m_{t-1}+(1-\beta_1)g_t\\ v_t=\beta_2v_{t-1}+(1-\beta_2)g_t^2\\ \hat{m_t}=\frac{m_t}{1-\beta_1^t}\quad \hat{v_t}=\frac{v_t}{1-\beta_2^t}\\ \theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{\hat{v_t}+\epsilon}}\hat{m_t} mt=β1mt−1+(1−β1)gtvt=β2vt−1+(1−β2)gt2mt^=1−β1tmtvt^=1−β2tvtθt+1=θt−vt^+ϵηmt^
class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认:1e-3) |
| betas (Tuple[float,float], 可选) | 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999) |
| eps (float, 可选) | 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认: 0) |
优点:(1)为不同参数产生自适应的学习速率;(2)对目标函数没有平稳要求,即
loss function可以随着时间变化 ;(3)参数的更新不受梯度的伸缩变换影响;(4)更新步长和梯度大小无关,只和alpha、beta_1、beta_2有关系。并且由它们决定步长的理论上限;(5)更新的步长能够被限制在大致的范围内(初始学习率) ;(6)能较好的处理噪音样本,能天然地实现步长退火过程(自动调整学习率);(7)很适合应用于大规模的数据及参数的场景、不稳定目标函数、梯度稀疏或梯度存在很大噪声的问题
推荐程度: 非常推荐,基本上是最最常用的优化方法
3.8 Adamax算法(Adamd的无穷范数变种)
Adamax优化器来自于Adam的论文的Section7,该方法是基于无穷范数的Adam方法的变体,对梯度平方的处理由指数衰减平均改为指数衰减求最大值。在Adam中,单个权重的更新规则是将其梯度与当前和过去梯度的 L 2 L_2 L2 范数(标量)成反比例缩放。作者又将基于 L 2 L_2 L2范数的更新规则泛化到基于 L p L_p Lp范数的更新规则中。
v t = β 2 p v t − 1 + ( 1 − β 2 p ) ∣ g t ∣ p = ( 1 − β 2 p ) ∑ i t β 2 p ( t − i ) ⋅ ∣ g i ∣ p \begin{aligned}v_t&=\beta_2^{p}v_{t-1}+(1-\beta_2^{p})|g_t|^p\\&=(1-\beta_2^{p})\sum_{i}^{t}\beta_2^{p(t-i)}\cdot|g_i|^p\end{aligned} vt=β2pvt−1+(1−β2p)∣gt∣p=(1−β2p)i∑tβ2p(t−i)⋅∣gi∣p
虽然这样的变体会因为 p p p的值较大而在数值上变得不稳定,但是在特例中,令 p → ∞ p\rightarrow\infty p→∞会得出一个极其稳定和简单的算法。
u t = lim p → ∞ ( v t ) 1 / p = m a x ( β 2 ⋅ u t − 1 , ∣ g t ∣ ) \begin{aligned}u_t&=\lim_{p\rightarrow\infty}(v_t)^{1/p} \\&= max(\beta_2\cdot u_{t-1},|g_t|)\end{aligned} ut=p→∞lim(vt)1/p=max(β2⋅ut−1,∣gt∣)
由于 u t u_t ut依赖于max操作,所以AdaMax不像在Adam中 m t m_t mt和 v t v_t vt的偏差趋向于0,所以不需要计算 u t u_t ut的偏差校正( u 0 = 0 u_0=0 u0=0)。
m t = β 1 m t − 1 + ( 1 − β 1 ) g t u t = max ( β 2 u t − 1 , ∣ g t ∣ ) θ t + 1 = θ t − η u t m t m_t=\beta_1m_{t-1}+(1-\beta_1)g_t\\ u_t=\max(\beta_2u_{t-1},|g_t|)\\ \theta_{t+1}=\theta_t-\frac{\eta }{u_t}m_t mt=β1mt−1+(1−β1)gtut=max(β2ut−1,∣gt∣)θt+1=θt−utηmt

class torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认:2e-3) |
| betas (Tuple[float,float], 可选) | 用于计算梯度以及梯度平方的运行平均值的系数 |
| eps (float, 可选) | 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认: 0) |
优点: 对学习率的上限提供了一个更简单的范围
推荐程度: 非常推荐!其实也就是Adam的一个变种,差不了多少
3.9 Nadam
Adam的改进版,类似于带有Nesterov动量项的Adam,Nadam对学习率有了更强的约束,同时对梯度的更新也有更直接的影响。公式如下:
g t ^ = g t 1 − Π i = 1 t μ i m t = μ t ∗ m t − 1 + ( 1 − μ t ) ∗ g t m t ^ = m t 1 − Π i = 1 t + 1 μ i n t = ν ∗ n t − 1 + ( 1 − ν ) ∗ g t 2 n t ^ = n t 1 − ν t m t ˉ = ( 1 − μ t ) ∗ g t ^ + μ t + 1 ∗ m t ^ Δ θ t = − η ∗ m t ˉ n t ^ + ϵ \hat{g_t}=\frac{g_t}{1-\Pi_{i=1}^t\mu_i}\\m_t=\mu_t*m_{t-1}+(1-\mu_t)*g_t \\ \hat{m_t}=\frac{m_t}{1-\Pi_{i=1}^{t+1}\mu_i}\\ n_t=\nu*n_{t-1}+(1-\nu)*g_t^2\\ \hat{n_t}=\frac{n_t}{1-\nu^t}\bar{m_t}=(1-\mu_t)*\hat{g_t}+\mu_{t+1}*\hat{m_t}\\\Delta{\theta_t}=-\eta*\frac{\bar{m_t}}{\sqrt{\hat{n_t}}+\epsilon} gt^=1−Πi=1tμigtmt=μt∗mt−1+(1−μt)∗gtmt^=1−Πi=1t+1μimtnt=ν∗nt−1+(1−ν)∗gt2nt^=1−νtntmtˉ=(1−μt)∗gt^+μt+1∗mt^Δθt=−η∗nt^+ϵmtˉ
Nadam对学习率有了更强的约束,同时对梯度的更新也有更直接的影响。一般而言,在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果。
3.10 L-BFGS
经典的优化问题中迭代法的一阶法(梯度下降法),前面SGD、Adam等都是在一阶法的基础上进行改进,加快收敛速率。二阶法(牛顿法)的收敛速度是远快于一阶法的,但是Hessian矩阵求逆的计算复杂度很大,对于目标函数非凸时,二阶法有可能会收敛到鞍点。针对二阶法的这个问题,提出了BFGS算法,再是低存储的L-BFGS算法。简答说L-BFGS和梯度下降、SGD干的同样的事情。
class torch.optim.LBFGS(params, lr=1, max_iter=20, max_eval=None, tolerance_grad=1e-05, tolerance_change=1e-09, history_size=100,line_search_fn=None)
| 参数 | 描述 |
|---|---|
| lr (float) | 学习率(默认:1) |
| max_iter (int) | 每一步优化的最大迭代次数(默认:20) |
| max_eval (int) | 每一步优化的最大函数评价次数(默认:max * 1.25) |
| tolerance_grad (float) | 一阶最优的终止容忍度(默认:1e-5) |
| tolerance_change (float) | 在函数值/参数变化量上的终止容忍度(默认:1e-9) |
| history_size (int) | 更新历史的大小(默认:100) |
优点: 收敛速度快、内存开销少,是解无约束非线性规划问题最常用的方法
缺点: 使用条件严苛
推荐程度: 酌情选择,根据自己的需要考虑是否真的需要使用这个算法
了解更多,请阅读:深入机器学习系列17-BFGS & L-BFGS
3.11 SparseAdam
针对稀疏张量的一种“阉割版”Adam优化方法。
class torch.optim.SparseAdam(params,lr=0.001,betas=(0.9,0.999),eps=1e-0
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认:2e-3) |
| betas (Tuple[float,float], 可选) | 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999) |
| eps (float, 可选) | 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) |
优点: 相当于Adam的稀疏张量专用版本
推荐程度: 推荐,在处理稀疏张量的时候尤其推荐
3.12 AdamW
在Ilya Loshchilov & Frank Hutter 的论文Decoupled weight decay regularization中,把Adam中的权重衰减和基于损失的梯度更新解耦(AdamW)。发现在Adam这种自适应学习率算法中 L 2 L_2 L2正则化不像在SGD中有效:
- L 2 L_2 L2正则化和
Weight Decay并不等价,只有在标准的SGD下可以把两者等价。特别当与自适应梯度相结合时, L 2 L_2 L2正则化导致具有较大历史参数或梯度幅度的权重比使用权重衰减时更小。 - 使用Adam优化带 L 2 L_2 L2正则的损失并不有效。如果引入 L 2 L_2 L2正则化项,在计算梯度的时候会加上正则项求梯度的结果。正常的权重衰减是对所有的权重都采用相同的系数进行更新,本身比较大的一些权重对应的梯度也会比较大,惩罚也越大。但由于Adam计算步骤中减去项会有除以梯度平方的累积,使得梯度大的减去项偏小,从而具有大梯度的权重不会像解耦权重衰减那样得到正则化。 这导致自适应梯度算法的 L 2 L_2 L2和解耦权重衰减正则化的不等价。
而在常见的深度学习库中只提供了 L 2 L_2 L2正则,并没有提供权重衰减的实现。这可能就是导致Adam跑出来的很多效果相对SGD with Momentum有偏差的一个原因。大部分的模型都会有 L 2 L_2 L2 regularization约束项,因此很有可能出现Adam的最终效果没有SGD的好。目前bert训练采用的优化方法就是AdamW,对除了layernorm,bias项之外的模型参数做weight decay。

Adam的weight decay发生在紫字部分,所以由于 g 2 g^2 g2作分母,会使得大的梯度得不到足够力度的正则化;而AdamW把weight decay放在了绿字部分,所以能有效的正则化。
class torch.optim.AdamW(params,lr=0.001,betas=(0.9,0.999),eps=1e-08,weight_decay=0.01,amsgrad=False)
| 参数 | 描述 |
|---|---|
| params (iterable) | 待优化参数的iterable或者是定义了参数组的dict |
| lr (float, 可选) | 学习率(默认:1e-3) |
| betas (Tuple[float,float], 可选) | 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999) |
| eps (float, 可选) | 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8) |
| weight_decay (float, 可选) | 权重衰减(L2惩罚)(默认: 1e-2) |
| amsgrad(boolean, optional) | 是否使用从论文On the Convergence of Adam and Beyond中提到的算法的AMSGrad变体(默认:False) |
优点:比Adam收敛得更快
缺点:只有fastai使用,缺乏广泛的框架,而且也具有很大的争议性
下面是一些算法的对比动图,便于我们对常用的优化方法的收敛速度有一个更直观的认识。


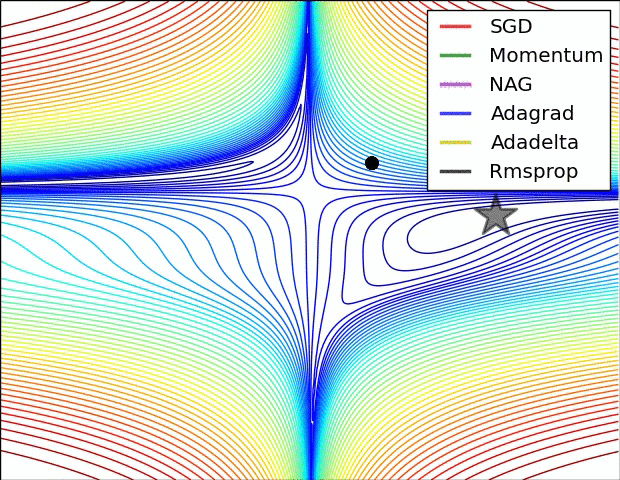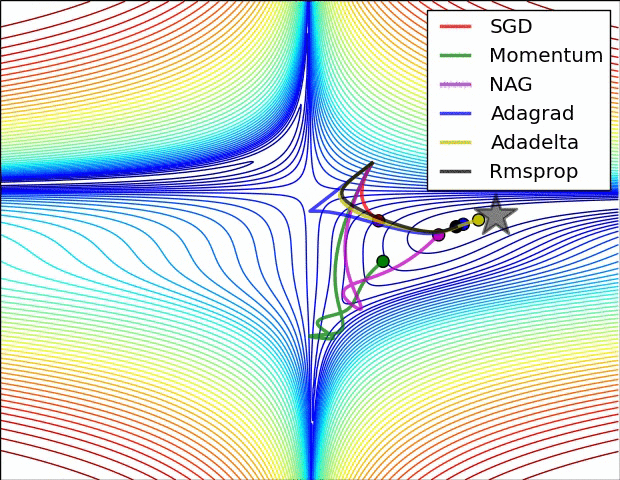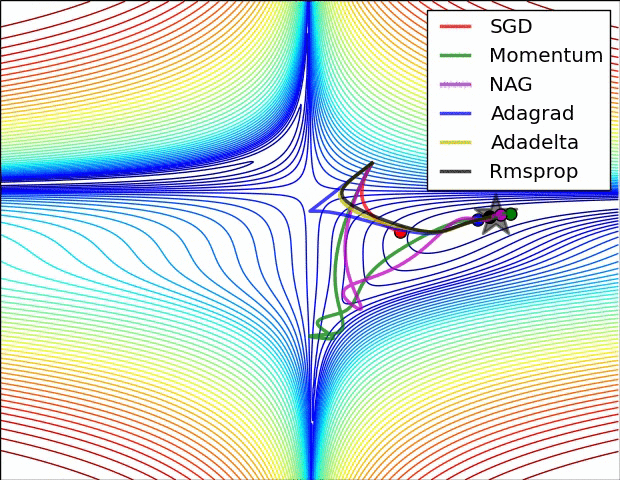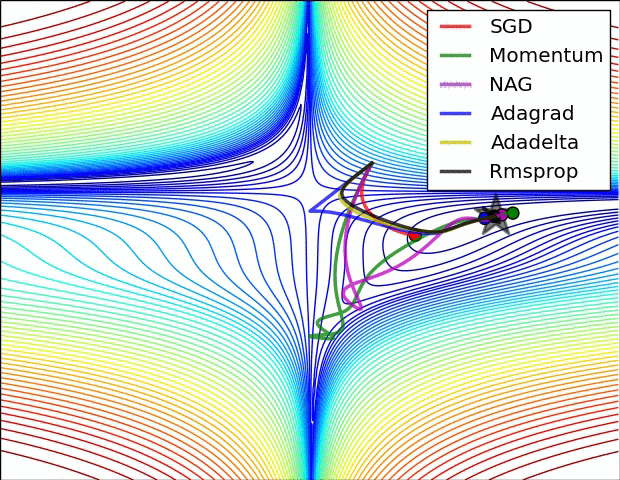
以上内容仅做学习使用,主要借鉴自文末资料,在此感谢各位作者的整理,如果对你有帮助,欢迎点赞收藏。
参考
- torch.optim:https://pytorch-cn.readthedocs.io/zh/latest/package_references/torch-optim/
- 各种优化器SGD,AdaGrad,Adam,LBFGS都做了什么?:https://blog.csdn.net/u012744245/article/details/112671504
- PyTorch的十个优化器:https://blog.csdn.net/tototuzuoquan/article/details/113779970
- 学习PyTorch的optim模块:https://zhuanlan.zhihu.com/p/41127426
- 卷积神经网络中的优化算法比较:https://shuokay.com/2016/06/11/optimization/
- 优化算法:https://blog.csdn.net/qq_36717487/article/details/122253746