论文阅读：Burst photography for high dynamic range and low-light imaging

Introduction

Google HDR+ 技术曾使得Google pixel 2以其单镜头拍照质量超越了众多双摄手机，登顶手机拍照质量排行榜。这篇文章是HDR+初代版本的技术细节的介绍，与其他HDR技术论文相比，其更加注重工程实用化以及整个成像系统，因此也引入了很多工程化的技巧，以求得在手机设备上达到理想效果。
对于手机来说，为了便携化，一般其相机的镜头光圈较小，限制了射入光子的数量，使得在暗光场景下噪声剧烈。同时其传感器像素小，限制了每个像素存储的点在数，导致了动态范围有限。另外，手机用户对算法的速度要求高，为了实现快速响应难免要牺牲一定的图像质量。以及手机的内存和电源都是相对有限的。这些都是这项技术需要考虑的问题。一个好的成像算法应该满足处理迅速、算法自动、结果自然、且在多种环境下成像质量优于传统算法。
为此，这篇文章提出了以下几点改进：

1. 拍摄多帧相同曝光图像，有利于更加鲁棒的配准，同时曝光设定的足够低，从而避免出现过曝光区域；
2. 直接获取Bayer raw图像进行处理，而不是经过ISP后处理的RGB图像，从而获取更多的图像信息；
3. 提出了新的基于FFT的配准方法，以及基于图像对的维纳滤波融合方法，使得融合结果对运动和噪声更加鲁棒；

Overview

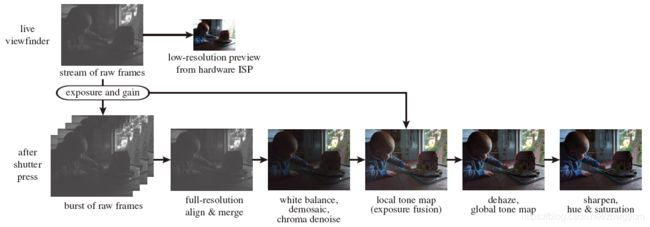
成像系统包括两个流程，一个产生实时显示的低分辨取景器流，一个输出非实时的单张高质量图像。
使用raw图像有几个优点：

1. 动态范围高：raw图像像素一般是10 bit的，高于一般的RGB图像的8 bit；
2. 线性：raw图像与场景亮度成正比（去掉暗电流后），使得对传感器噪声建模更加准确，从而对准和融合也更加鲁棒，自动曝光更加简单；
3. 可移植性：便于移植到新的相机中。

Auto-exposure

为了处理高动态范围场景，文章提出了三个步骤：

1. 刻意欠曝光以防止像素过饱和；
2. 获取多帧图像用于阴影区域的降噪；
3. 使用局部色调映射压缩动态范围；
   自动曝光算法就是用来决定使用什么曝光参数，如何压缩动态范围，以及拍摄多少帧图像。
   通过自动曝光算法，输出两种曝光水平的图像，一张短曝光图像，用于捕捉场景；一张合成的长曝光图像，被用来做HDR色调映射。
   当然，为了使得图像看起来更真实，压缩的动态范围也不能太大，文章限制最大动态范围压缩比例为8。

基于实例的自动曝光

自动选择曝光的一个主要困难在于曝光是场景依赖的。对于不同的场景需要设置不同的曝光参数。因此，文章建立了一个数据集，其使用传统的HDR曝光的方法获取了多个场景。并且使用文章的色调映射的方法手动调节参数使得输出图像看起来尽可能的自然。数据集包含了5000个场景，覆盖了日常见到的大部分场景，并手动标定两个参数分别对应长短曝光。
有了这些标定的数据集，对于输入的一帧raw图像，计算其描述子并在数据集中搜素与其匹配的场景。一旦找到了一系列候选的匹配场景，计算这些场景被手动标定好的自动曝光参数的加权混合值。这个加权混合值最终会产生两个参数：短曝光和长曝光值。

曝光参数

曝光参数包括曝光时间和增益（ISO值）。对于最亮的场景，保持增益在最小水平，使得曝光时间增加到8ms。然后随着场景变暗，保持8ms的曝光时间，增加增益到4倍。最后，同时增加曝光时间和增益直到100ms曝光时间和96倍增益。为了最大化SNR，尽量使用模拟方式增加增益，直到超过相机限制后再使用数字增益。

图像数量

实践中，一般拍摄2到8张图像，使用raw图像噪声模型的信息做决策。
为了节省能量，每四帧运行一次自动曝光算法。

Aligning Frames

为了兼顾速度和配准精度，并考虑到手机内存和电量有限的情况，文章提出了一种简单的基于频域加速的配准方法。其可以实现在移动设备上24ms/Mpix的速度。

参考帧的选择

像lucky imaging一样，根据基于raw图像绿色通道梯度的简单测量方法，选择多帧图像中最清晰的一张最为参考图像。同时，为了减少快门延迟，从前3帧图像中选择参考图像。

处理raw图像

将raw图像中每一个RGGB的Bayer采样做平均，使得原raw图像下采样4倍得到灰度图像，对该灰度图像做配准。

分层配准

在四层高斯金字塔中，使用coarse-to-fine的策略分层配准。如下图所示，在每层金字塔中，使用基于块的对准方法，并使用上层配准好的结果作为初始估计值。

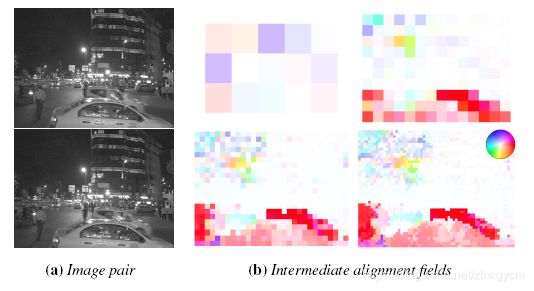
使用下式作为每个块的偏移量测量，通过优化下式实现每个块的配准：
$$D_p(u,v)=\sum _{y=0}^{n-1}\sum _{x=0}^{n-1}|T(x,y)-I(x+u+u_0,y+v+v_0){|}^p\text{\hspace{1em}(1)}$$

其中，$T$是参考图像的一个块，$I$是待对准图像中的搜索区域，$p$是范数的幂，$n$是块的大小，$(u_0,v_0)$是从上一层传递下来的初始的位置估计。
公式中有一系列的参数需要确定，如块的大小，搜索半径，范数的选择等。其中有一条重要的依据是根据金字塔层的尺度不同，设置不同的参数。在较coarse层上，计算亚像素的配准，最小化L2残差，使用大的搜索半径。而在最fine的尺度上，计算像素级的配准，最小化L1残差，使用小的搜索半径。

快速亚像素L2配准

在coarse层上，需要在一个较大的搜索半径内匹配，比较耗时。为了加速配准速度，公式$(1)$可以使用box filter和卷积计算：
$$D_2=\Vert T{\Vert }_2^2+box(I\circ I,n)-2({\mathcal{F}}^{-1}\{\mathcal{F}\{I{\}}^{\ast }\circ \mathcal{F}\{T\}\})\text{\hspace{1em}(2)}$$

上式第一项是$T$中元素的平方和，第二项是$I$中元素的平方被$n\times n$大小(和$T$一样大小)的非归一化box filter卷积，第三项是$I$和$T$的互相关，可以被FFT加速。
通过在整数偏移量$(\hat{u},\hat{v})$附件的$3\times 3$窗口内拟合一个多项式，然后找到多项式的最小值，从而最小化偏移量误差。一般情况下，可以用二次多项式近似：
$$D_2(u,v)\approx \frac{1}{2}[uv]\mathbf{A}[\begin{array}{c}u\\ v\end{array}]+{\mathbf{b}}^T[\begin{array}{c}u\\ v\end{array}]+c\text{\hspace{1em}(3)}$$

其中，$\mathbf{A}$是一个$2\times 2$正定矩阵，$\mathbf{b}$是一个$2\times 1$向量，$c$是一个标量。使用加权最小二乘方法拟合多项式系数，然后可以得到二次多项式的最小值：
$$\mu =-{\mathbf{A}}^{-1}\mathbf{b}\text{\hspace{1em}(4)}$$

$\mu$表示需要加到偏移量$(\hat{u},\hat{v})$上的亚像素位移。

Merging Frames

仅仅做图像全局配准是不够的，因为各帧之间可能存在非刚体变换，场景移动，光线变化等，在做图像融合时还需要把这些因素考虑进去，防止鬼影的出现。对此，文章提出了基于图像对的频域时间滤波的融合方法，将参考图像中的每一个块，与其它每一帧的对应的块进行融合。对于Bayer raw输入的颜色平面使用$16\times 16$的块，而对于特别暗的场景，低频噪声比较剧烈，则使用$32\times 32$大小的块。

噪声模型和块近似

对于Bayer raw数据，噪声是像素独立的，可以用一个简单的信号依赖的形式表达。对于一个信号$x$，噪声方差${\sigma }^2$可以表示为$Ax+B$，其服从泊松分布的形式。参数$A$和$B$仅仅依赖于拍照时模拟和数字增益的设定，可在算法中直接被控制。
为了计算简便，在每个块中，近似噪声是信号无关的，即认为噪声方差在每个块中是一个常数。文章使用每个块中采样值的RMS作为噪声方差的近似值。

鲁棒的基于图像对的时域融合

文章的融合操作是作用于图像块的空间频域的。对于一个给定的参考图像块，从多帧图像中选取其对应的图像块，每帧一块，计算他们各自的2D DFT记为$T_z(\omega )$，其中$\omega =({\omega }_x,{\omega }_y)$。
假设第0帧为参考帧，为了增加对鬼影的鲁棒性，采用了如下的融合方式：
$${\tilde{T}}_0(\omega )=\frac{1}{N}\sum _{z=0}^{N-1}{T}_z(\omega )+A_z(\omega )[T_0(\omega )-T_z(\omega )]\text{\hspace{1em}(5)}$$

对于给定的频率，$A_z$控制着第$z$帧融合进最终结果的程度，其定义为经典的维纳滤波的一种变体：
$$A_z(\omega )=\frac{|D_z(\omega ){|}^2}{|D_z(\omega ){|}^2+c{\sigma }^2}\text{\hspace{1em}(6)}$$

其中，$D_z(\omega )=T_0(\omega )-T_z(\omega )$，噪声方差${\sigma }^2$由噪声模型提供。$c$是一个常数，可以用来调节噪声水平（文章里设为8）。

空间去噪

得到时域滤波结果后，采用如公式$(6)$一样的收缩算子对空间频域稀疏进行空间滤波。通过假设所有$N$帧图像都被做了平均，将空间滤波的噪声方差调节为${\sigma }^2/N$。另外，为了更加符合人眼习惯，设置噪声水平为频率的函数$\tilde{\sigma }=f(\omega )\sigma$，对更高的频率增加噪声水平。

融合Bayer raw图像

对Bayer图像的每一个颜色平面分别用一个局部平移配准，且对准精度不超过像素级。

重叠块

上述的融合操作都是作用于每个空间维度有一半重叠区域的块上的。为了防止出现块边缘的不连续效应，使得融合更加平滑，对块进行窗函数操作。在DFT域使用升余弦函数，对于$0\le x<n$，$\frac{1}{2}-\frac{1}{2}cos(2\pi (x+\frac{1}{2})/n)$，其他区域设为0。

Artifacts

1. 这种滤波方法不能有效地抑制高对比度区域（如强边缘区域）的噪声。这是由于高对比度区域在空间DFT域的分布是非稀疏的，削弱了空间降噪的有效性。
   
2. 由于算法不会拒绝一个不能完全配准的tile，所以有时候会出现轻微的鬼影。
   
3. 有时会出现振铃效应。

Finishing

经过配准和融合之后，拍摄的多帧Bayer raw图像合成单张raw图像，且具有更高的bit深度和SNR。实际中，输入10bit的raw数据会合成12bit的数据。得到输出raw图像后，还需要一系列的ISP后处理流程才能得到可视化RGB图像。这些步骤主要包括：

1. 暗电流扣除
2. 镜头阴影校正
3. 白平衡
4. 去马赛克
5. 彩色去噪
6. 颜色校正
7. 动态范围压缩
8. 去雾
9. 全局色调调整
10. 色差校正
11. 锐化
12. 特定色调颜色调整
13. dithering
    其中，动态范围压缩步骤中，利用获取的短曝光图像以及合成的长曝光图像，采用曝光融合（Mertens 2007）的方式进行曝光融合。曝光融合只在灰度图像上进行，融合后做gamma校正并将原来的颜色赋值上去。

Results

结果在高动态范围场景和暗光场景都能得到不错的结果。

失败的案例

在极端动态范围场景，可能存在过曝光区域。在有快速运动的低光场景，为了避免运动模糊使用较短的曝光时间，可能会残留比较剧烈的噪声。在高对比度场景中，由于使用了曝光融合，可能会存在轻微的中频halos。

参考

google hdr+数据集（需要）：https://hdrplusdata.org/