第2章 Pytorch基础2

链接

2.5 Tensor与Autograd

在神经网络中，一个重要内容就是进行参数学习，而参数学习离不开求导，Pytorch是如何进行求导的呢？
现在大部分深度学习架构都有自动求导的功能，Pytorch也不列外，torch.autograd包就是用来自动求导的。autograd包为张量上所有的操作提供了自动求导功能，而torch.Tensor和torch.Function为autograd上的两个核心类，他们相互连接并生成一个有向非循环图。接下来我们先简单介绍tensor如何实现自动求导，然后介绍计算图，最后用代码实现这些功能。

2.5.1 自动求导要点

autograd包为对tensor进行自动求导，为实现对tensor自动求导，需考虑如下事项：
（1）创建叶子节点(leaf node)的tensor，使用requires_grad参数指定是否记录对其的操作，以便之后利用backward()方法进行梯度求解。requires_grad参数缺省值为False，如果要对其求导需设置为True，与之有依赖关系的节点自动变为True。
（2）可利用requires_grad_()方法修改tensor的requires_grad属性。可以调用.detach()或with torch.no_grad():将不再计算张量的梯度，跟踪张量的历史记录。这点在评估模型、测试模型阶段常常使用。
（3）通过运算创建的tensor（即非叶子节点），会自动被赋于grad_fn属性。该属性表示梯度函数。叶子节点的grad_fn为None。
（4）最后得到的tensor执行backward()函数，此时自动计算各变在量的梯度，并将累加结果保存grad属性中。计算完成后，非叶子节点的梯度自动释放。
（5）backward()函数接受参数，该参数应和调用backward()函数的Tensor的维度相同，或者是可broadcast的维度。如果求导的tensor为标量（即一个数字），backward中参数可省略。
（6）反向传播的中间缓存会被清空，如果需要进行多次反向传播，需要指定backward中的参数retain_graph=True。多次反向传播时，梯度是累加的。
（7）非叶子节点的梯度backward调用后即被清空。
（8）可以通过用torch.no_grad()包裹代码块来阻止autograd去跟踪那些标记为.requesgrad=True的张量的历史记录。这步在测试阶段经常使用。
整个过程中，Pytorch采用计算图的形式进行组织，该计算图为动态图，它的计算图在每次前向传播时，将重新构建。其他深度学习架构，如TensorFlow、Keras一般为静态图。接下来我们介绍计算图，用图的形式来描述就更直观了，该计算图为有向无环图（DAG）。

2.5.2计算图

计算图是一种有向无环图像，用图形方式表示算子与变量之间的关系，直观高效。如图2-8所示，圆形表示变量，矩阵表示算子。如表达式：z=wx+b，可写成两个表示式：$y=wx$，则$z=y+b$，其中$x、w、b$为变量，是用户创建的变量，不依赖于其他变量，故又称为叶子节点。
为计算各叶子节点的梯度，需要把对应的张量参数requires_grad属性设置为True，这样就可自动跟踪其历史记录。y、z是计算得到的变量，非叶子节点，z为根节点。mul和add是算子（或操作或函数）。由这些变量及算子，就构成一个完整的计算过程（或前向传播过程）。

图2-8 正向传播计算图
我们的目标是更新各叶子节点的梯度，根据复合函数导数的链式法则，不难算出各叶子节点的梯度。

Pytorch调用backward()，将自动计算各节点的梯度，这是一个反向传播过程，这个过程可用图2-9表示。在反向传播过程中，autograd沿着图2-9，从当前根节点z反向溯源，利用导数链式法则，计算所有叶子节点的梯度，其梯度值将累加到grad属性中。 对非叶子节点的计算操作（或function）记录在grad_fn属性中，叶子节点的grad_fn值为None。

图2-9 梯度反向传播计算图
下面我们用代码实现这个计算图。

2.5.3 标量反向传播

假设$x、w、b$都是标量，$z=wx+b$，对标量$z$调用backward()，我们无需对backward()传入参数。以下是实现自动求导的主要步骤：
(1)定义叶子节点及算子节点

import torch
 
#定义输入张量x
x=torch.Tensor([2])
#初始化权重参数W,偏移量b、并设置require_grad属性为True，为自动求导
w=torch.randn(1,requires_grad=True)
b=torch.randn(1,requires_grad=True)
#实现前向传播
y=torch.mul(w,x)  #等价于w*x
z=torch.add(y,b)  #等价于y+b
#查看x,w，b页子节点的requite_grad属性
print("x,w,b的require_grad属性分别为：{},{},{}".format(x.requires_grad,w.requires_grad,b.requires_grad))

运行结果
x,w,b的require_grad属性分别为：False,True,True

（2）查看叶子节点、非叶子节点的其他属性

#查看非叶子节点的requres_grad属性,
print("y，z的requires_grad属性分别为：{},{}".format(y.requires_grad,z.requires_grad))
#因与w，b有依赖关系，故y，z的requires_grad属性也是：True,True
#查看各节点是否为叶子节点
print("x，w，b，y，z的是否为叶子节点：{},{},{},{},{}".format(x.is_leaf,w.is_leaf,b.is_leaf,y.is_leaf,z.is_leaf))
#x，w，b，y，z的是否为叶子节点：True,True,True,False,False
#查看叶子节点的grad_fn属性
print("x，w，b的grad_fn属性：{},{},{}".format(x.grad_fn,w.grad_fn,b.grad_fn))
#因x，w，b为用户创建的，为通过其他张量计算得到，故x，w，b的grad_fn属性：None,None,None
#查看非叶子节点的grad_fn属性
print("y，z的是否为叶子节点：{},{}".format(y.grad_fn,z.grad_fn))
#y，z的是否为叶子节点：,

（3）自动求导，实现梯度方向传播，即梯度的反向传播。

#基于z张量进行梯度反向传播,执行backward之后计算图会自动清空，
z.backward()
#如果需要多次使用backward，需要修改参数retain_graph为True，此时梯度是累加的
#z.backward(retain_graph=True)
 
#查看叶子节点的梯度，x是叶子节点但它无需求导，故其梯度为None
print("参数w,b的梯度分别为:{},{},{}".format(w.grad,b.grad,x.grad))
#参数w,b的梯度分别为:tensor([2.]),tensor([1.]),None
 
#非叶子节点的梯度，执行backward之后，会自动清空
print("非叶子节点y,z的梯度分别为:{},{}".format(y.grad,z.grad))
#非叶子节点y,z的梯度分别为:None,None

2.5.4 非标量反向传播

2.5.3小节我们介绍了当目标张量为标量时，调用backward()无需传入参数。目标张量一般是标量，如我们经常使用的损失值Loss，一般都是一个标量。但也有非标量的情况，后面我们介绍的Deep Dream的目标值就是一个含多个元素的张量。如何对非标量进行反向传播呢？Pytorch有个简单的规定，不让张量(tensor)对张量求导，只允许标量对张量求导，因此，如果目标张量对一个非标量调用backward()，需要传入一个gradient参数,该参数也是张量，而且需要与调用backward()的张量形状相同。为什么要传入一个张量gradient？

传入这个参数就是为了把张量对张量求导转换为标量对张量求导。这有点拗口，我们举一个例子来说，假设目标值为$loss=(y_1,y_2,\dots ,y_m)$ 传入的参数为 $v=(v_1,v_2,\dots ,v_m)$ ,那么就可把对loss的求导，转换为对$loss\ast v^T$ 标量的求导。即把原来$\partial loss/\partial x$得到雅可比矩阵(Jacobian)乘以张量$v^T$，便可得到我们需要的梯度矩阵。
backward函数的格式为：

backward(gradient=None, retain_graph=None, create_graph=False)

上面说的可能有点抽象，下面我们通过一个实例进行说明。
（1）定义叶子叶子节点及计算节点

import torch
 
#定义叶子节点张量x，形状为1x2
x= torch.tensor([[2, 3]], dtype=torch.float, requires_grad=True)
#初始化Jacobian矩阵
J= torch.zeros(2 ,2)
#初始化目标张量，形状为1x2
y = torch.zeros(1, 2)
#定义y与x之间的映射关系：
#y1=x1**2+3*x2，y2=x2**2+2*x1
y[0, 0] = x[0, 0] ** 2 + 3 * x[0 ,1]
y[0, 1] = x[0, 1] ** 2 + 2 * x[0, 0]

（2）手工计算y对x的梯度
我们先手工计算一下y对x的梯度，为了验证Pytorch的backward的结果是否正确。
y对x的梯度是一个雅可比矩阵，各项的值，我们可通过以下方法进行计算。

（3）调用backward获取y对x的梯度

y.backward(torch.Tensor([[1, 1]]))
print(x.grad)
# 结果为tensor([[6., 9.]])

这个结果与我们手工运算的不符，显然这个结果是错误的，错在哪里呢？这个结果的计算过程是：

由此，错在v的取值错误，通过这种方式得的到并不是y对x的梯度。这里我们可以分成两步的计算。首先让v=(1,0)得到y_1对x的梯度，然后使v=(0,1)，得到y_2对x的梯度。这里因需要重复使用backward(),需要使参数retain_graph=True,具体代码如下：

#生成y1对x的梯度
y.backward(torch.Tensor([[1, 0]]),retain_graph=True)
J[0]=x.grad
#梯度是累加的，故需要对x的梯度清零
x.grad = torch.zeros_like(x.grad)
#生成y2对x的梯度
y.backward(torch.Tensor([[0, 1]]))
J[1]=x.grad
#显示jacobian矩阵的值
print(J)

运行结果
tensor([[4., 3.],[2., 6.]])
这个结果与手工运行的式（2.5）结果一致。

2.6 使用Numpy实现机器学习

前面我们介绍了Numpy、Tensor的基础内容，对如何用Numpy、Tensor操作数组有了一定认识。为了加深大家对Pytorch是如何进行完成机器学习、深度学习，本章剩余章节将分别用Numpy、Tensor、autograd、nn及optimal实现同一个机器学习任务，比较他们之间的异同及各自优缺点，从而加深对Pytorch的理解。

首先，我们用最原始的Numpy实现有关回归的一个机器学习任务，不用Pytorch中的包或类。这种方法代码可能多一点，但每一步都是透明的，有利于理解每步的工作原理。
主要步骤包括：
首先，是给出一个数组x，然后基于表达式：$y=3x^2+2$，加上一些噪音数据到达另一组数据y。
然后，构建一个机器学习模型，学习表达式 $y=w{x}^2+b$ 的两个参数 $w，b$。利用数组x，y的数据为训练数据
最后，采用梯度梯度下降法，通过多次迭代，学习到 $w、b$ 的值。
以下为具体步骤：
（1）导入需要的库

# -*- coding: utf-8 -*-
import numpy as np
%matplotlib inline
 
from matplotlib import pyplot as plt

（2）生成输入数据x及目标数据y
设置随机数种子，生成同一个份数据，以便用多种方法进行比较。

np.random.seed(100) 
x = np.linspace(-1, 1, 100).reshape(100,1) 
y = 3*np.power(x, 2) +2+ 0.2*np.random.rand(x.size).reshape(100,1) 

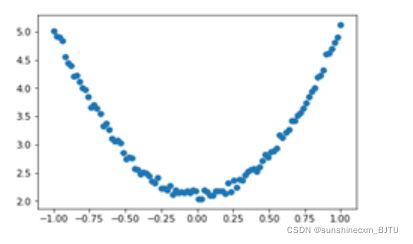
（3）查看x，y数据分布情况

# 画图
plt.scatter(x, y)
plt.show()

图2-10 Numpy实现的源数据
（4）初始化权重参数

# 随机初始化参数
w1 = np.random.rand(1,1)
b1 = np.random.rand(1,1) 

（5）训练模型
定义损失函数，假设批量大小为100：

用代码实现上面这些表达式：

lr =0.001 # 学习率
 
for i in range(800):
    # 前向传播
    y_pred = np.power(x,2)*w1 + b1
    # 定义损失函数
    loss = 0.5 * (y_pred - y) ** 2
    loss = loss.sum()
    #计算梯度
    grad_w=np.sum((y_pred - y)*np.power(x,2))
    grad_b=np.sum((y_pred - y))
    #使用梯度下降法，是loss最小
    w1 -= lr * grad_w
    b1 -= lr * grad_b

（6）可视化结果

plt.plot(x, y_pred,'r-',label='predict')
plt.scatter(x, y,color='blue',marker='o',label='true') # true data
plt.xlim(-1,1)
plt.ylim(2,6)  
plt.legend()
plt.show()
print(w1,b1)

运行结果：

图2-11 可视化Numpy学习结果

[[2.95859544]] [[2.10178594]]
从结果看来，学习效果还是比较理想的。

2.7 使用Tensor及antograd实现机器学习

2.6节可以说是纯手工完成一个机器学习任务，数据用Numpy表示，梯度及学习是自己定义并构建学习模型。这种方法适合于比较简单的情况，如果稍微复杂一些，代码量将几何级增加。是否有更方便的方法呢？这节我们将使用Pytorch的自动求导的一个包antograd，利用这个包及对应的Tensor，便可利用自动反向传播来求梯度，无需手工计算梯度。以下是具体实现代码。
（1）导入需要的库

import torch as t
%matplotlib inline
 
from matplotlib import pyplot as plt

（2）生成训练数据，并可视化数据分布情况

t.manual_seed(100) 
dtype = t.float
#生成x坐标数据，x为tenor，需要把x的形状转换为100x1
x = t.unsqueeze(torch.linspace(-1, 1, 100), dim=1) 
#生成y坐标数据，y为tenor，形状为100x1，另加上一些噪音
y = 3*x.pow(2) +2+ 0.2*torch.rand(x.size())                 
 
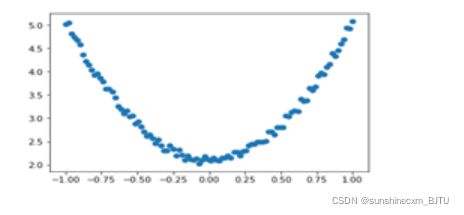
# 画图，把tensor数据转换为numpy数据
plt.scatter(x.numpy(), y.numpy())
plt.show()

图2-12 可视化输入数据
（3）初始化权重参数

# 随机初始化参数，参数w，b为需要学习的，故需requires_grad=True
w = t.randn(1,1, dtype=dtype,requires_grad=True)
b = t.zeros(1,1, dtype=dtype, requires_grad=True) 

（4）训练模型

lr =0.001 # 学习率
 
for ii in range(800):
    # 前向传播，并定义损失函数loss
    y_pred = x.pow(2).mm(w) + b
    loss = 0.5 * (y_pred - y) ** 2
    loss = loss.sum()
    
    # 自动计算梯度，梯度存放在grad属性中
    loss.backward()
    
    # 手动更新参数，需要用torch.no_grad()，使上下文环境中切断自动求导的计算
    with t.no_grad():
        w -= lr * w.grad
        b -= lr * b.grad
    
    # 梯度清零
        w.grad.zero_()
        b.grad.zero_()

（5）可视化训练结果

plt.plot(x.numpy(), y_pred.detach().numpy(),'r-',label='predict')#predict
plt.scatter(x.numpy(), y.numpy(),color='blue',marker='o',label='true') # true data
plt.xlim(-1,1)
plt.ylim(2,6)  
plt.legend()
plt.show()
        
print(w, b)

运行结果：

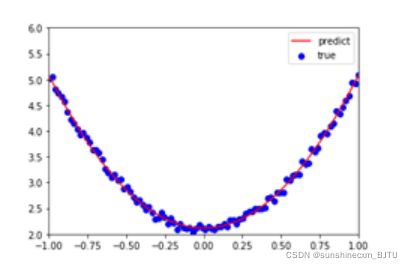
图2-13 使用 antograd的结果
tensor([[2.9645]], requires_grad=True) tensor([[2.1146]], requires_grad=True)
这个结果与使用Numpy机器学习的差不多。