机器学习：集成学习之boosting

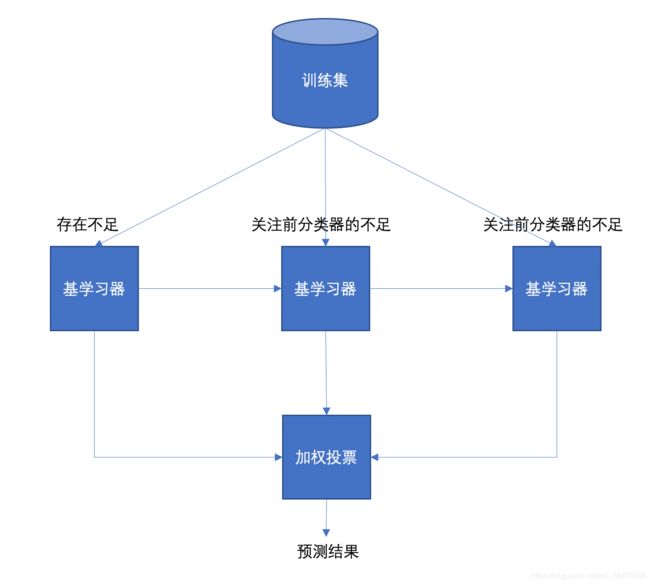
1.Boosting介绍

Boosting体现了提升的思想：

• 每一个训练器重点关注前一个训练器不足的地方进行训练
• 通过加权投票的方法得出最后的预测结果
• 

2.Boosting和Bagging对比

区别一：数据方面

• Boosting：使用的是全部训练样本，根据前一个模型的学习结果调整数据的重要性
• Bagging：对数据进行采样训练

区别二：集成策略

• Bagging：对所有的弱学习器预测的结果进行平权投票，票数较多的最终的强学习器的预测结果。
• Boosting：每一个后边的弱学习器对前一个弱学习器进行加权投票

区别三：学习顺序

• Bagging：并行学习，每一个学习器之间没有依赖关系
• Boosting：串行学习，有先后顺序

3.Adaboost

Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练出不同的基分类器，构成一个更强的强分类器。
基本思想如下：

1、计算样本的权重

• 样本分类正确，降低其样本的权重
• 样本分类错误，提高其样本的权重

2、计算基学习器的错误率

• 错误分类的样本越多，其错误率越高
• 错误分类的样本越少，其错误率越低

3、计算基学习器的权重

• 模型错误率越低，则其权重越大
• 模型错误率越高，则其权重越小

3.1 Adaboost构建过程

1、初始化训练样本权重相等，训练第一个基学习器

• 如果有100个样本，则每一个样本的初始权重都为0.01
• 根据预测结果计算、更新：样本权重和模型权重

2、根据新的权重的样本集训练第二个基学习器

• 根据预测结果计算、更新：样本权重和模型权重

3、迭代训练：在前一个基学习器的基础上，根据新的样本权重训练当前的学习器

4、直至训练出m个基学习器

具体公式如下：
$$H(x)=\mathrm{sign}(\sum _{i=1}^m{\alpha }_i{h}_i(x))$$
公式中，α 为模型的权重，输出结果大于 0 则归为正类，小于 0 则归为负类。

模型权重计算公式：
$${\alpha }_t=\frac{1}{2}\ln (\frac{1-{\epsilon }_t}{{\epsilon }_t})$$
样本权重计算公式：
$$D_{t+1}(x)=\frac{D_t(x)}{Z_t}\ast \{\begin{array}{ll}{e}^{-{\alpha }_t},& \text{ 预测值 }=\text{ 真实值 }\\ e^{{\alpha }_t},& \text{ 预测值 }\ne \text{ 真实值 }\end{array}$$
Z_t 为归一化值（所有样本权重的总和），D_t 为样本权重，α_t 为模型权重。

3.2 Adaboost案例分析

下面为训练数数据，假设弱分类器由 x 产生，其阈值 v 使该分类器在训练数据集上的分类误差率最低，试用 Adaboost 算法学习一个强分类器。

序号	1	2	3	4	5	6	7	8	9	10
x	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1

3.2.1 构建第一棵树

假设我们用决策树作为基学习器：

1、初始化样本的的权重，每一个样本的权重为：0.1
2、构建第一个基学习器：

 1、寻找最优分裂点

1. 对特征值 x 进行排序，确定分裂点为：0.5、1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5
2. 当以 0.5 为分裂点时，有 5 个样本分类错误，错误率是：0.1 * 5=0.5
3. 当以 1.5 为分裂点时，有 4 个样本分类错误，错误率是0.4
4. 当以 2.5 为分裂点时，有 3 个样本分类错误，错误率是0.3
5. 当以 3.5 为分裂点时，有 4 个样本分类错误，错误率是0.4
6. 当以 4.5 为分裂点时，有 5 个样本分类错误，错误率是0.5
7. 当以 5.5 为分裂点时，有 6 个样本分类错误，错误率是：0.1 * 3+0.1 * 3 = 0.6
8. 当以 6.5 为分裂点时，有 5 个样本分类错误，错误率是0.5
9. 当以 7.5 为分裂点时，有 4 个样本分类错误，错误率是0.4
10. 当以 8.5 为分裂点时，有 3 个样本分类错误，错误率是0.3
11. 最终，选择以 2.5 作为分裂点，计算得出基学习器错误率为：0.3

 2、计算模型权重
$${\alpha }_1=\frac{1}{2}\ln (\frac{1-0.3}{0.3})=0.4236$$
 3、更新样本权重

1. 分类正确的样本为：1、2、3、4、5、6、10，其计算公式为：e^-α₁
2. 分类正确样本权重为：e^-0.4236=0.6547
3. 分类错误样本权重为：7、8、9，其计算公式为：e^α₁
4. 分类错误样本权重为：e^0.4236=1.5275
5. 将所有的权重值归一化到0-1范围内 Z₁：0.6547*0.7+1.5275*0.3=0.9165
6. 分类正确样本权重归一化为：
    分类正确样本最终权重为：
   $$D_{2r}=\frac{D_1}{Z_1}\cdot e^{-{\alpha }_1}=\frac{0.1}{0.9165}\times 0.6547=0.07143$$
    分类错误样本最终权重为：
   $$D_{2e}=\frac{D_1}{Z_1}\cdot e^{{\alpha }_1}=\frac{0.1}{0.9165}\times 1.5275=0.1667$$

 4、由此可得基学习器为：

小于2.5

大于2.5

10个样本

3个样本,输出类别:1

7个样本,输出类别:-1

 5、样本更新权重为：

序号	1	2	3	4	5	6	7	8	9	10
x	0	1	2	3	4	5	6	7	8	9
w	0.07143	0.07143	0.07143	0.07143	0.07143	0.07143	0.1667	0.1667	0.1667	0.07143
y	1	1	1	-1	-1	-1	1	1	1	-1

3.2.2 构建第二棵树

 1、寻找最优分裂点

1. 当以 0.5 为分裂点时，有 5 个样本分类错误，错误率为：0.07143 * 2 + 0.16667 * 3 = 0.64287
2. 当以 1.5 为分裂点时，有 4 个样本分类错误，错误率为：0.07143 * 1 + 0.16667 * 3 = 0.57144
3. 当以 2.5 为分裂点时，有 3 个样本分类错误，错误率为：0.16667 * 3 = 0.57144 = 0.5
4. 当以 3.5 为分裂点时，有 4 个样本分类错误，错误率为：0.07143 * 1 + 0.16667 * 3 = 0.57144
5. 当以 4.5 为分裂点时，有 5 个样本分类错误，错误率为：0.07143 * 2 + 0.16667 * 3 = 0.64287
6. 当以 5.5 为分裂点时，有 6 个样本分类错误，错误率为：0.07143 * 3 + 0.16667 * 3 = 0.7143
7. 当以 6.5 为分裂点时，有 5 个样本分类错误，错误率为：0.07143 * 3 + 0.16667 * 2 = 0.54763
8. 当以 7.5 为分裂点时，有 4 个样本分类错误，错误率为：0.07143 * 3 + 0.16667 * 1 = 0.38096
9. 当以 8.5 为分裂点时，有 3 个样本分类错误，错误率为：0.07143 * 3 = 0.21429
10. 最终，选择以 8.5 作为分裂点，计算得出基学习器错误率为：0.21429

 2、计算模型权重
$${\alpha }_2=\frac{1}{2}\cdot \ln (\frac{1-0.21429}{0.21429})=0.64963$$
 3、更新样本权重

1. 分类正确的样本为：1、2、3、7、8、9、10，其计算公式为：e^-α₂
2. 分类正确样本权重为：e^-0.64963=0.52224
3. 分类错误样本权重为：4、5、6，其计算公式为：e^α₂
4. 分类错误样本权重为：e^0.64963=1.91483
5. 将所有的权重值归一化到0-1范围内 Z₂：0.07143 * 0.52224 * 4 + 0.16667 * 0.52224 * 3+ 0.07143 * 1.91483 * 3= 0.82067
6. 分类正确样本权重归一化为：
    分类正确样本最终权重为：
   $$D_{3r}=\frac{D_{2r}}{Z_2}\cdot e^{-{\alpha }_2}=\frac{0.07143}{0.82067}\times 0.52224=0.0455$$
   $$D_{3r}=\frac{D_{2r}}{Z_2}\cdot e^{-{\alpha }_2}=\frac{0.16667}{0.82067}\times 0.52224=0.1061$$
    分类错误样本最终权重为：
   $$D_{3e}=\frac{D_{2e}}{Z_2}\cdot e^{{\alpha }_2}=\frac{0.07143}{0.82067}\times 1.91483=0.16667$$

 4、由此可得基学习器为：

小于8.5

大于8.5

10个样本

9个样本,输出类别:1

1个样本,输出类别:-1

 5、样本更新权重为：

序号	1	2	3	4	5	6	7	8	9	10
x	0	1	2	3	4	5	6	7	8	9
w	0.0455	0.0455	0.0455	0.16667	0.16667	0.16667	0.1061	0.1061	0.1061	0.0455
y	1	1	1	-1	-1	-1	1	1	1	-1

3.2.3 构建第三棵树

 1、寻找最优分裂点：通过调整特征权重以后，发现目标值为-1的特征值权重占比较大，说明目标值为-1的样本容易分错，建立第三棵树时重点关注分错特征值。

1. 当以 0.5 为分裂点时，有 5 个样本分类错误，错误率为：0.0455 * 1 + 0.16667 * 3 + 0.0455 * 1= 0.59101
2. 当以 1.5 为分裂点时，有 4 个样本分类错误，错误率为：0.0455 * 2 + 0.16667 * 3 + 0.0455 * 1 = 0.63651
3. 当以 2.5 为分裂点时，有 3 个样本分类错误，错误率为：0.0455 * 3 + 0.16667 * 3 + 0.0455 * 1 = 0.68201
4. 当以 3.5 为分裂点时，有 4 个样本分类错误，错误率为：0.0455 * 3 + 0.16667 * 2 + 0.0455 * 1 = 0.51534
5. 当以 4.5 为分裂点时，有 5 个样本分类错误，错误率为：0.0455 * 3 + 0.16667 * 1 + 0.0455 * 1 = 0.34867
6. 当以 5.5 为分裂点时，有 6 个样本分类错误，错误率为：0.0455 * 3 + 0.16667 * 0 + 0.0455 * 1 = 0.182
7. 当以 6.5 为分裂点时，有 5 个样本分类错误，错误率为：0.0455 * 3 + 0.1061 * 1 + 0.0455 * 1 = 0.2881
8. 当以 7.5 为分裂点时，有 4 个样本分类错误，错误率为：0.0455 * 3 + 0.1061 * 2 + 0.0455 * 1 = 0.3942
9. 当以 8.5 为分裂点时，有 3 个样本分类错误，错误率为：0.0455 * 3 + 0.1061 * 3 + 0.0455 * 1 = 0.5003
10. 最终，选择以 5.5 作为分裂点，计算得出基学习器错误率为：0.182

 2、计算模型权重
$${\alpha }_3=\frac{1}{2}\cdot \ln (\frac{1-0.182}{0.182})=0.7514$$

 3、更新样本权重

1. 分类正确的样本为：4、5、6、7、8、9，其计算公式为：e^-α₃
2. 分类正确样本权重为：e^-0.7514=0.4717
3. 分类错误样本权重为：1、2、3、10，其计算公式为：e^α₃
4. 分类错误样本权重为：e^0.7514=2.11997
5. 将所有的权重值归一化到0-1范围内 Z₃：0.0455 * 2.11997 * 3 + 0.0455 * 2.11997 * 1 + 0.16667 * 0.4717 * 3 + 0.1061 * 0.4717 * 3= 0.77183
6. 分类正确样本权重归一化为：
    分类正确样本最终权重为：
   $$D_{4r}=\frac{D_{3r}}{Z_3}\cdot e^{-{\alpha }_3}=\frac{0.16667}{0.77183}\times 0.4717=0.10185$$
   $$D_{4r}=\frac{D_{3r}}{Z_3}\cdot e^{-{\alpha }_3}=\frac{0.1061}{0.77183}\times 0.4717=0.06484$$
    分类错误样本最终权重为：
   $$D_{4e}=\frac{D_{3e}}{Z_2}\cdot e^{{\alpha }_3}=\frac{0.0455}{0.77183}\times 2.11997=0.12497$$

 4、由此可得基学习器为：

小于5.5

大于5.5

10个样本

6个样本,输出类别:-1

4个样本,输出类别:1

 5、样本更新权重为：

序号	1	2	3	4	5	6	7	8	9	10
x	0	1	2	3	4	5	6	7	8	9
w	0.12497	0.12497	0.12497	0.06484	0.06484	0.06484	0.06484	0.06484	0.06484	0.12497
y	1	1	1	-1	-1	-1	1	1	1	-1

依次迭代更新到n棵树：

3.2.4 最终强学习器

假设：我们只构建 3 棵决策树，此时我们的模型如下：

小于2.5

大于2.5

小于8.5

大于8.5

小于5.5

大于5.5

10个样本

3个样本,输出类别:1

7个样本,输出类别:-1

10个样本

9个样本,输出类别:1

1个样本,输出类别:-1

10个样本

6个样本,输出类别:-1

4个样本,输出类别:1

此时得到强学习器：
$$\mathrm{H}(x)=\mathrm{sign}\left(0.4236\ast h_1(x)+0.64963\ast h_2(x)+0.7514\ast h_3(x)\right)$$

1. 如果 H(x) 的值大于 0 则归为正类
2. 如果 H(x) 的值小于 0 则归为负类

3.2.5 验证强学习器

取样本6为例：

• 代入第一个弱学习器，输出-1
• 代入第二个弱学习器，输出1
• 代入第三个弱学习器，输出1
  $$\mathrm{H}(x)=\mathrm{sign}\left(0.4236\times (-1)+0.64963\times 1+0.7514\times 1\right)=\mathrm{sign}(0.97743)$$

4.GBDT

4.1 GBDT基本概念

概念：

GBDT 的全称是 Gradient Boosting Decision Tree，梯度提升决策树，简称梯度提升树。

1. GBDT 使用 CART 回归树
2. CART 回归树使用平方误差

4.2 提升树

提升树的基本思想去拟合残差。

案例分析：

x	1	2	3	4	5	6	7	8	9	10
目标值	5.56	5.70	5.91	6.40	6.80	7.05	8.90	8.70	9.00	9.05

4.2.1 构建第一棵树

1、计算训练数据的最优切分点，及平方损失

切分点	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
平方误差	15.72	12.07	8.36	5.78	3.91	1.93	8.01	11.73	15.74

计算每一个划分点的平方损失，例如：1.5 的平方损失计算过程为：

1. R1 为 小于 1.5 的样本个数，样本数量为：1，其输出值为：5.56
   $$\begin{array}{l}R1=5.56\end{array}$$

2. R2 为 大于 1.5 的样本个数，样本数量为：9 ，其输出值为：
   $$\begin{array}{l}R2=(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)/9=7.50\end{array}$$

3. 该划分点的平方损失：
   $$L(1.5)=(5.56-5.56{)}^2+\left[(5.7-7.5{)}^2+(5.91-7.5{)}^2+\dots +(9.05-7.5{)}^2\right]=0+15.72=15.72$$

其他划分点的平方损失同上。

2、当 6.5 作为切分点时，平方损失最小，此时得到第一棵决策树：

小于6.5

大于6.5

10个样本

6个样本, 输出: 6.24

4个样本, 输出: 8.91

• 该树左子树的输出值为：(5.56 + 5.70 + 5.91 + 6.40 + 6.80 + 7.05) / 6 ≈ 6.24

• 该树右子树的输出值为：(8.90 + 8.70 + 9.00 + 9.05) / 4 ≈ 8.91

4.2.2 构建第二棵树

1、残差表如下：

x	1	2	3	4	5	6	7	8	9	10
目标值	5.56	5.70	5.91	6.40	6.80	7.05	8.90	8.70	9.00	9.05
预测值	6.24	6.24	6.24	6.24	6.24	6.24	8.91	8.91	8.91	8.91
残差	-0.68	-0.54	-0.33	0.16	0.56	0.81	-0.01	-0.21	0.09	0.14

2、以残差为目标值，拟合残差，进行二次构建CART树

x	1	2	3	4	5	6	7	8	9	10
目标值	-0.68	-0.54	-0.33	0.16	0.56	0.81	-0.01	-0.21	0.09	0.14

3、找出最优切分点，计算每一个切分点的平方损失（同过程一计算切分点）

切分点	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
平方损失	1.42	1.0	0.79	1.13	1.66	1.93	1.93	1.9	1.91

4、以3.5为切分点时，平方损失最小，此时得到的二叉决策树为：

小于3.5

大于3.5

10个样本

3个样本, 输出: -0.52

7个样本, 输出: 0.22

• 该树左子树的输出值为：(-0.68-0.54-0.33) / 3 ≈ 0.52

• 该树右子树的输出值为：(0.16+0.56+0.81+(-0.01)+(-0.21)+0.09+0.14) / 7 ≈ 0.22

4.2.3 构建第三棵树

1. 残差表如下：

x	1	2	3	4	5	6	7	8	9	10
目标值	-0.68	-0.54	-0.33	0.16	0.56	0.81	-0.01	-0.21	0.09	0.14
预测值	-0.52	-0.52	-0.52	0.22	0.22	0.22	0.22	0.22	0.22	0.22
残差	-0.16	-0.02	0.21	-0.06	0.34	0.57	-0.23	-0.43	-0.13	-0.08

2、以残差为目标值，拟合残差，进行三次构建CART树

x	1	2	3	4	5	6	7	8	9	10
目标值	0.16	-0.02	0.21	-0.06	0.34	0.57	-0.23	-0.43	-0.13	-0.08

3、找出最优切分点，计算每一个切分点的平方损失

切分点	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
平方损失	1.34	1.35	1.29	1.31	1.4	1.26	1.32	1.4	1.4

4、当 6.5 作为切分点时，平方损失最小，此时得到第二棵决策树：

小于6.5

大于6.5

10个样本

6个样本, 输出: 0.15

4个样本, 输出: -0.22

• 该树左子树的输出值为：(0.16+(-0.02)+0.21+(-0.06)+0.34+0.57) / 6 ≈ 0.15

• 该树右子树的输出值为：(-0.23-0.43-0.13-0.08) / 4 ≈ -0.22

4.2.4 最终强学习器

假设：我们只构建 3 棵决策树，此时我们的模型如下：

小于6.5

大于6.5

小于3.5

大于3.5

小于6.5

大于6.5

10个样本

6个样本, 输出: 6.24

4个样本, 输出: 8.91

10个样本

3个样本, 输出: -0.52

7个样本, 输出: 0.22

10个样本

6个样本, 输出: 0.15

4个样本, 输出: -0.22

x	1	2	3	4	5	6	7	8	9	10
目标值	5.56	5.70	5.91	6.40	6.80	7.05	8.90	8.70	9.00	9.05
预测值	5.87	5.87	5.87	6.61	6.61	6.61	8.91	8.91	8.91	8.91

模型的总的平方误差为：0.47

(5.56 - 5.87)**2 + (5.70-5.87)**2 + (5.91-5.87)**2 + (6.40-6.61)**2 + (6.80-6.61)**2 + (7.05-6.61)**2 + (8.90-8.91)**2 + (8.70-8.91)**2 + (9-8.91)**2 + (9.05-8.91)**2 = 0.47

如果我们继续构增加基学习器到 6 个，那么平方误差会从 0.47 降低到 0.17。该树模型即为提升树。

4.3 梯度提升树

梯度提升树的基本思想是拟合负梯度

提升树使用加法模型和前向分布算法实现学习的优化过程。

x	1	2	3	4	5	6	7	8	9	10
目标值	5.56	5.70	5.91	6.40	6.80	7.05	8.90	8.70	9.00	9.05

4.3.1 初始化树

我们通过计算当模型预测值为何值时，会使得第一个基学习器的平方误差最小，即：求损失函数对 f(x_i) 的导数，并令导数为0.

$$L(y,f(x))=\frac{1}{2}\sum _{i=1}^n(y_i-f(x_i){)}^2$$
$$\frac{\partial L(y,f(x_i))}{\partial f(x_i)}=\sum _{i=1}^n(y-f(x_i))=0=>\sum _{i=1}^n{y}_i-\sum _{i=1}^{n}f(x_i)=0=>f(x_i)=(\sum _{i=1}^n{y}_i)/n$$
将样本代入上述公式，此时得到初始化基学习器为：

10个样本, 输出值: 7.31

4.3.2 构建第一棵树

由于我们拟合的是样本的负梯度，即：

$$\frac{\partial L(y,f(x_i))}{\partial f(x_i)}=f(x_i)-y_i$$
$$-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}]=y_i-f(x_i)$$

1、负梯度表如下：

x	1	2	3	4	5	6	7	8	9	10
目标值	5.56	5.70	5.91	6.40	6.80	7.05	8.90	8.70	9.00	9.05
预测值	7.31	7.31	7.31	7.31	7.31	7.31	7.31	7.31	7.31	7.31
负梯度	-1.75	-1.61	-1.40	-0.91	-0.51	-0.26	1.59	1.39	1.69	1.74

切分点	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
平方损失	15.72	12.08	8.37	5.78	3.91	1.93	8.01	11.74	15.74

2、以 6.5 作为切分点损失最小，构建决策树如下：

小于6.5

大于6.5

10个样本

6个样本, 输出: -1.07

4个样本, 输出: 1.60

4.3.3 构建第二棵树

x	1	2	3	4	5	6	7	8	9	10
目标值	-1.75	-1.61	-1.40	-0.91	-0.51	-0.26	1.59	1.39	1.69	1.74
预测值	-1.07	-1.07	-1.07	-1.07	-1.07	-1.07	1.60	1.60	1.60	1.60
负梯度	-0.68	-0.54	-0.33	0.16	0.56	0.81	-0.01	-0.21	0.09	0.14

切分点	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
平方损失	1.42	1.00	0.79	1.13	1.66	1.93	1.93	1.9	1.91

以 3.5 作为切分点损失最小，构建决策树如下：

小于3.5

大于3.5

10个样本

3个样本, 输出: -0.52

7个样本, 输出: 0.22

4.3.4 构建第三棵树

x	1	2	3	4	5	6	7	8	9	10
目标值	-0.68	-0.54	-0.33	0.16	0.56	0.81	-0.01	-0.21	0.09	0.14
预测值	-0.52	-0.52	-0.52	0.22	0.22	0.22	0.22	0.22	0.22	0.22
负梯度	-0.16	-0.02	0.19	-0.06	0.34	0.59	-0.23	-0.43	-0.13	-0.08

切分点	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
平方损失	0.76	0.77	0.79	0.79	0.76	0.47	0.59	0.76	0.78

以 6.5 作为切分点损失最小，构建决策树如下：

小于6.5

大于6.5

10个样本

6个样本, 输出: 0.15

4个样本, 输出: -0.22

4.3.5 最终强学习器

假设：我们只构建 4 棵决策树，此时我们的模型如下：

小于6.5

大于6.5

小于3.5

大于3.5

小于6.5

大于6.5

10个样本, 输出值: 7.31

10个样本

6个样本, 输出: -1.07

4个样本, 输出: 1.60

10个样本

3个样本, 输出: -0.52

7个样本, 输出: 0.22

10个样本

6个样本, 输出: 0.15

4个样本, 输出: -0.22

x	1	2	3	4	5	6	7	8	9	10
目标值	5.56	5.70	5.91	6.40	6.80	7.05	8.90	8.70	9.00	9.05
预测值	5.87	5.87	5.87	6.61	6.61	6.61	8.91	8.91	8.91	8.91

4.3.6 GBDT总结

残差：

  一个样本真实值与预测值之间的差距。当我们知道损失函数时，残差计算可以用下面的过程来计算：

1. 计算损失函数的负梯度
2. 将某个样本代入负梯度的公式中，得出的结果即为残差
3. 所以，拟合残差也叫做拟合负梯度

算法流程:

1. 初始化弱学习器
2. 迭代构建学习器，每一个学习器拟合上一个学习器的负梯度
3. 直到达到指定的学习器个数
4. 当输入未知样本时，将所有弱学习器的输出结果加起来作为强学习器的输出

学习率:

1. 学习率用来平衡树的数量、每棵树的贡献，学习率可以抵抗过拟合，通过调整学习率的大小调整树的贡献程度
2. 学习率越小，每棵树的贡献就越小，需要更多的树提高精度
3. 学习率越大，每棵树的贡献就越大，需要树的数量就越少
4. 一般情况下为了防止过拟合，提高模型的泛化性能，通过调整学习率，让模型对于训练集的拟合效果不那么高，降低对训练集的依赖性。