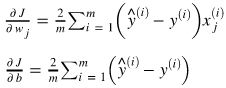线性回归算法python实现_用python实现线性回归算法

本文是根据https://blog.csdn.net/dqcfkyqdxym3f8rb0/article/details/79767043这篇博客写出来的。其中的公式什么的能够去这个博客里面看。

本文主要讲述的是关于其中的线性回归算法中每一段的意思，以供本身之后参考学习。web

import numpy as np #引入numpy科学计算库

import matplotlib.pyplot as plt #引入绘图库

from sklearn.model_selection import train_test_split#从sklearn里面引出训练与测试集划分

np.random.seed(123) #随机数生成种子

x=2*np.random.rand(500,1)#随机生成一个0-2之间的，大小为(500，1)的向量

y=5+3*x+np.random.randn(500,1)#随机生成一个线性方程的，大小为(500，1)的向量

fig=plt.figure(figsize=(8,6))#肯定画布大小

plt.scatter(x,y)#设置为散点图

plt.title("Dataset")#标题名

plt.xlabel("First feature")#x轴的标题

plt.ylabel("Second feature")#y轴的标题

plt.show()#绘制出来

经过观察此图，能够发现x轴的大小限制在0-2之间，而y则是根据是那上面的线性方程y=5+3*x+n，这个n是一个呈正态分布的随机量。

上面的一切都是在随机生成数据，为的就是可以本身生成一个小型的数据集。算法

x_train,x_test,y_train,y_test=train_test_split(x,y)#将上面获得的数据集进行划分，按照3：1的比例分给训练集

#和测试集

print(f'Shape x_train:{x_train.shape}')#输出x轴训练集的大小

print(f'Shape y_train:{y_train.shape}')#同上

print(f'Shape x_test:{x_test.shape}')#同上

print(f'Shape y_test:{y_test.shape}')#同上

Shape x_train:(375, 1)

Shape y_train:(375, 1)

Shape x_test:(125, 1)

Shape y_test:(125, 1)数组

上面的数据就是上一代码块所能获得输出。今后咱们能够看出，数据集已经成功按照3：1的比例分红了训练集和测试集。

如今开始写线性回归的类：app

class LinearRegression:#类名

def _init_(self):#初始化

pass#什么也不作，只是单纯的防止语句错误

def train_gradient_descent(self,x,y,learning_rate=0.01,n_iters=100):#梯度降低法训练，x，y不用解释，

#学习率就是学习的速度，n_iters是迭代的次数

n_samples,n_features=x.shape#将x的大小x=500，y=1分别分给样品和特征

self.weights=np.zeros(shape=(n_features,1))#如下都是第零步，给权值赋为0,这里的n_features==1

self.bias=0#误差赋值为0

costs=[]#申请一个损失数组

for i in range(n_iters):#迭代n_iters次

y_predict=np.dot(x,self.weights)+self.bias#第一步：y_predict=X*w+b

cost=(1/n_samples)*np.sum((y_predict-y)**2)#第二步，得训练集的损失

costs.append(cost)#将损失加到损失数组里面

if i%100==0:#每过一百次输出一下损失

print(f"Cost at iteration{i}:{cost}")

dJ_dw=(2/n_samples)*np.dot(x.T,(y_predict-y))#第三步 第一个公式，得对应偏导数的梯度

dJ_db=(2/n_samples)*np.sum((y_predict-y))#第三步 第二个公式

self.weights=self.weights-learning_rate*dJ_dw#第四步 第一个公式，刷新权值

self.bias=self.bias-learning_rate*dJ_db#第四步 第二个公式，刷新误差

return self.weights,self.bias,costs#返回所得参数

def train_normal_equation(self,x,y):#正规的方程训练

self.weights=np.dot(np.dot(np.linalg.inv(np.dot(x.T,x)),x.T),y)#正规方程公式

self.bias=0

return self.weights,self.bias

def predict(self,x):

return np.dot(x,self.weights)+self.bias

如下步骤，皆属于复制的置顶博客中的 步骤

a) 梯度降低法dom

第 0 步：svg

用0 (或小的随机值)来初始化权重向量和偏置量，或者直接使用正态方程计算模型参数函数

第 1 步(只有在使用梯度降低法训练时须要)：学习

计算输入的特征与权重值的线性组合，这能够经过矢量化和矢量传播来对全部训练样本进行处理：

测试

其中 X 是全部训练样本的维度矩阵，其形式为

；· 表示点积。.net

第 2 步(只有在使用梯度降低法训练时须要)：

用均方偏差计算训练集上的损失：

第 3 步(只有在使用梯度降低法训练时须要):

对每一个参数，计算其对损失函数的偏导数：

全部偏导数的梯度计算以下：

第 4 步(只有在使用梯度降低法训练时须要):

更新权重向量和偏置量：

其中，表示学习率。

b) 正态方程(封闭形式解)：

其中 X 是一个矩阵，其形式为

，包含全部训练样本的维度信息。

regressor=LinearRegression() #梯度降低法的一个实例化对象

w_trained,b_trained,costs=regressor.train_gradient_descent(x_train,y_train,learning_rate=0.005,n_iters=600)

#对该对象进行训练，并获取训练以后的权值与误差

fig=plt.figure(figsize=(8,6))#设置画布大小

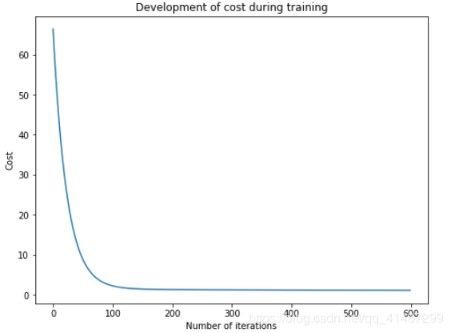
plt.plot(np.arange(600),costs)#设置绘画内容，x轴为迭代次数，y轴为训练集的损失

plt.title("Development of cost during training")#标题

plt.xlabel("Numbers of iterations: ")#x轴标题

plt.ylabel("Cost")#y轴标题

plt.show()#显示

n_samples,_=X_train.shape#这里想要的只有训练集的行数，_表明的也是一个变量名，只是为1，为何用

#至关于被抛弃的那种。之因此写在这里，也是为了防止程序出错

n_samples_test,_=X_test.shape#这里想要的是测试集的行数

y_p_train=regressor.predict(X_train)#计算训练集中的特征与权值的线性组合，借鉴梯度降低法中的第一步

y_p_test=regressor.predict(X_test)#计算测试集中的特征与权值的线性组合

error_train=(1/n_samples)*np.sum((y_p_train-y_train)**2)#这里计算的是训练集的的偏差

error_test=(1/n_samples_test)*np.sum((y_p_test-y_test)**2)#这里计算的是测试集的的偏差

print(f"error on training set:{np.round(error_train,4)}")#输出训练集的偏差，保留四位小数

print(f"error on testing set:{np.round(error_test)}")#输出测试集的偏差

Error on training set: 1.0955

Error on test set: 1.0

以上为上代码块的输出。

X_b_train=np.c_[np.ones(n_samples),X_train]#按行进行组合两个矩阵,组合以后的矩阵大小为(375，2)

X_b_test=np.c_[np.ones(n_samples_test),X_test]#按行进行组合两个矩阵,,组合以后的矩阵大小为(125，2)

reg_normal=LinearRegression()#创建一个使用正态方程的实例化对象

w_trained=reg_normal.train_normal_equation(X_b_train,y_train)#使用了正态方程训练以后的权值

以上代码块是正态方程的训练。

y_p_train=reg_normal.predict(X_b_train)#计算正态训练集中的特征与权值的线性组合，借鉴梯度降低法中的第一步

y_p_test=reg_normal.predict(X_b_test)#计算正态测试集中的特征与权值的线性组合

error_train=(1/n_samples)*np.sum((y_p_train-y_train)**2)#下面这四个我就不赘述了！解释就在前面的代码块中

error_test=(1/n_samples_test)*np.sum((y_p_test-y_test)**2)

print(f"Error on training set:{np.round(error_train,4)}")

print(f"Error on test set:{np.round(error_test,4)}")

Error on training set: 1.0228

Error on test set: 1.0432

以上是上面代码块的输出。

fig=plt.figure(figsize=(8,6))#设置画布大小

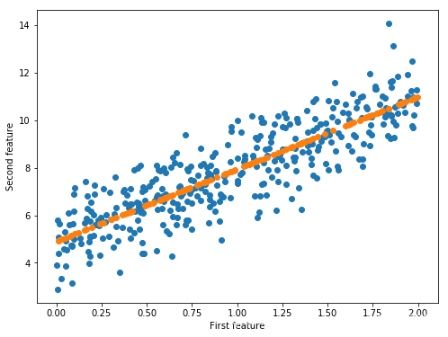
plt.scatter(X_train,y_train)#绘制训练集的散点图

plt.scatter(X_test,y_p_test)#绘制测试集的散点图，注意这里的y_p_test是正态以后的测试集的y

plt.xlabel("First feature")#x轴的标题

plt.ylabel("Second feature")#y轴的标题

plt.show()#显示

完结撒花！