2022美赛C题-交易策略 解析与代码
第一步 题目解析
将题目简单叙述就是：
黄金和比特币是两种波动性资产，题目给了我们两个csv文件，分别存放了黄金和比特币过去几年的价格。我们需要开发一个模型，该模型使用过去每日的价格数据来确定今天如何进行资产交易。
题中的关键信息是：
- 我们这次比赛只能使用这两个csv数据文件解决问题（不能找其他数据）
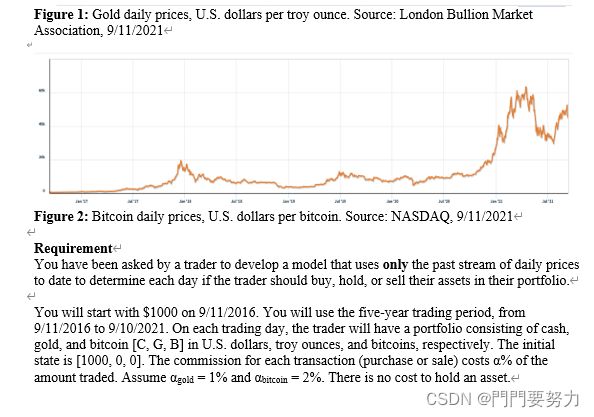
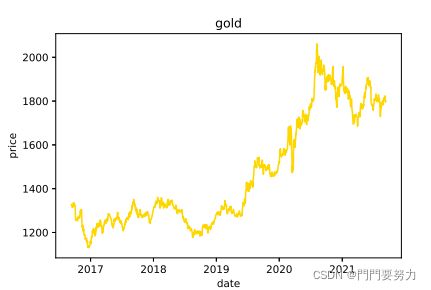
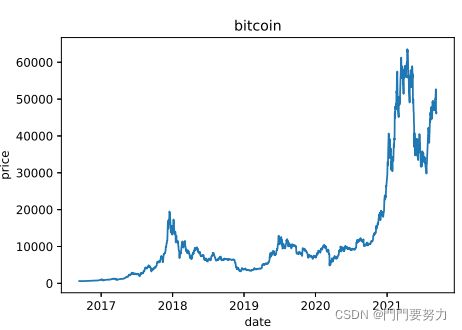
- 数据的日期范围是2016年9月11日-2021年9月10日，起始资金为1000美元现金，资产组合形式为 [现金，黄金，比特币]
- 构建的模型仅使用迄今为止过去的每日价格流来确定交易策略。
即，假设我已构建好模型y = Trade(x)，那么在2017年2月22日这天使用模型时，模型的输入参数x只能是2017.02.22这天及之前的数据，输出是今天应该卖出1个比特币，买入1盎司黄金 - 每笔交易都有佣金成本，交易金额的α%。α黄金= 1%，α比特币= 2%（第三问提到成本对模型的影响）
- 比特币每天可交易，但黄金只在市场开放的日子交易。在csv文件中也能看出黄金的数据有缺失（周末和圣诞节等节假日）
第二步 数据预处理
由于黄金的数据有缺失，在后续数据分析中可能造成影响，我们可以将缺失的价格填充，使用缺失日前后的价格填充缺失的价格。这样的话相当于在非交易日期黄金的价格是不变的，在构建价格预测模型时更加准确，也少很多bug（我当时就苦于某些日期无法预测价格的麻烦）。
# 读取csv文件，指定时间为行索引
df = pd.read_csv('path',index_col='Date')
# 将行索引的时间改为pandas的时间类型
df.index = pd.to_datetime(df.index)
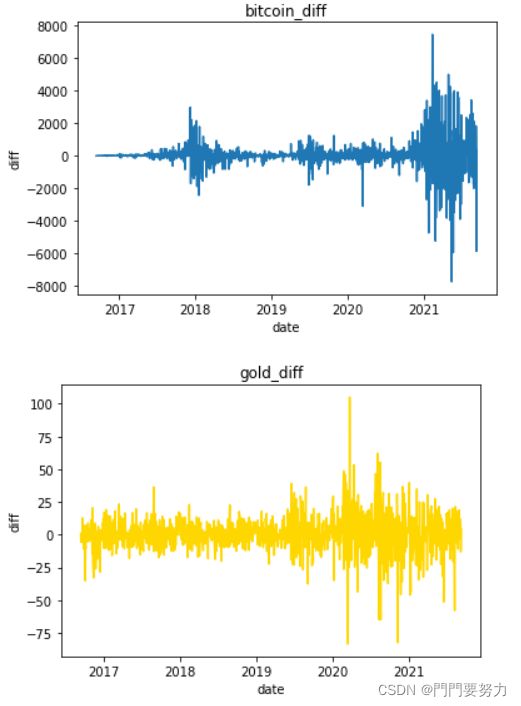
# 产生一阶差分的函数
df['value'].diff(1)
# 填充缺失值
date_index = pd.date_range('2016-09-11','2021-09-10') #先产生所有日期范围
df = df.reindex(date_index) #重设行索引为所有日期
# 此时的dataframe中会将原本有的日期价格填入，而此前没有的日期的价格为NaN缺失
# 使用后一天的价格填充缺失值
gold_df = gold_df.fillna(method='bfill')
当然还有很多其他需要处理的地方……
第三步 构建价格预测模型
时间序列ARIMA(p,d,q)模型学习
1.模型介绍
该模型要求样本具有平稳性
1. 平稳性：要求由样本时间序列所得的拟合曲线在未来一段时间内仍按照现有i形态的“惯性”延续下去。（均值方差无明显变化）
·严平稳：分布不随时间改变而变化
·弱平稳：期望与相关系数（依赖性）不变。未来时刻值与过去信息相关
2. 差分法：时间序列在t与t-1时刻的差值
·一阶差分：在原始数据上使用pandas.diff函数求前后相邻差
·二阶差分：在一阶差分的数据上做差分
3. 自回归模型(AR)
描述当前值与历史值之间的关系，用变量的历史时间数据对自身进行预测
p阶表示当前天与前p天数据有关
4. 移动平均模型（MA）
关注AR模型中误差项的累加，消除预测中的随机波动
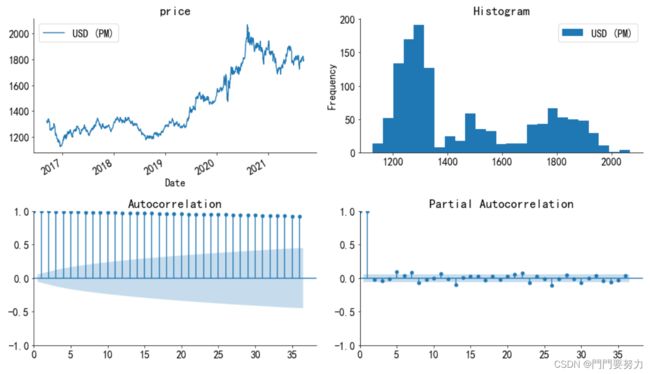
2.参数设置
1. 自相关函数ACF
2. 偏自相关函数PACF： 剔除其他随机变量的影响
ARIMA建模流程：
1.将序列平稳：差分法确定d
2.p和q阶数的确定：acf与pacf
3.ARIMA(p,d,q)
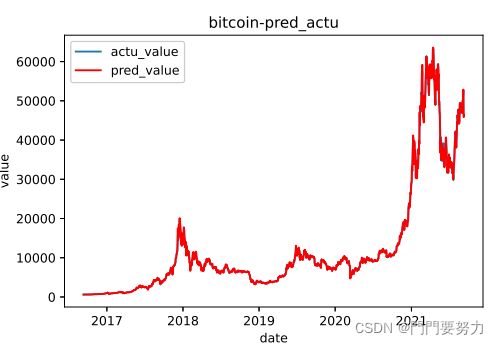
# 根据历史预测today价格的函数
def pred_by_history(df):
model = ARIMA(df[:-1], order=(1, 1, 0)) #只使用today之前的数据建立模型
result = model.fit()
# future = result.predict(df.index[-1],df.index[-1] ,dynamic=True, typ='levels') #预测today的gold价格,起始数据必须在源数据中
future = result.forecast(1) #返回today的预测值
return future
pred_all_gold = {} #字典中存放所有的黄金预测价格
# 一天一天的预测，每次预测传的数据是今天之前的，返回的是今天的预测值
for today in gold_df['2016-09-14':].index.to_list():
pred_gold = pred_by_history(gold_df[:today]) #只使用today之前的数据，返回的是today的预测值
pred_all_gold[today] = pred_gold[0]
print(today)
第四步 构建交易策略模型
使用过去的价格涨跌幅的中位数，九分位数……作为参数
df['change'] = df.value.diff() #相对于昨天涨跌幅
df['ratio'] = df.change / df.value #涨跌比率
df['up'] = df.ratio[df.ratio > 0]
df['down'] = df.ratio[df.ratio < 0]
up_05 = df.up.quantile(.5) #涨幅中位数0.015516689495233852
up_u = 4
up_09 = 0.177859096 #最大累计涨幅
模型输入参数为今天的价格，过去的涨跌幅中位数，九分位数，累积涨跌天数，α第一天买卖额。
输出为今天的买/卖额
def model(P1,M05,M01,α,U1=4):
list1 = [ M05*(1+M01/U1)*(1-α)+(1-α)*M01/U1-α ,M05*(1-α)-α,0,0]
list2 =[ M05*(1-α)*(1+M01/U1)**2+(1-α)*(2+M01/U1)*M01/U1-α,M05*(1+M01/U1)*(1-α)+(1-α)*M01/U1-α ,M05*(1-α)-α,0]
list3 =[ M05*(1-α)*(1+M01/U1)**3+(1-α)*(M01/U1)*(1+(1+M01/U1)**2)-α,M05*(1-α)*(1+M01/U1)**2+(1-α)*(2+M01/U1)*M01/U1-α,M05*(1+M01/U1)*(1-α)+(1-α)*M01/U1-α ,M05*(1-α)-α]
list_all = [list1,list2,list3]
a =np.mat([i[1:] for i in list_all])#系数矩阵
b =np.mat([i[0] for i in list_all]).T #常数项列矩阵
P=solve(a,b) #方程组的解
print(P1,P[0],P[1],P[2])
# [[436.40492024]
# [560.68906005]]
from scipy.optimize import curve_fit #拟合求参数
def y(a,t):
return a*np.exp(t)
x = [i for i in range(1,5)] #x=np.linspace(1,4,4)
popt, pcov = curve_fit(y,x,[P1,P[0],P[1],P[2]])
plt.plot(np.linspace(0,4,50),[y(popt[0],t) for t in np.linspace(0,4,50)],'r--')
plt.plot(x,[y(popt[0],t) for t in x],'b--')
plt.title('bit -')
print(popt[0])
return popt[0]
#黄金的交易额
def gold_trade(change): #w为累计涨跌幅
if(change < 0): #累积跌，则加仓
return abs(A_gold_down*np.exp(4*change/-0.037786983))
elif(change > 0): #累积涨，则减仓
return abs(A_gold_up*np.exp(4*change/0.035561898))
else:
return 0
#比特币交易额
def bit_trade(change): #w为累计涨跌幅
if(change < 0): #累积跌，则加仓
return abs(A_bit_down*np.exp(3*change/-0.125855917))
elif(change > 0): #累积涨，则减仓
return abs(A_bit_up*np.exp(4*change/0.177859096))
else:
return 0
第五步 按模型每天交易得出结果
注意：
- 每次交易会有佣金0.01，0.02。
- 判断今天是否是黄金的交易日
date_asset = {pd.to_datetime('2016-09-11'):[1000,0,0]} #字典存放所有天的资产组合情况[c,g,b]，第一天1000现金
# 存放的是黄金和比特币的份额
# 交易策略
def strategy(date,asset_date,b_price,g_price,bchange,gchange,workday): #price价格为今天的，pred预测为明天的，gold可选，若不传入则为0
asset_tomor = asset_date #asset_date是[]，现在的资产
if workday == 'False': #今天只能交易比特币
if bchange > 0: #减仓
bmin = min(asset_date[2]*b_price,bit_trade(bchange)) #卖出的金额
asset_tomor[0] = asset_date[0] + bmin*0.98
asset_tomor[2] = asset_date[2] - bmin/b_price #bit卖出的份额
elif bchange < 0: #加仓
bmin_add = min(asset_date[0],bit_trade(bchange)) #买入的金额
asset_tomor[0] = asset_date[0] - bmin_add
asset_tomor[2] = asset_date[2] + bmin_add*0.98/b_price #买入的份额
else: #平
pass
else:
if gchange > 0: #黄金减仓
gmin = min(asset_date[1]*g_price,gold_trade(gchange)) #卖出的金额
asset_tomor[0] = asset_date[0] + 0.99*gmin
asset_tomor[1] = asset_date[1] - gmin/g_price
if bchange > 0: #减仓
bmin = min(asset_date[2]*b_price,bit_trade(bchange)) #卖出的金额
asset_tomor[0] = asset_date[0] + bmin*0.98
asset_tomor[2] = asset_date[2] - bmin/b_price #bit卖出的份额
elif bchange < 0: #加仓
bmin_add = min(asset_date[0],bit_trade(bchange)) #买入的金额
asset_tomor[0] = asset_date[0] - bmin_add
asset_tomor[2] = asset_date[2] + bmin_add*0.98/b_price #买入的份额
else:
pass
elif gchange < 0 : #黄金加仓
gmin_add = min(asset_date[0],gold_trade(gchange)) #买多少
asset_tomor[0] = asset_date[0] - gmin_add
asset_tomor[1] = asset_date[1] + gmin_add*0.99/g_price
if bchange > 0: #减仓
bmin = min(asset_date[2]*b_price,bit_trade(bchange)) #卖出的金额
asset_tomor[0] = asset_date[0] + bmin*0.98
asset_tomor[2] = asset_date[2] - bmin/b_price #bit卖出的份额
elif bchange < 0: #加仓
bmin_add = min(asset_date[0],bit_trade(bchange)) #买入的金额
asset_tomor[0] = asset_date[0] - bmin_add
asset_tomor[2] = asset_date[2] + bmin_add*0.98/b_price #买入的份额
else:
pass
else: #黄金不变
if bchange > 0: #减仓
bmin = min(asset_date[2]*b_price,bit_trade(bchange)) #卖出的金额
asset_tomor[0] = asset_date[0] + bmin*0.98
asset_tomor[2] = asset_date[2] - bmin/b_price #bit卖出的份额
elif bchange < 0: #加仓
bmin_add = min(asset_date[0],bit_trade(bchange)) #买入的金额
asset_tomor[0] = asset_date[0] - bmin_add
asset_tomor[2] = asset_date[2] + bmin_add*0.98/b_price #买入的份额
else:
pass
return asset_tomor
for i in all_data.index:
asset_tomor = strategy(i,date_asset[i],all_data.bitcoin_value[i],all_data.gold_value[i],all_data.b_change[i],all_data.g_change[i],all_data.workday[i])
date_asset[i+dt.timedelta(1)] = asset_tomor.copy()
# 将每天的资产放入总数据中
asset_df = pd.DataFrame.from_dict(date_asset,orient='index',columns=['cash','gold','bitcoin'])
res = all_data.join(asset_df)
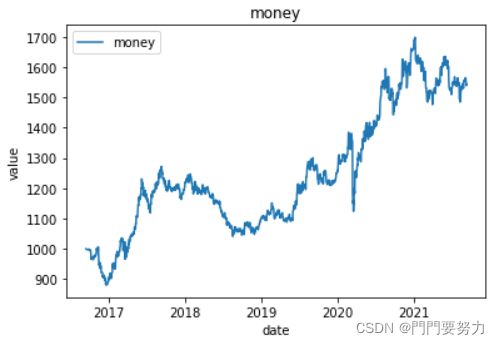
res['money'] = res.cash + res.gold*res.gold_value + res.bitcoin*res.bitcoin_value
# res.money.plot()
return res.money[-1] #返回最终持有资产的总额
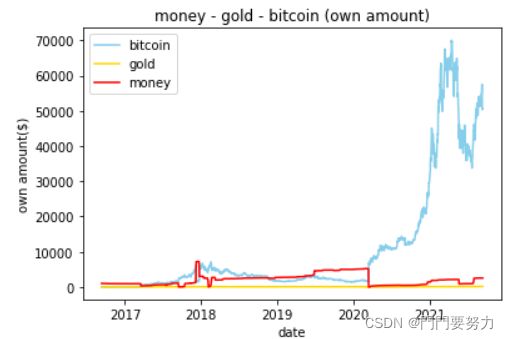
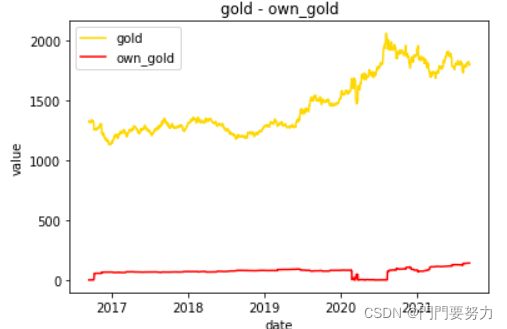
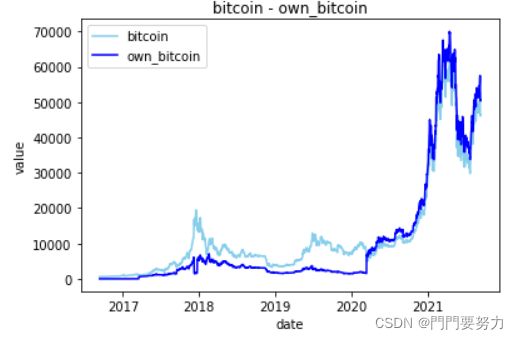
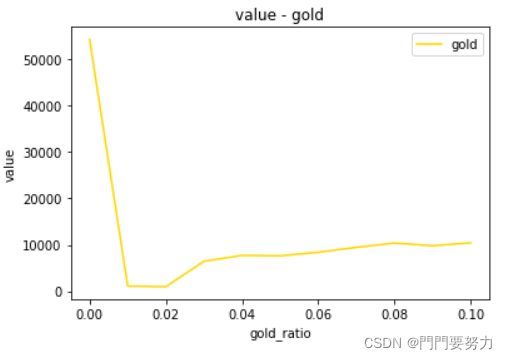
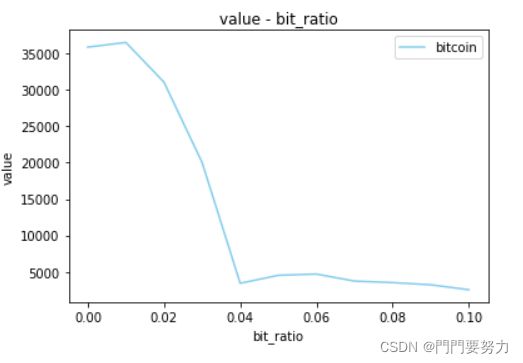
图
建模竞赛中，图是必不可少的且关键的输出。
该题中，我们需要
- 生成黄金、比特币的历史价格数据流图
- 预测的价格流与实际价格流的差异图
使用时间序列ARIMA模型学习，预测价格
- 产生ARIMA模型参数的图
一阶差分图判断d
BIC热力图
使用ACF与PACF判断p,q阶数
- 使用交易策略模型计算出的资金变动情况的图
现金+黄金+比特币的总价值变动
持有资产中现金-黄金-比特币的变动情况
黄金价格与所持黄金的价值变动趋势
比特币价格与所持比特币价值变动趋势
- 佣金对交易策略模型的影响
python的matplotlib库学习笔记
python的numpy库学习笔记
pandas库学习笔记