【ML】主成分分析 PCA（Principal Component Analysis）原理 + 实践 （基于sklearn）

原理简介

PCA（Principal Component Analysis）主成分分析，顾名思义，找出一组更低维度的特征，可以代表原始特征（精度会些许降低，但计算速度会大大加快）【主要目的是降维】。注意：不是筛选出原始维度的某几个维度，新的特征维度不是之前的特征维度，而是计算出来的新的特征数据。

详细推导可以参考这篇文章：https://www.jianshu.com/p/73080c9de848

实践

数据集

鸢尾花数据集：https://www.kaggle.com/datasets/himanshunakrani/iris-dataset

数据处理

import numpy as np
import pandas as pd

# 数据处理
origin_data = pd.read_csv("/kaggle/input/iris-dataset/iris.csv")
origin_data.loc[:,'species'].value_counts()
data = origin_data.replace({'species':{'setosa':1,'versicolor':2,'virginica':3}})

X = data.drop(columns=['species'])
y = data.loc[:,'species']

使用KNN模型进行分类预测（为了和PCA处理后做对比）

# 使用knn模型进行
from sklearn.neighbors import KNeighborsClassifier
# 周围3个点作为判断条件
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y)
y_predict = KNN.predict(X)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

输出：0.96

数据归一化

至于为什么要归一化：

1. 是为了加快计算速度
2. 因为需要距离计算，归一化后将各个维度量纲拍平

# 归一化
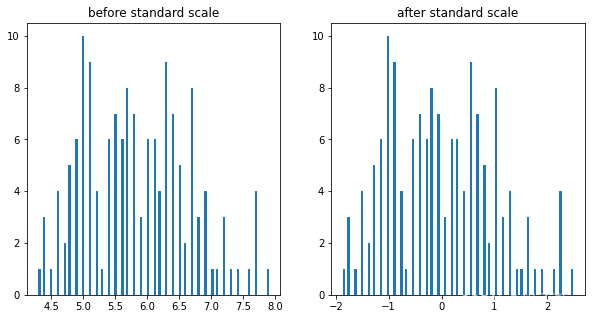
from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
print(type(X_norm)) # 

# 验证归一化后整体图形不变
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(10,5))
plt.subplot(121)
plt.hist(X.loc[:,'sepal_length'], bins=100)

plt.subplot(122)
plt.hist(X_norm[:,0], bins=100)
plt.show()

#归一化后 均值=0，标准差=1
print(X_norm[:,0].mean(), X_norm[:,0].std()) #-4.736951571734001e-16 1.0

归一化后，图像的形状不变

保持与原始数据维度数，观察维度方差占比

方差越小，说明数据变化越小，对结果的影响就越小

# 查看各个维度的方差
from sklearn.decomposition import PCA
# 四个维度都计算
pca = PCA(n_components=4)
x_pca = pca.fit_transform(X_norm)
print(pca.explained_variance_ratio_)

# 绘图更直观
fig2 = plt.figure(figsize=(10,5))
plt.bar([1,2,3,4],pca.explained_variance_ratio_)
# 注意已经不是原始的特征了，所以用PC1,2,3,4代替
plt.xticks([1,2,3,4],['PC1','PC2','PC3','PC4'])
plt.ylabel('pca variance ratio')
plt.show()

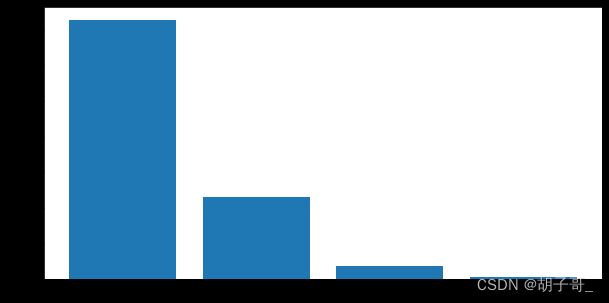
显然，有两个维度对结果影响很大，所以我们取两个维度作为特征维度。

计算两个维度的PCA

# 训练两个纬度的pca
pca_2 = PCA(n_components=2)
x_pca_2 = pca.fit_transform(X_norm)
print(type(x_pca_2))

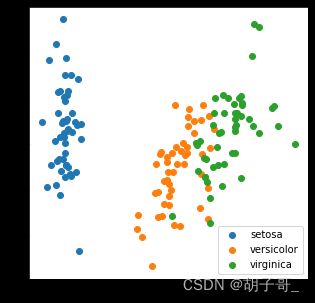
# 可视化两个维度
fig3 = plt.figure(figsize=(5,5))
setosa = plt.scatter(x_pca_2[:,0][y==1],x_pca_2[:,1][y==1])
versicolor = plt.scatter(x_pca_2[:,0][y==2],x_pca_2[:,1][y==2])
virginica = plt.scatter(x_pca_2[:,0][y==3],x_pca_2[:,1][y==3])
plt.legend((setosa,versicolor,virginica),('setosa','versicolor','virginica'))
plt.show()

再次用KNN计算PCA获取的新维度的准确度

# 再次训练，对比准确度变化
KNN_norm = KNeighborsClassifier(n_neighbors=3)
KNN_norm.fit(x_pca_2,y)
y_predict_norm = KNN_norm.predict(x_pca_2)
accuracy_norm = accuracy_score(y,y_predict_norm)
print(accuracy_norm)

输出：0.9533333333333334

总结

使用4个维度的准确率为：96%，使用PCA后的准确率是：95.3%，相差很小