周好蠢

Datawhale开源学习——数学建模之动态规划（上）

题目（由2020年国赛B题改编）：

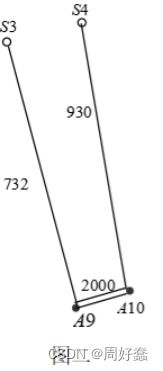
题目细节不过多赘述， $S_{i}$ 代表厂， $A_{i}$ 代表需要铺设的路，中间的数字代表里程数。

其中，运输及铺设每公里需要0.1万元。

本题计算最小值，故我认为不需要考虑铺设的成本，因为铺设的成本不含有变量，其值为常数，可在最后加上。

钢厂在指定期限内能生产该钢管的最大数量为个单位 , 钢管出厂销价 1 单位钢管为万元 , 如下表：
i	1	2	3	4	5	6	7
$S_{i}$	800	800	1000	2000	2000	2000	3000
$p_{i}$	160	155	155	160	155	150	160

解决此类规划问题的步骤：

1.把大问题分解为与原问题类似的子问题

2.确定优化的目标函数

3.决策变量个数的确定

4.约束关系的确定

5.再转化为大问题重复上述步骤

6.scipy求解

求解过程：

1.如下图即把大问题分解成一个子问题：

2.确定优化的目标函数 $f\left ( x \right )$

首先本题的成本即为采购和运输费用，分为设为 $C\left ( Buy \right )$ 、 $C\left ( Trans \right )$ ，

因此我们的目标函数即为 $min f\left ( x \right ) = min C\left ( Buy \right ) + min C \left ( Trans \right )$

3.决策变量的确定：

根据图二，我们可知有 $S_{3}$ 和 $S_{4}$ 两个厂，需要运输到 $A_{9}$ 和 $A_{10}$ 两个节点，

我们先假设 $S_{3}$ 提供 $x_{3}$ 的材料， $S_{4}$ 提供 $x_{4}$ 的材料，故

$f\left ( x \right ) = C\left ( Buy \right ) + C\left ( Trans \right ) = \left ( 155 x_{3} + 160x_{4} \right ) + \left ( 73.2+0.1 \right )x_{3}+\left ( 93+0.1 \right )x_{4} = 228.3x_{3}+253.1x_{4}$

4.约束关系的确定：

首先我们有两个变量 $x_{3}$ 、 $x_{4}$ ，我们需要对其做出约束，才能得出最优解。

$s.t. \left\{\begin{matrix} x_{3}+x{4}=2000 & \\ 0\leq x_{3}\leq 1000 & \\ 0\leq x_{4}\leq 2000 & \end{matrix}\right.$

5.转化到大问题来求解：

有了以上思路，对于我们大问题的求解提供了帮助，我们还需要解决以下问题：

解决思考题(以下内容摘自Gitmodel团队的运筹规划部分)：

该情形与上节的情形本质的不同便是我们需要考虑 $S_{3}$ 、 $S_{4}$ 对中间节点 $A_{10}$ 的运输计划， $S_{3}$ 、 $S_{4}$ 分别该往 $A_{10}$ 运输多少，运输后是往左边铺设还是右边铺设亦或两边一起铺设都是我们需要考虑的，因此对于三节点的情形，我们需要考虑第 i 个钢厂对中间节点 $A_{10}$ 运输钢管后从该节点出发，左边铺设的钢管量 $z_{i,10-}$ ，以及右边铺设的钢管量 $z_{i,10+}$ 。这里的正（负）号表示从节点 $A_{10}$ 的左边（右边）开始铺管。

而同样的,, 我们也可以引入 $S_{3}$ 运输至 $A_{9}$ 往右边铺设的钢管长度 $z_{3,9+}$ 以及 $S_{4}$ 运输至 $A_{11}$ 往左边铺设的钢管长度 $z_{4,11-}$ (思考一下: 为什么不考虑 $z_{3,11-}$ 、 $z_{4,9+}$ ) 从而替代掉整体的订购钢管长度 $x_{3}$ 、 $x_{4}$ 。

解：首先， $A_{9}$ 和 $A_{11}$ 为两个端点处，比较特殊，放大到原图也要考虑端点处，若需要考虑 $z_{3,11-}$ ，意味着我们 $S_{3}$ 的材料需要运送到 $A_{11}$ 开始逆向铺设，而逆向铺设需要两倍的运输费用，不如直接运输到 $A_{10}$ 边铺设边运输， $z_{4,9+}$ 同理可得。

我们构建上述关系。

6.使用scipy来计算：

根据上述思考题，我们可以不用考虑 $A_{1}$ 这个点，

本题为一个图论问题，先考虑各个厂到各个 $A_{i}$ 的最短路径，这样可以得到最少的运费。

因此我采用最短路算法，代码如下：

import math
 
nodes = ('A1','A2','A3','A4','A5','A6','A7','A8','A9','A10','A11'
         ,'A12','A13','A14','A15','A16','A17','A18','A19','A20','A21','A22','A23','A24',
        'A25','A26','A27','A28','A29','A30','A31','A32','A33','A34','A35','A36','A37','A38')
# dis矩阵为方阵
dis = [[0,3,450,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [3,0,math.inf,math.inf,301,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [450,math.inf,0,80,math.inf,1150,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,80,0,2,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,301,math.inf,2,0,math.inf,750,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,1150,math.inf,math.inf,0,600,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,1100,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,750,600,0,math.inf,606,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,0,10,306,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,606,10,0,math.inf,194,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,306,math.inf,0,5,195,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,194,5,0,math.inf,205,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,195,math.inf,0,10,math.inf,math.inf,20,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,205,10,0,math.inf,math.inf,31,201,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,0,1200,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,1100,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,1200,0,202,12,math.inf,720,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,20,31,202,0,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,201,12,math.inf,math.inf,0,math.inf,math.inf,680,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,0,690,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,720,math.inf,math.inf,690,0,42,520,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,680,math.inf,42,0,math.inf,480,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,520,math.inf,0,70,math.inf,170,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,480,70,0,math.inf,math.inf,math.inf,math.inf,300,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,0,690,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,170,math.inf,690,0,88,math.inf,math.inf,160,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,88,0,462,10,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,462,0,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,300,math.inf,math.inf,10,math.inf,0,math.inf,math.inf,220,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,160,math.inf,math.inf,math.inf,0,70,320,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,70,0,10,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,220,math.inf,10,0,math.inf,210,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,320,math.inf,math.inf,0,62,160,math.inf,math.inf,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,210,62,0,math.inf,math.inf,420,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,160,math.inf,0,70,30,290,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,70,0,110,math.inf,math.inf,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,420,30,110,0,math.inf,500,math.inf],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,290,math.inf,math.inf,0,20,30],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,500,20,0,20],
       [math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,math.inf,30,20,0]
      ]
 
def shortDistance(dis):
    for i in range(38):         # 十字交叉法的位置位置，先列后行
        for j in range(38):     # 列 表示dis[j][i]的值，即j->i
            for k in range(j+1, 38): # 行 表示dis[i][k]的值，即i->k，i只是一个桥梁而已
                # 先列后行，形成一个传递关系，若比原来距离小，则更新
                if dis[j][k] > dis[j][i] + dis[i][k]:
                    dis[j][k] = dis[j][i] + dis[i][k]
                    dis[k][j] = dis[j][i] + dis[i][k]

shortDistance(dis)

a = [16,14,18,23,26,34,38]
b = [2,5,7,9,11,13,17,20,22,27,30,32,35,37]
for i in a:
    print()
    for j in b:
        print(dis[i-1][j-1],end=' ')

dis1 = [
        [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
       [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
       [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
       [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
       [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
       [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
       [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
       [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
        [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
]

k = 0
l = 0
for i in a:
    k += 1
    for j in b:
        l = (l%14)+1
        dis1[k][l] = 0.1*dis[i-1][j-1]
        #print(k,l)

在通过scipy计算最小cost：

fun = lambda x :((160 * x[0] + 155*x[1] + 155*x[2]+ 160*x[3] +155*x[4] +150*x[5]+ 160*x[6]) 
    + 
        dis1[1][1] * (x[7]+x[8]) +  dis1[1][2] * (x[9]+x[10])+  dis1[1][3] * (x[11]+x[12])+  dis1[1][4] * (x[13]+x[14])+  dis1[1][5] * (x[15]+x[16])+  dis1[1][6] * (x[17]+x[18]) +  dis1[1][7] * (x[19]+x[20])+  
        dis1[1][8] * (x[21]+x[22])+  dis1[1][9] * (x[23]+x[24])+  dis1[1][10] * (x[25]+x[26])+  dis1[1][11] * (x[27]+x[28])+  dis1[1][12] * (x[29]+x[30])+  dis1[1][13] * (x[31]+x[32])+  dis1[1][14] * (x[33]+x[34])
    
    +   dis1[2][1] * (x[35]+x[36])+  dis1[2][2] * (x[37]+x[38])+  dis1[2][3] * (x[39]+x[40])+  dis1[2][4] * (x[41]+x[42])+  dis1[2][5] * (x[43]+x[44]) +  dis1[2][6] * (x[45]+x[46])+ dis1[2][7] * (x[47]+x[48])+
        dis1[2][8] * (x[49]+x[50])+  dis1[2][9] * (x[51]+x[52])+  dis1[2][10] * (x[53]+x[54])+  dis1[2][11] * (x[55]+x[56])+  dis1[2][12] * (x[57]+x[58])+  dis1[2][13] * (x[59]+x[60]) + dis1[2][14] * (x[61]+x[62])
   
    +   dis1[3][1] * (x[63]+x[64])+  dis1[3][2] * (x[65]+x[66])+  dis1[3][3] * (x[67]+x[68])+  dis1[3][4] * (x[69]+x[70])+  dis1[3][5] * (x[71]+x[72]) +  dis1[3][6] * (x[73]+x[74])+ dis1[3][7] * (x[75]+x[76])+
        dis1[3][8] * (x[77]+x[78])+  dis1[3][9] * (x[79]+x[80])+  dis1[3][10] * (x[81]+x[82])+  dis1[3][11] * (x[83]+x[84])+  dis1[3][12] * (x[85]+x[86])+  dis1[3][13] * (x[87]+x[88]) + dis1[3][14] * (x[89]+x[90])
    
    
    +   dis1[4][1] * (x[91]+x[92])+  dis1[4][2] * (x[93]+x[94])+  dis1[4][3] * (x[95]+x[96])+  dis1[4][4] * (x[97]+x[98])+  dis1[4][5] * (x[99]+x[100]) +  dis1[4][6] * (x[101]+x[102])+ dis1[4][7] * (x[103]+x[104])+
        dis1[4][8] * (x[105]+x[106])+  dis1[4][9] * (x[107]+x[108])+  dis1[4][10] * (x[109]+x[110])+  dis1[4][11] * (x[111]+x[112])+  dis1[4][12] * (x[113]+x[114])+  dis1[4][13] * (x[115]+x[116]) + dis1[4][14] * (x[117]+x[118])
        
    +   dis1[5][1] * (x[119]+x[120])+  dis1[5][2] * (x[121]+x[122])+  dis1[5][3] * (x[123]+x[124])+  dis1[5][4] * (x[125]+x[126])+  dis1[5][5] * (x[127]+x[128]) +  dis1[5][6] * (x[129]+x[130])+ dis1[5][7] * (x[131]+x[132])+
        dis1[5][8] * (x[133]+x[134])+  dis1[5][9] * (x[135]+x[136])+  dis1[5][10] * (x[137]+x[138])+  dis1[5][11] * (x[139]+x[140])+  dis1[5][12] * (x[141]+x[142])+  dis1[5][13] * (x[143]+x[144]) + dis1[5][14] * (x[145]+x[146])
        
    +   dis1[6][1] * (x[147]+x[148])+  dis1[6][2] * (x[149]+x[150])+  dis1[6][3] * (x[151]+x[152])+  dis1[6][4] * (x[153]+x[154])+  dis1[6][5] * (x[155]+x[156]) +  dis1[6][6] * (x[157]+x[158])+ dis1[6][7] * (x[159]+x[160])+
        dis1[6][8] * (x[161]+x[162])+  dis1[6][9] * (x[163]+x[164])+  dis1[6][10] * (x[165]+x[166])+  dis1[6][11] * (x[167]+x[168])+  dis1[6][12] * (x[169]+x[170])+  dis1[6][13] * (x[171]+x[172]) + dis1[6][14] * (x[173]+x[174])
        
    +   dis1[7][1] * (x[175]+x[176])+  dis1[7][2] * (x[177]+x[178])+  dis1[7][3] * (x[179]+x[180])+  dis1[7][4] * (x[181]+x[182])+  dis1[7][5] * (x[183]+x[184]) +  dis1[7][6] * (x[185]+x[186])+ dis1[7][7] * (x[187]+x[188])+
        dis1[7][8] * (x[189]+x[190])+  dis1[7][9] * (x[191]+x[192])+  dis1[7][10] * (x[193]+x[194])+  dis1[7][11] * (x[195]+x[196])+  dis1[7][12] * (x[197]+x[198])+  dis1[7][13] * (x[199]+x[200]) + dis1[7][14] * (x[201]+x[202])
        )
cons = ({'type': 'eq', 'fun': lambda x: x[0] - x[7] - x[8] - x[9]- x[10]- x[11] - x[12] - x[13]- x[14]- x[15] - x[16] - x[17]- x[18]- x[19] - x[20] - x[21]- x[22]- x[23] - x[24] - x[25]- x[26]- x[27] - x[28] - x[29]- x[30]- x[31] - x[32] - x[33]- x[34]}, # 等式约束
        {'type': 'eq', 'fun': lambda x: x[1] - x[35] - x[36] - x[37]- x[38]- x[39] - x[40] - x[41]- x[42]- x[43] - x[44] - x[45]- x[46]- x[47] - x[48] - x[49]- x[50]- x[51] - x[52] - x[53]- x[54]- x[55] - x[56] - x[57]- x[58]- x[59] - x[60] - x[61]- x[62]},
        {'type': 'eq', 'fun': lambda x: x[2] - x[63] - x[64] - x[65]- x[66]- x[67] - x[68] - x[69]- x[70]- x[71] - x[72] - x[73]- x[74]- x[75] - x[76] - x[77]- x[78]- x[79] - x[80] - x[81]- x[82]- x[83] - x[84] - x[85]- x[86]- x[87] - x[88] - x[89]- x[90]},
        {'type': 'eq', 'fun': lambda x: x[3] - x[91] - x[92] - x[93]- x[94]- x[95] - x[96] - x[97]- x[98]- x[99] - x[100] - x[101]- x[102]- x[103] - x[104] - x[105]- x[106]- x[107] - x[108] - x[109]- x[110]- x[111] - x[112] - x[113]- x[114]- x[115] - x[116] - x[117]- x[118]},
        {'type': 'eq', 'fun': lambda x: x[4] - x[119] - x[120] - x[121]- x[122]- x[123] - x[124] - x[125]- x[126]- x[127] - x[128] - x[129]- x[130]- x[131] - x[132] - x[133]- x[134]- x[135] - x[136] - x[137]- x[138]- x[139] - x[140] - x[141]- x[142]- x[143] - x[144] - x[145]- x[146]},
        {'type': 'eq', 'fun': lambda x: x[5] - x[147] - x[148] - x[149]- x[150]- x[151] - x[152] - x[153]- x[154]- x[155] - x[156] - x[157]- x[158]- x[159] - x[160] - x[161]- x[162]- x[163] - x[164] - x[165]- x[166]- x[167] - x[168] - x[169]- x[170]- x[171] - x[172] - x[173]- x[174]},
        {'type': 'eq', 'fun': lambda x: x[6] - x[175] - x[176] - x[177]- x[178]- x[179] - x[180] - x[181]- x[182]- x[183] - x[184] - x[185]- x[186]- x[187] - x[188] - x[189]- x[190]- x[191] - x[192] - x[193]- x[194]- x[195] - x[196] - x[197]- x[198]- x[199] - x[200] - x[201]- x[202]},
        
        
        {'type': 'ineq', 'fun': lambda x: 800 - x[0]}, # 不等式约束
        {'type': 'ineq', 'fun': lambda x: 800 - x[1]}, # 不等式约束
        {'type': 'ineq', 'fun': lambda x: 1000 - x[2]}, # 不等式约束
        {'type': 'ineq', 'fun': lambda x: 2000 - x[3]}, # 不等式约束
        {'type': 'ineq', 'fun': lambda x: 2000 - x[4]}, # 不等式约束
        {'type': 'ineq', 'fun': lambda x: 2000 - x[5]}, # 不等式约束
        {'type': 'ineq', 'fun': lambda x: 3000 - x[6]}, # 不等式约束
        
        
        
        {'type': 'eq', 'fun': lambda x: x[0] + x[1]+ x[2]+ x[3]+ x[4]+ x[5]+ x[6] - 5171},
 
        {'type': 'ineq', 'fun': lambda x: x[7]},
        {'type': 'ineq', 'fun': lambda x: x[8]},
        {'type': 'ineq', 'fun': lambda x: x[9]},
        {'type': 'ineq', 'fun': lambda x: x[10]},
        {'type': 'ineq', 'fun': lambda x: x[11]},
        {'type': 'ineq', 'fun': lambda x: x[12]},
        {'type': 'ineq', 'fun': lambda x: x[13]},
        {'type': 'ineq', 'fun': lambda x: x[14]},
        {'type': 'ineq', 'fun': lambda x: x[15]},
        {'type': 'ineq', 'fun': lambda x: x[16]},
        {'type': 'ineq', 'fun': lambda x: x[17]},
        {'type': 'ineq', 'fun': lambda x: x[18]},
        {'type': 'ineq', 'fun': lambda x: x[19]},
        {'type': 'ineq', 'fun': lambda x: x[20]},
        {'type': 'ineq', 'fun': lambda x: x[21]},
        {'type': 'ineq', 'fun': lambda x: x[22]},
        {'type': 'ineq', 'fun': lambda x: x[23]},
        {'type': 'ineq', 'fun': lambda x: x[24]},
        {'type': 'ineq', 'fun': lambda x: x[25]},
        {'type': 'ineq', 'fun': lambda x: x[26]},
        {'type': 'ineq', 'fun': lambda x: x[27]},
        {'type': 'ineq', 'fun': lambda x: x[28]},
        {'type': 'ineq', 'fun': lambda x: x[29]},
        {'type': 'ineq', 'fun': lambda x: x[30]},
        {'type': 'ineq', 'fun': lambda x: x[31]},
        {'type': 'ineq', 'fun': lambda x: x[32]},
        {'type': 'ineq', 'fun': lambda x: x[33]},
        {'type': 'ineq', 'fun': lambda x: x[34]},
        
        {'type': 'ineq', 'fun': lambda x: x[35]},
        {'type': 'ineq', 'fun': lambda x: x[36]},
        {'type': 'ineq', 'fun': lambda x: x[37]},
        {'type': 'ineq', 'fun': lambda x: x[38]},
        {'type': 'ineq', 'fun': lambda x: x[39]},
        {'type': 'ineq', 'fun': lambda x: x[40]},
        {'type': 'ineq', 'fun': lambda x: x[41]},
        {'type': 'ineq', 'fun': lambda x: x[42]},
        {'type': 'ineq', 'fun': lambda x: x[43]},
        {'type': 'ineq', 'fun': lambda x: x[44]},
        {'type': 'ineq', 'fun': lambda x: x[45]},
        {'type': 'ineq', 'fun': lambda x: x[46]},
        {'type': 'ineq', 'fun': lambda x: x[47]},
        {'type': 'ineq', 'fun': lambda x: x[48]},
        {'type': 'ineq', 'fun': lambda x: x[49]},
        {'type': 'ineq', 'fun': lambda x: x[50]},
        {'type': 'ineq', 'fun': lambda x: x[51]},
        {'type': 'ineq', 'fun': lambda x: x[52]},
        {'type': 'ineq', 'fun': lambda x: x[53]},
        {'type': 'ineq', 'fun': lambda x: x[54]},
        {'type': 'ineq', 'fun': lambda x: x[55]},
        {'type': 'ineq', 'fun': lambda x: x[56]},
        {'type': 'ineq', 'fun': lambda x: x[57]},
        {'type': 'ineq', 'fun': lambda x: x[58]},
        {'type': 'ineq', 'fun': lambda x: x[59]},
        {'type': 'ineq', 'fun': lambda x: x[60]},
        {'type': 'ineq', 'fun': lambda x: x[61]},
        {'type': 'ineq', 'fun': lambda x: x[62]},
        
        {'type': 'ineq', 'fun': lambda x: x[63]},
        {'type': 'ineq', 'fun': lambda x: x[64]},
        {'type': 'ineq', 'fun': lambda x: x[65]},
        {'type': 'ineq', 'fun': lambda x: x[66]},
        {'type': 'ineq', 'fun': lambda x: x[67]},
        {'type': 'ineq', 'fun': lambda x: x[68]},
        {'type': 'ineq', 'fun': lambda x: x[69]},
        {'type': 'ineq', 'fun': lambda x: x[70]},
        {'type': 'ineq', 'fun': lambda x: x[71]},
        {'type': 'ineq', 'fun': lambda x: x[72]},
        {'type': 'ineq', 'fun': lambda x: x[73]},
        {'type': 'ineq', 'fun': lambda x: x[74]},
        {'type': 'ineq', 'fun': lambda x: x[75]},
        {'type': 'ineq', 'fun': lambda x: x[76]},
        {'type': 'ineq', 'fun': lambda x: x[77]},
        {'type': 'ineq', 'fun': lambda x: x[78]},
        {'type': 'ineq', 'fun': lambda x: x[79]},
        {'type': 'ineq', 'fun': lambda x: x[80]},
        {'type': 'ineq', 'fun': lambda x: x[81]},
        {'type': 'ineq', 'fun': lambda x: x[82]},
        {'type': 'ineq', 'fun': lambda x: x[83]},
        {'type': 'ineq', 'fun': lambda x: x[84]},
        {'type': 'ineq', 'fun': lambda x: x[85]},
        {'type': 'ineq', 'fun': lambda x: x[86]},
        {'type': 'ineq', 'fun': lambda x: x[87]},
        {'type': 'ineq', 'fun': lambda x: x[88]},
        {'type': 'ineq', 'fun': lambda x: x[89]},
        {'type': 'ineq', 'fun': lambda x: x[90]},
        
        {'type': 'ineq', 'fun': lambda x: x[91]},
        {'type': 'ineq', 'fun': lambda x: x[92]},
        {'type': 'ineq', 'fun': lambda x: x[93]},
        {'type': 'ineq', 'fun': lambda x: x[94]},
        {'type': 'ineq', 'fun': lambda x: x[95]},
        {'type': 'ineq', 'fun': lambda x: x[96]},
        {'type': 'ineq', 'fun': lambda x: x[97]},
        {'type': 'ineq', 'fun': lambda x: x[98]},
        {'type': 'ineq', 'fun': lambda x: x[99]},
        {'type': 'ineq', 'fun': lambda x: x[100]},
        {'type': 'ineq', 'fun': lambda x: x[101]},
        {'type': 'ineq', 'fun': lambda x: x[102]},
        {'type': 'ineq', 'fun': lambda x: x[103]},
        {'type': 'ineq', 'fun': lambda x: x[104]},
        {'type': 'ineq', 'fun': lambda x: x[105]},
        {'type': 'ineq', 'fun': lambda x: x[106]},
        {'type': 'ineq', 'fun': lambda x: x[107]},
        {'type': 'ineq', 'fun': lambda x: x[108]},
        {'type': 'ineq', 'fun': lambda x: x[109]},
        {'type': 'ineq', 'fun': lambda x: x[110]},
        {'type': 'ineq', 'fun': lambda x: x[111]},
        {'type': 'ineq', 'fun': lambda x: x[112]},
        {'type': 'ineq', 'fun': lambda x: x[113]},
        {'type': 'ineq', 'fun': lambda x: x[114]},
        {'type': 'ineq', 'fun': lambda x: x[115]},
        {'type': 'ineq', 'fun': lambda x: x[116]},
        {'type': 'ineq', 'fun': lambda x: x[117]},
        {'type': 'ineq', 'fun': lambda x: x[118]},
        
        {'type': 'ineq', 'fun': lambda x: x[119]},
        {'type': 'ineq', 'fun': lambda x: x[120]},
        {'type': 'ineq', 'fun': lambda x: x[121]},
        {'type': 'ineq', 'fun': lambda x: x[122]},
        {'type': 'ineq', 'fun': lambda x: x[123]},
        {'type': 'ineq', 'fun': lambda x: x[124]},
        {'type': 'ineq', 'fun': lambda x: x[125]},
        {'type': 'ineq', 'fun': lambda x: x[126]},
        {'type': 'ineq', 'fun': lambda x: x[127]},
        {'type': 'ineq', 'fun': lambda x: x[128]},
        {'type': 'ineq', 'fun': lambda x: x[129]},
        {'type': 'ineq', 'fun': lambda x: x[130]},
        {'type': 'ineq', 'fun': lambda x: x[131]},
        {'type': 'ineq', 'fun': lambda x: x[132]},
        {'type': 'ineq', 'fun': lambda x: x[133]},
        {'type': 'ineq', 'fun': lambda x: x[134]},
        {'type': 'ineq', 'fun': lambda x: x[135]},
        {'type': 'ineq', 'fun': lambda x: x[136]},
        {'type': 'ineq', 'fun': lambda x: x[137]},
        {'type': 'ineq', 'fun': lambda x: x[138]},
        {'type': 'ineq', 'fun': lambda x: x[139]},
        {'type': 'ineq', 'fun': lambda x: x[140]},
        {'type': 'ineq', 'fun': lambda x: x[141]},
        {'type': 'ineq', 'fun': lambda x: x[142]},
        {'type': 'ineq', 'fun': lambda x: x[143]},
        {'type': 'ineq', 'fun': lambda x: x[144]},
        {'type': 'ineq', 'fun': lambda x: x[145]},
        {'type': 'ineq', 'fun': lambda x: x[146]},
        
        
        {'type': 'ineq', 'fun': lambda x: x[147]},
        {'type': 'ineq', 'fun': lambda x: x[148]},
        {'type': 'ineq', 'fun': lambda x: x[149]},
        {'type': 'ineq', 'fun': lambda x: x[150]},
        {'type': 'ineq', 'fun': lambda x: x[151]},
        {'type': 'ineq', 'fun': lambda x: x[152]},
        {'type': 'ineq', 'fun': lambda x: x[153]},
        {'type': 'ineq', 'fun': lambda x: x[154]},
        {'type': 'ineq', 'fun': lambda x: x[155]},
        {'type': 'ineq', 'fun': lambda x: x[156]},
        {'type': 'ineq', 'fun': lambda x: x[157]},
        {'type': 'ineq', 'fun': lambda x: x[158]},
        {'type': 'ineq', 'fun': lambda x: x[159]},
        {'type': 'ineq', 'fun': lambda x: x[160]},
        {'type': 'ineq', 'fun': lambda x: x[161]},
        {'type': 'ineq', 'fun': lambda x: x[162]},
        {'type': 'ineq', 'fun': lambda x: x[163]},
        {'type': 'ineq', 'fun': lambda x: x[164]},
        {'type': 'ineq', 'fun': lambda x: x[165]},
        {'type': 'ineq', 'fun': lambda x: x[166]},
        {'type': 'ineq', 'fun': lambda x: x[167]},
        {'type': 'ineq', 'fun': lambda x: x[168]},
        {'type': 'ineq', 'fun': lambda x: x[169]},
        {'type': 'ineq', 'fun': lambda x: x[170]},
        {'type': 'ineq', 'fun': lambda x: x[171]},
        {'type': 'ineq', 'fun': lambda x: x[172]},
        {'type': 'ineq', 'fun': lambda x: x[173]},
        {'type': 'ineq', 'fun': lambda x: x[174]},
        
        {'type': 'ineq', 'fun': lambda x: x[175]},
        {'type': 'ineq', 'fun': lambda x: x[176]},
        {'type': 'ineq', 'fun': lambda x: x[177]},
        {'type': 'ineq', 'fun': lambda x: x[178]},
        {'type': 'ineq', 'fun': lambda x: x[179]},
        {'type': 'ineq', 'fun': lambda x: x[180]},
        {'type': 'ineq', 'fun': lambda x: x[181]},
        {'type': 'ineq', 'fun': lambda x: x[182]},
        {'type': 'ineq', 'fun': lambda x: x[183]},
        {'type': 'ineq', 'fun': lambda x: x[184]},
        {'type': 'ineq', 'fun': lambda x: x[185]},
        {'type': 'ineq', 'fun': lambda x: x[186]},
        {'type': 'ineq', 'fun': lambda x: x[187]},
        {'type': 'ineq', 'fun': lambda x: x[188]},
        {'type': 'ineq', 'fun': lambda x: x[189]},
        {'type': 'ineq', 'fun': lambda x: x[190]},
        {'type': 'ineq', 'fun': lambda x: x[191]},
        {'type': 'ineq', 'fun': lambda x: x[192]},
        {'type': 'ineq', 'fun': lambda x: x[193]},
        {'type': 'ineq', 'fun': lambda x: x[194]},
        {'type': 'ineq', 'fun': lambda x: x[195]},
        {'type': 'ineq', 'fun': lambda x: x[196]},
        {'type': 'ineq', 'fun': lambda x: x[197]},
        {'type': 'ineq', 'fun': lambda x: x[198]},
        {'type': 'ineq', 'fun': lambda x: x[199]},
        {'type': 'ineq', 'fun': lambda x: x[200]},
        {'type': 'ineq', 'fun': lambda x: x[201]},
        {'type': 'ineq', 'fun': lambda x: x[202]}
        
       )

x0 = np.ones(203) # 设置初始值(随机设置即可)

res = minimize(fun, x0, method='SLSQP', constraints=cons) # 调用最小值模块
res

最后计算Cost约为833579.1万元。（计算结果）

使用ortools计算：

from ortools.linear_solver import pywraplp
import math
solver = pywraplp.Solver.CreateSolver('GLOP')
x3 = solver.NumVar(0, 1000, 'x3') 
x4 = solver.NumVar(0, 1600, 'x4')
x5 = solver.NumVar(0,math.inf,'x5')
x6 = solver.NumVar(0,math.inf,'x6')
x7 = solver.NumVar(0,math.inf,'x7')
x8 = solver.NumVar(0,math.inf,'x8')
x9 = solver.NumVar(0,math.inf,'x9')
x10 = solver.NumVar(0,math.inf,'x10')

print('变量个数 =', solver.NumVariables())


solver.Add(x3 + x4 == 780)
solver.Add(x3 == x5+x6+x7)
solver.Add(x4 == x8+x9+x10)
print('约束个数 =', solver.NumConstraints())

solver.Minimize(155 * x3 + 160 * x4 + 73.3 * x5 + 101.1 * (x6 + x7) + 93.1 * (x8 + x9) + 78.9 * x10)
status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print('最优值 =', solver.Objective().Value())
    print('x3', x3.solution_value())
    print('x4', x4.solution_value())
    print('x5', x5.solution_value())
    print('x6', x6.solution_value())
    print('x7', x7.solution_value())
    print('x8', x8.solution_value())
    print('x9', x9.solution_value())
    print('x10', x10.solution_value())

else:
    print('The problem does not have an optimal solution.')

计算结果与传统算法一致：

本次学习心得，使用ortools计算比较方便，传统的约束格式比较复杂，不易于记忆，两个作业题均已完成，解答过程可能有错误，希望大家批评指正！

你可能感兴趣的:(笔记,建模,数学,开源,学习,java)

情绪觉察日记第37天露露_e800
今天是家庭关系规划师的第二阶最后一天，慧萍老师帮我做了个案，帮我处理了埋在心底好多年的一份恐惧，并给了我深深的力量！这几天出来学习，爸妈过来婆家帮我带小孩，妈妈出于爱帮我收拾东西，并跟我先生和婆婆产生矛盾，妈妈觉得他们没有照顾好我…。今晚回家见到妈妈，我很欣赏她并赞扬她，妈妈说今晚要跟我睡我说好，当我们俩躺在床上准备睡觉的时候，我握着妈妈的手对她说:妈妈这几天辛苦你了，你看你多利害把我们的家收拾得
机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
铭刻于星（四十二）随风至
69夜晚，绍敏同学做完功课后，看了眼房外，没听到动静才敢从书包的夹层里拿出那个心形纸团。折痕压得很深，都有些旧了，想来是已经写好很久了。绍敏同学慢慢地、轻轻地捏开折叠处，待到全部拆开后，又反复抚平纸张，然后仔细地一字字默看。只是开头的三个字是第一次看到，让她心漏跳了几拍。“亲爱的绍敏：从四年级的时候，我就喜欢你了，但是我一直不敢说，怕影响你学习。六年级的时候听说有人跟你表白，你接受了，我很难过，但
UI学习——cell的复用和自定义cell Magnetic_h ui 学习
目录cell的复用手动（非注册）自动（注册）自定义cellcell的复用在iOS开发中，单元格复用是一种提高表格（UITableView）和集合视图（UICollectionView）滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时，如果没有可复用的单元格，则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕，它就不会被销毁。相反，它被添
10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
学点心理知识，呵护孩子健康静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
《投行人生》读书笔记小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
Long类型前后端数据不一致 igotyback 前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
LocalDateTime 转 String igotyback java 开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类 qt 开发语言 sdl2 linux
需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
ArcGIS栅格计算器常见公式（赋值、0和空值的转换、补充栅格空值）研学随笔 arcgis 经验分享
我们在使用ArcGIS时通常经常用到栅格计算器，今天主要给大家介绍我日常中经常用到的几个公式，供大家参考学习。将特定值（-9999）赋值为0，例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值（如0）Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值，其他保留原值SetNull("raster"==
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录 leetcode 算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
git常用命令笔记咩酱-小羊 git 笔记
###用习惯了idea总是不记得git的一些常见命令，需要用到的时候总是担心旁边站了人~~~记个笔记@_@，告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"[email protected]"基本操作克隆远程仓库gitclone查看
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
2019-12-22-22:30 涓涓1016
今天是冬至，写下我的日更，是因为这两天的学习真的是能量的满满，让我看到了自己，未来另外一种可能性，也让我看到了这两年这几年的过程中我所接受那些痛苦的来源。一切的根源和痛苦都来自于人生，家庭，而你的原生家庭，你的爸爸和妈妈，是因为你这个灵魂在那一刻选择他们作为你的爸爸和妈妈来的，所以你得接受他，你得接纳他，他就是因为他的存在而给你的学习和成长带来这些痛苦，那其实是你必然要经历的这个过程，当你去接纳的
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
509. 斐波那契数(每日一题) lzyprime
lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
拥有断舍离的心态，过精简生活--《断舍离》读书笔记爱吃丸子的小樱桃
不知不觉间房间里的东西越来越多，虽然摆放整齐，但也时常会觉得空间逼仄，令人心生烦闷。抱着断舍离的态度，我开始阅读《断舍离》这本书，希望从书中能找到一些有效的方法，帮助我实现空间、物品上的断舍离。《断舍离》是日本作家山下英子通过自己的经历、思考和实践总结而成的，整体内涵也从刚开始的私人生活哲学的“断舍离”升华成了“人生实践哲学”，接着又成为每个人都能实行的“改变人生的断舍离”，从“哲学”逐渐升华成“
四章-32-点要素的聚合彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记，使用的openlayers5.3.xapi。源码见1032.html，对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
DIV+CSS+JavaScript技术制作网页（旅游主题网页设计与制作）云南大理 STU学生网页设计网页设计期末网页作业 html静态网页 html5期末大作业网页设计 web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业：【HTML5网页期末作业(1000套)】程序员有趣的告白方式：【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面：计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
【华为OD机试真题2023B卷 JAVA&JS】We Are A Team 若博豆 java 算法华为 javascript
华为OD2023（B卷）机试题库全覆盖，刷题指南点这里WeAreATeam时间限制：1秒|内存限制：32768K|语言限制：不限题目描述：总共有n个人在机房，每个人有一个标号（1<=标号<=n），他们分成了多个团队，需要你根据收到的m条消息判定指定的两个人是否在一个团队中，具体的：1、消息构成为：abc，整数a、b分别代
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
398顺境，逆境戴骁勇
2018.11.27周二雾霾最近儿子进入了一段顺境期，今天表现尤其不错。今天的数学测试成绩喜人，没有出现以往的计算错误，整个卷面书写工整，附加题也在规定时间内完成且做对。为迎接体育测试的锻炼有了质的飞跃。坐位体前屈成绩突飞猛进，估测成绩能达到12cm，这和上次测试的零分来比，简直是逆袭。儿子还在不断锻炼和提升，唯恐到时候掉链子。跑步姿势在我的调教下，逐渐正规起来，速度随之也有了提升。今晚测试的50
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
在一台Ubuntu计算机上构建Hyperledger Fabric网络落叶无声9 区块链超级账本 Hyperledger fabric 区块链 ubuntu 构建 hyperledger fabric
在一台Ubuntu计算机上构建HyperledgerFabric网络Hyperledgerfabric是一个开源的区块链应用程序平台，为开发基于区块链的应用程序提供了一个起点。当我们提到HyperledgerFabric网络时，我们指的是使用HyperledgerFabric的正在运行的系统。即使只使用最少数量的组件，部署Fabric网络也不是一件容易的事。Fabric社区创建了一个名为Cello
GitHub上克隆项目 bigbig猩猩 github
从GitHub上克隆项目是一个简单且直接的过程，它允许你将远程仓库中的项目复制到你的本地计算机上，以便进行进一步的开发、测试或学习。以下是一个详细的步骤指南，帮助你从GitHub上克隆项目。一、准备工作1.安装Git在克隆GitHub项目之前，你需要在你的计算机上安装Git工具。Git是一个开源的分布式版本控制系统，用于跟踪和管理代码变更。你可以从Git的官方网站（https://git-scm.
关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript 二挡起步 web前端期末大作业 javascript html css 旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业，Web大学生网页HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
HTML网页设计制作大作业（div+css）云南我的家乡旅游景点带文字滚动二挡起步 web前端期末大作业 web设计网页规划与设计 html css javascript dreamweaver 前端
Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript：做与用户的交互行为文章目录前端学习路线
js动画html标签（持续更新中） 843977358 html js 动画 media opacity
1.jQuery 效果 - animate() 方法改变 "div" 元素的高度： $(".btn1").click(function(){ $("#box").animate({height:"300px
springMVC学习笔记 caoyong springMVC
1、搭建开发环境 a>、添加jar文件，在ioc所需jar包的基础上添加spring-web.jar,spring-webmvc.jar b>、在web.xml中配置前端控制器 <servlet> &nbs
POI中设置Excel单元格格式 107x poi style 列宽合并单元格自动换行
引用：http://apps.hi.baidu.com/share/detail/17249059 POI中可能会用到一些需要设置EXCEL单元格格式的操作小结：先获取工作薄对象: HSSFWorkbook wb = new HSSFWorkbook(); HSSFSheet sheet = wb.createSheet(); HSSFCellStyle setBorder = wb.
jquery 获取A href 触发js方法的this参数无效的情况一炮送你回车库 jquery
html如下： <td class=\"bord-r-n bord-l-n c-333\"> <a class=\"table-icon edit\" onclick=\"editTrValues(this);\">修改</a> </td>" j
md5 3213213333332132 MD5
import java.security.MessageDigest; import java.security.NoSuchAlgorithmException; public class MDFive { public static void main(String[] args) { String md5Str = "cq
完全卸载干净Oracle11g sophia天雪 orale数据库卸载干净清理注册表
完全卸载干净Oracle11g A、存在OUI卸载工具的情况下：第一步：停用所有Oracle相关的已启动的服务；第二步：找到OUI卸载工具：在“开始”菜单中找到“oracle_OraDb11g_home”文件夹中 &
apache 的access.log 日志文件太大如何解决 darkranger apache
CustomLog logs/access.log common 此写法导致日志数据一致自增变大。直接注释上面的语法 #CustomLog logs/access.log common 增加： CustomLog "|bin/rotatelogs.exe -l logs/access-%Y-%m-d.log
Hadoop单机模式环境搭建关键步骤 aijuans 分布式
Hadoop环境需要sshd服务一直开启，故，在服务器上需要按照ssh服务，以Ubuntu Linux为例，按照ssh服务如下： sudo apt-get install ssh sudo apt-get install rsync 编辑HADOOP_HOME/conf/hadoop-env.sh文件，将JAVA_HOME设置为Java
PL/SQL DEVELOPER 使用的一些技巧 atongyeye java sql
1 记住密码这是个有争议的功能，因为记住密码会给带来数据安全的问题。但假如是开发用的库，密码甚至可以和用户名相同，每次输入密码实在没什么意义，可以考虑让PLSQL Developer记住密码。位置：Tools菜单－－Preferences－－Oracle－－Logon HIstory－－Store with password 2 特殊Copy 在SQL Window
PHP：在对象上动态添加一个新的方法 bardo 方法动态添加闭包
有关在一个对象上动态添加方法，如果你来自Ruby语言或您熟悉这门语言，你已经知道它是什么...... Ruby提供给你一种方式来获得一个instancied对象，并给这个对象添加一个额外的方法。好！不说Ruby了，让我们来谈谈PHP PHP未提供一个“标准的方式”做这样的事情，这也是没有核心的一部分... 但无论如何，它并没有说我们不能做这样
ThreadLocal与线程安全 bijian1013 java java多线程 threadLocal
首先来看一下线程安全问题产生的两个前提条件： 1.数据共享，多个线程访问同样的数据。 2.共享数据是可变的，多个线程对访问的共享数据作出了修改。实例：定义一个共享数据： public static int a = 0;
Tomcat 架包冲突解决征客丶 tomcat Web
环境： Tomcat 7.0.6 win7 x64 错误表象：【我的冲突的架包是：catalina.jar 与 tomcat-catalina-7.0.61.jar 冲突，不知道其他架包冲突时是不是也报这个错误】严重: End event threw exception java.lang.NoSuchMethodException: org.apache.catalina.dep
【Scala三】分析Spark源代码总结的Scala语法一 bit1129 scala
Scala语法 1. classOf运算符 Scala中的classOf[T]是一个class对象，等价于Java的T.class,比如classOf[TextInputFormat]等价于TextInputFormat.class 2. 方法默认值 defaultMinPartitions就是一个默认值，类似C++的方法默认值
java 线程池管理机制 BlueSkator java线程池管理机制
编辑 Add Tools jdk线程池一、引言第一：降低资源消耗。通过重复利用已创建的线程降低线程创建和销毁造成的消耗。第二：提高响应速度。当任务到达时，任务可以不需要等到线程创建就能立即执行。第三：提高线程的可管理性。线程是稀缺资源，如果无限制的创建，不仅会消耗系统资源，还会降低系统的稳定性，使用线程池可以进行统一的分配，调优和监控。
关于hql中使用本地sql函数的问题（问-答） BreakingBad HQL 存储函数
转自于：http://www.iteye.com/problems/23775 问：我在开发过程中，使用hql进行查询（mysql5）使用到了mysql自带的函数find_in_set()这个函数作为匹配字符串的来讲效率非常好，但是我直接把它写在hql语句里面（from ForumMemberInfo fm,ForumArea fa where find_in_set(fm.userId,f
读《研磨设计模式》-代码笔记-迭代器模式-Iterator bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ import java.util.Arrays; import java.util.List; /** * Iterator模式提供一种方法顺序访问一个聚合对象中各个元素，而又不暴露该对象内部表示 * * 个人觉得，为了不暴露该
常用SQL chenjunt3 oracle sql C++c C#
--NC建库 CREATE TABLESPACE NNC_DATA01 DATAFILE 'E:\oracle\product\10.2.0\oradata\orcl\nnc_data01.dbf' SIZE 500M AUTOEXTEND ON NEXT 50M EXTENT MANAGEMENT LOCAL UNIFORM SIZE 256K ; CREATE TABLESPA
数学是科学技术的语言 comsci 工作活动领域模型
从小学到大学都在学习数学，从小学开始了解数字的概念和背诵九九表到大学学习复变函数和离散数学，看起来好像掌握了这些数学知识，但是在工作中却很少真正用到这些知识，为什么？最近在研究一种开源软件-CARROT2的源代码的时候，又一次感觉到数学在计算机技术中的不可动摇的基础作用，CARROT2是一种用于自动语言分类（聚类）的工具性软件，用JAVA语言编写，它
Linux系统手动安装rzsz 软件包 daizj linux sz rz
1、下载软件 rzsz-3.34.tar.gz。登录linux，用命令 wget http://freeware.sgi.com/source/rzsz/rzsz-3.48.tar.gz下载。 2、解压 tar zxvf rzsz-3.34.tar.gz 3、安装 cd rzsz-3.34 ; make posix 。注意：这个软件安装与常规的GNU软件不
读源码之:ArrayBlockingQueue dieslrae java
ArrayBlockingQueue是concurrent包提供的一个线程安全的队列,由一个数组来保存队列元素.通过 takeIndex和 putIndex来分别记录出队列和入队列的下标,以保证在出队列时不进行元素移动. //在出队列或者入队列的时候对takeIndex或者putIndex进行累加,如果已经到了数组末尾就又从0开始,保证数
C语言学习九枚举的定义和应用 dcj3sjt126com c
枚举的定义 # include <stdio.h> enum WeekDay { MonDay, TuesDay, WednesDay, ThursDay, FriDay, SaturDay, SunDay }; int main(void) { //int day; //day定义成int类型不合适 enum WeekDay day = Wedne
Vagrant 三种网络配置详解 dcj3sjt126com vagrant
Forwarded port Private network Public network Vagrant 中一共有三种网络配置，下面我们将会详解三种网络配置各自优缺点。端口映射(Forwarded port)，顾名思义是指把宿主计算机的端口映射到虚拟机的某一个端口上，访问宿主计算机端口时，请求实际是被转发到虚拟机上指定端口的。Vagrantfile中设定语法为： c
16.性能优化-完结 frank1234 性能优化
性能调优是一个宏大的工程，需要从宏观架构(比如拆分，冗余，读写分离，集群，缓存等)，软件设计（比如多线程并行化，选择合适的数据结构），数据库设计层面（合理的表设计，汇总表，索引，分区，拆分，冗余等）以及微观（软件的配置，SQL语句的编写，操作系统配置等）根据软件的应用场景做综合的考虑和权衡，并经验实际测试验证才能达到最优。性能水很深，笔者经验尚浅，赶脚也就了解了点皮毛而已，我觉得
Word Search hcx2013 search
Given a 2D board and a word, find if the word exists in the grid. The word can be constructed from letters of sequentially adjacent cell, where "adjacent" cells are those horizontally or ve
Spring4新特性——Web开发的增强 jinnianshilongnian spring spring mvc spring4
Spring4新特性——泛型限定式依赖注入 Spring4新特性——核心容器的其他改进 Spring4新特性——Web开发的增强 Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC Spring4新特性——Groovy Bean定义DSL Spring4新特性——更好的Java泛型操作API Spring4新
CentOS安装配置tengine并设置开机启动 liuxingguome centos
yum install gcc-c++ yum install pcre pcre-devel yum install zlib zlib-devel yum install openssl openssl-devel Ubuntu上可以这样安装 sudo aptitude install libdmalloc-dev libcurl4-opens
第14章工具函数（上） onestopweb 函数
index.html <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/
Xelsius 2008 and SAP BW at a glance blueoxygen BO Xelsius
Xelsius提供了丰富多样的数据连接方式，其中为SAP BW专属提供的是BICS。那么Xelsius的各种连接的优缺点比较以及Xelsius是如何直接连接到BEx Query的呢？以下Wiki文章应该提供了全面的概览。 http://wiki.sdn.sap.com/wiki/display/BOBJ/Xcelsius+2008+and+SAP+NetWeaver+BW+Co
oracle表空间相关 tongsh6 oracle
在oracle数据库中，一个用户对应一个表空间，当表空间不足时，可以采用增加表空间的数据文件容量，也可以增加数据文件，方法有如下几种： 1.给表空间增加数据文件 ALTER TABLESPACE "表空间的名字" ADD DATAFILE '表空间的数据文件路径' SIZE 50M; &nb
.Net framework4.0安装失败 yangjuanjava .net windows
上午的.net framework 4.0，各种失败，查了好多答案，各种不靠谱，最后终于找到答案了和Windows Update有关系，给目录名重命名一下再次安装，即安装成功了！下载地址：http://www.microsoft.com/en-us/download/details.aspx?id=17113 方法： 1.运行cmd，输入net stop WuAuServ 2.点击开