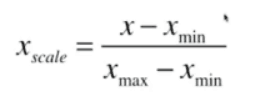机器学习 特征工程及模型聚合
目录
一:什么是特征工程
二:特征工程方法
三:独热编码
四:归一化处理
五:特征工程方法
六:特征工程处理过程
七:Kaggle房价预测实际案例
一:什么是特征工程
1 是最大限度地从原始数据中提取特征以供算法和模型的使用
2 数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限
二:特征工程方法
数据预处理的方式
1 缺失值处理(均值、众数、中位数)
2 字符编码数据处理-亚编码(独热编码)
3 归一化处理
大致过程
数据集准备
数据处理
观察数据是否有特点
数据预处理
构建出数据主要特征
从多列数据中提取出关键的特征
三:独热编码
示例如下
| 是否有朋友 | has_friend_has | has_friend_no |
| 有 | 1 | 0 |
| 没有 | 0 | 1 |
四:归一化处理
简单示例如下,分析问题,天气+价格是特征数据
| 天气10 | 价格 |
| 5 | 50 |
| 3 | 150 |
| 10 | 300 |
| 5 | 140 |
| 5 | 30 |
那么问题如下,天气多云,价格80,是否要出去呢(结果即标签数据)?
| 多云 | 80 | ? |
4-1 最值归一化 normalization
最值归一化:把所有数据映射到0-1之间,如下
适用于分布有明显边界的情况:受outlier影响较大
4-2 均值方差归一化 standardization
数据分布没有明显的边界;有可能存在极端数据值
均值方差归一化:把所有的数据归一到均值为0 方差为1的分布中
x特征
x-mean特征均值
S方差
五:特征工程方法
特征选择
1 特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本没有差异,这个特征对于样本的区分并没有什么用
2 特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优先选择
方差过滤
相关系数
特征降维(特征矩阵过大,导致训练时间太长)
1 主成分分析法PCA,PCA是一种无监督的降维方法
2 现象判别分析法LDA、LDA是一种有监督的降维方法
六:特征工程处理过程
1 空值处理 【数值型(均值、中位数、众数),字符型(众数)】
缺失值超1/3就剔除
2 字符型数据处理--独热编码 将字符型数据转换为数值型数据
3 方差过滤--独热编码形成了非常多新的特征,过滤掉一些列中的数据差别不大的列 <0.1列舍弃
4 相关系数计算(皮尔逊相关系数) 提取主要特征
5 特征构建--查看特征之间的相关系数 若>0.8则剔除其中那一列
6 数据集划分
7 网格模型 超参调优
8 保存模型 预测与实际比对
七:Kaggle房价预测实际案例
from sklearn.impute import SimpleImputer # 众数
from sklearn.preprocessing import OneHotEncoder # 独热编码
from sklearn.feature_selection import VarianceThreshold # 方差过滤
from scipy.stats import pearsonr # 皮尔逊相关系数
import pandas as pd
import numpy as np
# 设置显示所有行、列
pd.set_option("display.max_rows", None)
pd.set_option("display.max_columns", None)
data_df = pd.read_csv("train.csv", sep=',')
# print(data_df.head(), data_df.shape) # 1460*80
# 空值处理
# print(data_df.isnull().sum())
# 超过1/3列的剔除
data_df.drop(columns=['Alley', 'FireplaceQu', 'PoolQC', 'Fence', 'MiscFeature'],
axis=1, inplace=True)
# print(data_df.shape)
# 2 空值填充
# 2-1 [数字列]填充
data_df['LotFrontage'].fillna(data_df['LotFrontage'].mean(), inplace=True)
data_df['GarageYrBlt'].fillna(data_df['GarageYrBlt'].median(), inplace=True)
data_df['MasVnrArea'].fillna(data_df['MasVnrArea'].median(), inplace=True)
# print(data_df.isnull().sum())
# 2-2 剩余的[字符列]在miss_col_list中
# 获取缺失列的名字
miss_col_list = data_df.isnull().any()[data_df.isnull().any().values == True].index.tolist()
# print(data_df.isnull().any())
# print(miss_col_list)
# 获取缺失列对应的列值--list
miss_list = []
for i in miss_col_list:
miss_list.append(data_df[i].values.reshape(-1, 1)) # 任意行 列数为1
# print(miss_list)
# 对每一列进行众数填充
for i in range(0, len(miss_list)):
im_most = SimpleImputer(strategy='most_frequent')
most = im_most.fit_transform(miss_list[i])
data_df.loc[:, miss_col_list[i]] = most
# print(data_df.isnull().sum())
# 目标找到所有的字符列
ob_feature = data_df.select_dtypes(include=['object']).columns.tolist()
# print(ob_feature, len(ob_feature))
ob_df_data = data_df.loc[:, ob_feature]
# print(ob_df_data.head())
# 实例化独热编码对象
OneHot = OneHotEncoder()
# numpy ndarray
result = OneHot.fit_transform(ob_df_data).toarray()
# 获取列名
OneHotNames = OneHot.get_feature_names().tolist()
# print(OneHotNames, len(OneHotNames))
# 独热编码过后的dataframe
OneHot_df = pd.DataFrame(result, columns=OneHotNames)
# print(OneHot_df.head())
# 删除原来的38列字符数据 75-38=37
data_df.drop(columns=ob_feature, inplace=True)
# 行合并 37+234[独热编码出来的新列]=271列+label列=272
data_df = pd.concat([OneHot_df, data_df], axis=1)
# print(data_df.head(), data_df.shape) # (1460, 272)
# feature太多 计算量过大
# 方差过滤
var_index = VarianceThreshold(threshold=0.1)
data = var_index.fit_transform(data_df)
# 获取留下了的索引
index = var_index.get_support(True).tolist()
# print(index)
data_df = data_df.iloc[:, index]
# print(data_df.head(), data_df.shape) # (1460, 84)
# 相关系数分析--皮尔逊相关系数(根据权重)
features = data_df.columns.tolist()
# print(features)
f_names = [] # pearsonr>0.5的列名
# 存储皮尔逊相关系数的值
pear_num = []
# 每一列都要计算与最后一列的pearsonr>0.5
for i in range(0, len(features) - 1):
if abs(pearsonr(data_df[features[i]], data_df[features[-1]])[0]) > 0.5:
f_names.append(features[i])
pear_num.append(pearsonr(data_df[features[i]], data_df[features[-1]])[0])
# print(f_names, len(f_names)) # 13
# 查看特征之间的相关系数
import matplotlib.pyplot as plt
import seaborn as sns
# 根据相关系数的大小--数据封装,封装成DataFrame
pear_dict = {
'features': f_names,
'pearData': pear_num
}
hotPear = pd.DataFrame(pear_dict)
# print(hotPear)
# 皮尔逊相关系数按照从大到小
hotPear.sort_values(by=['pearData'], ascending=False, inplace=True)
# 重置index
hotPear.reset_index(drop=True, inplace=True)
# print(hotPear)
# # 开始绘图
# plt.figure(figsize=(12, 12))
# sns.set(font_scale=0.8)
# cor = np.corrcoef(data_df[f_names].values.T)
# # 数据填充
# sns.heatmap(cor, cbar=False, annot=True, square=True, fmt='0.2f', yticklabels=f_names,
# xticklabels=f_names)
# # plt.show()
# 舍弃相似度高的三列
f_names.append("SalePrice")
data_df = data_df[f_names]
data_df.drop(['GarageArea', 'TotRmsAbvGrd', '1stFlrSF'], inplace=True, axis=1)
# print(data_df.head(), data_df.shape)
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
# 分出feature->array label->array
feature_data = data_df.iloc[:, :-1].values
# print(type(feature_data))
label_data = np.ravel(data_df.iloc[:, -1].values)
# print(label_data,type(label_data))
X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.3, random_state=666)
std = StandardScaler()
X_train_std = std.fit_transform(X_train)
X_test_std = std.fit_transform(X_test)
# print(X_train_std)
# model = KNeighborsRegressor()
# param_list = [
# {
# 'n_neighbors': list(range(1, 38)),
# 'weights': ['uniform']
# },
# {
# 'n_neighbors': list(range(1, 38)),
# 'weights': ['distance'],
# 'p': [i for i in range(1, 21)]
# }
# ]
# grid = GridSearchCV(model, param_grid=param_list, cv=10)
# grid.fit(X_train_std, y_train)
# print(grid.best_score_)
# print(grid.best_params_)
# print(grid.best_estimator_)
# best_model = grid.best_estimator_
best_model = KNeighborsRegressor(n_neighbors=13, p=1, weights='distance')
# 训练模型
best_model.fit(X_train_std, y_train)
# 模型保存
import joblib
joblib.dump(best_model, "PriceRegModel.model")
# 预测
y_predict = best_model.predict(X_test_std)
# 预测与实际 图示点状图
plt.scatter(y_test, y_predict, label="test")
plt.plot([y_test.min(), y_test.max()],
[y_test.min(), y_test.max()],
'k--',
lw=3,
label="predict"
)
plt.show()
预测与实际比对: