房价预测

1、观察大局

寻找数据

UCI
Kaggle

性能指标

均方根误差（RMSE）、平均绝对误差（MAE）
RMSE=sqrt（（（标签向量-预测的标签向量）^2）/实例总数）
MAE=abs（标签向量-预测的标签向量）/实例总数

2、获取数据

下载数据

GitHub
百度云：提取码:78jm

加载数据

使用pandas载入数据集
import pandas as pd

import pandas as pd
housing=pd.read_csv('D:/dataSets/housing.csv')

快速探索数据

绘图 import matplotlib.pyplot as plt
随机抽样 from sklearn.model_selection import train_test_split
分层抽样 from sklearn.model_selection import StratifiedShuffleSplit

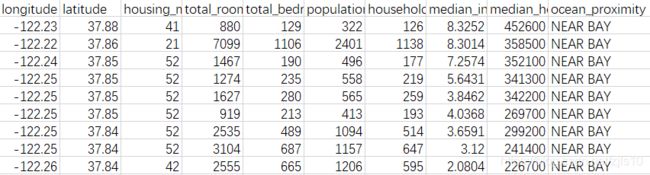
查看前五行

print(housing.head())

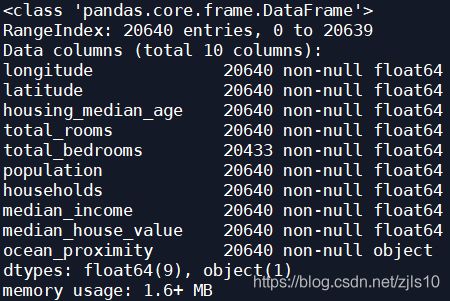
数据集的简单描述

print(housing.info())

对某一属性查看多少种分类

print(housing['ocean_proximity'].value_counts())

数值属性的摘要

print(housing.describe())

• 空值会被省略，故total_bedroom的count是20433
• std是标准差（方差的平方根，测量数值的离散程度）
• longitude的值，25%小于-121.8（第25百分数或第一四分位数），50%小于-118.49（中位数），75%小于-118.01（第75百分数或第三四分位数）

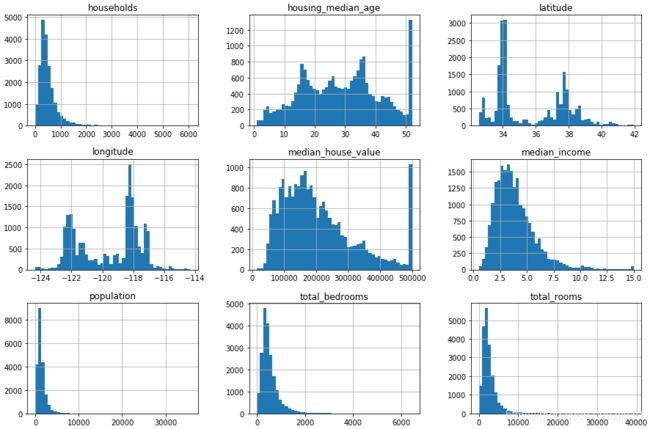
绘制直方图

import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(15,10)) #bin表示有几条柱
plt.show()

创建测试集

纯随机抽样

def split_train_test(data,test_ratio):
    #随机排列组合，打乱index，返回长度为len(data)的一维数组
    shuffled_indices=np.random.permutation(len(data))
    #测试集的样本个数
    test_set_size=int(len(data)*test_ratio)
    #取前A%作为测试集
    test_indices=shuffled_indices[:test_set_size]
    #取剩下的(1-A%)作为训练集
    train_indices=shuffled_indices[test_set_size:]
    #返回训练集与测试集
    return data.iloc[train_indices],data.iloc[test_indices]
#数据集的20%（test_ratio）作为测试集：训练集16512条，测试集4128条
train_set,test_set=split_train_test(housing,0.2) 
print(train_set.head())

为了避免每次运行程序时产生不同的数据集，从而暴露整个完整的数据集，我们需要：
①在运行后即时保存测试集和训练集，随后的运行只是加载它。
②在调用np.random.permutation()之前设置一个随机数种子，如np.random.seed(42)，从而始终产生相同的随机索引。scikit-learn中提供了train_test_split() 函数，能够将数据集分成多个子集，也有random_state参数设置随机数生成种子。

from sklearn.model_selection import train_test_split
#与前面定义的函数几乎相同，但是多了几个额外特征
train_set,test_set=train_test_split(housing,test_size=0.2,random_state=42)
print(train_set.head())

分层抽样

定义：按规定的比例从不同层中抽取样本，从而得到的样本代表性更好，误差更小。每一层要有足够数量的实例，否则其重要程度可能会被错估。

（1）创建五个类别属性

#添加一列新属性：income_cat，希望确保在收入中位数上，测试集能够代表整个数据集中各种不同类型的收入
housing['income_cat']=pd.cut(housing["median_income"],bins=[0.,1.5,3.0,4.5,6.,np.inf],labels=[1,2,3,4,5])
#pd.cut()用来创建5个收入类别属性，1~5作为标签，
#0~1.5是类别1，1.5~3是类别2，以此类推
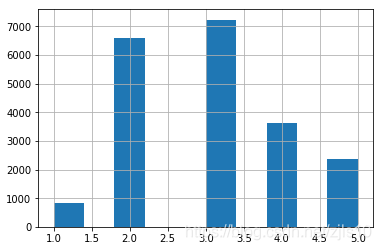
print(housing["income_cat"])
housing["income_cat"].hist()

（2）进行分层抽样

使用sklearn的StratifiedShuffleSplit 类

from sklearn.model_selection import StratifiedShuffleSplit 
#分层抽样，n_splits为数据分成train/test的对数
split=StratifiedShuffleSplit(n_splits=1,test_size=0.2,random_state=42)
#索引值列表train_index、test_index；loc函数表示读取某些行的数据，
#如test1.loc([[1,8,4],[0,1,0]])返回index为1、8、4，column为0、1、0的数据行
for train_index, test_index in split.split(housing,housing["income_cat"]):
    strat_train_set=housing.loc[train_index]
    strat_test_set=housing.loc[test_index]
#可以看到，测试集中收入类别的比例分布和整个数据集很接近
print(strat_test_set["income_cat"].value_counts()/len(strat_test_set))
print(housing["income_cat"].value_counts()/len(housing))

（3）分层抽样结束后删除income_cat属性，将数据恢复原样

drop函数：axis=1时为横轴，表现为列的减少，=0时为纵轴，表现为行的减少；
inplace默认为False，表示是否替换原数组

for set_ in(strat_train_set, strat_test_set): #删除income_cat属性
    set_.drop("income_cat",axis=1,inplace=True)

3、数据可视化

绘图 import matplotlib.pyplot as plt
计算皮尔逊r采用corr()方法
绘制每个数值属性相对于其他数值属性的相关性 from pandas.plotting import scatter_matrix

• 先把测试集放在一边，只能探索训练集

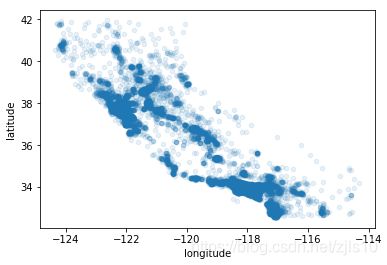
地理数据可视化

housing=strat_train_set.copy() #训练集副本，避免损害训练集
#散点图scatter，横坐标x，纵坐标y，alpha透明度（可清楚看到高密度数据点的位置），子图用legend
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.1) #房子数量与经纬度的关系
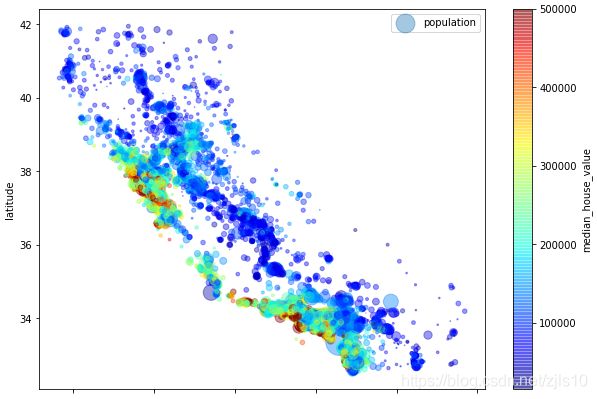
#label图例，figsize图像尺寸，每个圆的半径s大小代表每个区域的人口数量，颜色c代表价格
#颜色表cmap采用jet，从低到高为蓝到红（gray_r为黑白）
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.4,s=housing["population"]/50,label="population",figsize=(10,7),c="median_house_value",cmap=plt.get_cmap("jet"),colorbar=True) #房价、人口与经纬度的关系
plt.legend()

寻找相关性

#corr()计算出每对属性之间的标准相关系数（皮尔逊r）
corr_matrix=housing.corr() 
#每对属性之间的标准相关系数，-1~1，越接近1越正相关，越接近-1越负相关
print(corr_matrix["median_house_value"].sort_values(ascending=False)) 
#每个属性与房价中位数的相关性
housing.plot(kind="scatter",x="median_income",y="median_house_value",alpha=0.1) 
#查看房价中值和收入中值的相关性的散点图

由上图可以看到，二者相关性较强，点并不是很分散且明显呈上升趋势。

#绘制每个数值属性相对于其他数值属性的相关性
from pandas.plotting import scatter_matrix
attributes=["median_house_value","median_income","total_rooms","housing_median_age"]
scatter_matrix(housing[attributes],figsize=(12,8))

当pands绘制每个变量对于自身的图像，主对角线将都是直线，这样毫无意义。因此取而代之，显示了每个属性的直方图。

添加不同属性的组合

• 在给机器学习算法输入数据之前，不仅需要提前清理掉异常数据，同时也会发现不同属性之间的有趣联系。包括尝试各种属性的组合以及对它们进行转换处理 (例如取对数) 等。

#房间总数/家庭数
housing["rooms_per_household"]=housing["total_rooms"]/housing["households"]
#卧室总数/房间总数
housing["bedrooms_per_room"]=housing["total_bedrooms"]/housing["total_rooms"]
#每个家庭的人口数
housing["population_per_household"]=housing["population"]/housing["households"]
#查看相关矩阵
corr_matrix=housing.corr() 
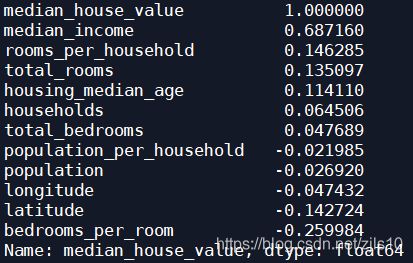
#按相关性递减显示
print(corr_matrix["median_house_value"].sort_values(ascending=False))

4、数据准备

处理部分缺失值：DataFrame的dropna()、drop()、fillna()方法
转换流水线：

再次拷贝strat_train_set，回到干净的数据集，然后将预测器和标签分开

#这里drop会创建一个数据副本但是不影响strat_train_set
housing =strat_train_set.drop("median_house_value",axis=1)
housing_labels=strat_train_set["median_house_value"].copy()

数据清理

前面我们注意到total_bedrooms属性有部分值缺失，我们有三种方法解决：
①放弃这些区域
②放弃整个属性
③用某个值填充（0、平均数、中位数等）

from sklearn.impute import SimpleImputer
imputer使用fit()将imputer实例适配到训练数据，再用transform()将缺失值替换成中位数值
from sklearn.preprocessing import OneHotEncoder
独热编码，类别与自己相等时为1，其余为0。因此返回一个稀疏矩阵
from sklearn.preprocessing import OrdinalEncoder
在这里可以将类别从文本转到数字，一定情况下，两个相近的值说明二者更为相似。这里显然不适合用这方法
from sklearn.base import BaseEstimator, TransformerMixin
自定义转换器，这里用了一个简单的转换器类，来添加前面提到过的组合属性
from sklearn.pipeline import Pipeline
转换流水线
from sklearn.preprocessing import StandardScaler
估算器，配合流水线
from sklearn.compose import ColumnTransformer
分别处理类别列和数值列

使用pandas

housing.dropna(subset=["total_bedrooms"])    #option1
housing.drop("total_bedrooms",axis=1)        #option2
#计算出训练集的中位数然后用它填充缺失值
medians=housing["total_bedrooms"].medians()  #option3
housing["total_bedrooms"].fillna(median,inplace=True)

使用sklearn

from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import OrdinalEncoder
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
housing_num=housing.drop("ocean_proximity",axis=1) #取数据集的数字部分
#双中括号：单列聚合时输出带有列标签，多列聚合时无区别
housing_cat=housing[["ocean_proximity"]] #取数据集的文本部分（ocean列数据）
cat_encoder=OneHotEncoder()
housing_cat_1hot=cat_encoder.fit_transform(housing_cat)

rooms_ix,bedrooms_ix, population_ix,households_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
    def __init__ (self, add_bedrooms_per_room = True): # no *args or **kargs
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self, X, y=None):
        return self# nothing else to do
    def transform(self, X):
        rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
        population_per_household = X[:, population_ix] / X[:, households_ix]
        if self.add_bedrooms_per_room:
            bedrooms_per_room = X[: , bedrooms_ix] / X[ :, rooms_ix]
            return np.c_[X, rooms_per_household, population_per_household ,bedrooms_per_room ]
        else:
            return np.c_[X, rooms_per_household, population_per_household]
num_pipeline =Pipeline([('imputer',SimpleImputer(strategy="median")),('attribs_adder',CombinedAttributesAdder()),('std_scaler',StandardScaler())])

num_attribs=list(housing_num)
cat_attribs=["ocean_proximity"]
full_pipeline=ColumnTransformer([("num",num_pipeline,num_attribs),("cat",OneHotEncoder(),cat_attribs)])
housing_prepared=full_pipeline.fit_transform(housing)
print(housing_prepared)

流水线返回的是numpy数组。若想转回pandasDataFrame，可以做以下操作：

a=np.append(num_attribs,["rooms_per_household","population_per_household","bedrooms_per_room"])
##cat_encoder.categories_返回独热编码的每一个column
a=np.append(a,cat_encoder.categories_) 
##返回的numpy数组转回pandas
test=pd.DataFrame(housing_prepared,columns=a) 
print(test)

pandas转numpy：housing.values 即可

5、选择并训练模型

线性回归：from sklearn.linear_model import LinearRegression
决策树：from sklearn.tree import DecisionTreeRegressor
对模型验错：from sklearn.metrics import mean_squared_error
交叉验证法：from sklearn.model_selection import cross_val_score

线性回归

from sklearn.linear_model import LinearRegression
lin_reg=LinearRegression()
lin_reg.fit(housing_prepared,housing_labels)#训练线性回归模型

some_data=housing.iloc[:5]#取前五个数据
some_labels=housing_labels.iloc[:5]#去前五个结果
some_data_prepared=full_pipeline.transform(some_data)#流水线处理前五行数据
print("predictions:",lin_reg.predict(some_data_prepared))#预测
print("labels:",list(some_labels))

验错

from sklearn.metrics import mean_squared_error#用这个模型对整个训练集验错
housing_predictions=lin_reg.predict(housing_prepared)#预测值
lin_mse=mean_squared_error(housing_labels,housing_predictions)
lin_rmse=np.sqrt(lin_mse)
print(lin_rmse)

10折交叉验证

lin_scores=cross_val_score(lin_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
lin_rmse_scores=np.sqrt(-lin_scores)#10折交叉验证线性回归
display_scores(lin_rmse_scores)

决策树

from sklearn.tree import DecisionTreeRegressor
tree_reg=DecisionTreeRegressor() #决策树
tree_reg.fit(housing_prepared,housing_labels) #训练决策树模型

验错

housing_predictions=tree_reg.predict(housing_prepared)
tree_mse=mean_squared_error(housing_labels,housing_predictions)
tree_rmse=np.sqrt(tree_mse)
print(tree_mse) #训练集评估无错误，可能过拟合

10折交叉验证

from sklearn.model_selection import cross_val_score #交叉验证法
tree_scores=cross_val_score(tree_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
tree_rmse_scores=np.sqrt(-tree_scores) #10折交叉验证决策树
print(tree_rmse_scores)

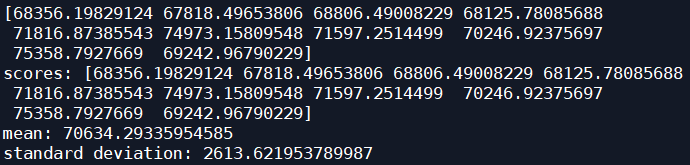
def display_scores(scores):
    print("scores:",scores)#十次评估分数的数组
    print("mean:",scores.mean())#评分
    print("standard deviation:",scores.std())#上下浮动
display_scores(tree_rmse_scores)#严重过拟合

随机森林

from sklearn.ensemble import RandomForestRegressor
forest_reg=RandomForestRegressor()
forest_reg.fit(housing_prepared,housing_labels)

housing_predictions=forest_reg.predict(housing_prepared)

验错

forest_mse=mean_squared_error(housing_labels,housing_predictions)
forest_rmse=np.sqrt(forest_mse)
print(forest_rmse)

10折交叉验证

forest_scores=cross_val_score(forest_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
forest_rmse_scores=np.sqrt(-forest_scores)#10折交叉验证决策树
display_scores(forest_rmse_scores)

6、微调模型

网格搜索

from sklearn.model_selection import GridSearchCV
param_grid=[
        {'n_estimators':[3,10,30],'max_features':[2,4,6,8]},
        {'bootstrap':[False],'n_estimators':[3,10],'max_features':[2,3,4]}
    ]
forest_reg=RandomForestRegressor()
grid_search=GridSearchCV(forest_reg,param_grid,cv=5,
                         scoring='neg_mean_squared_error',
                         return_train_score=True)
grid_search.fit(housing_prepared,housing_labels)
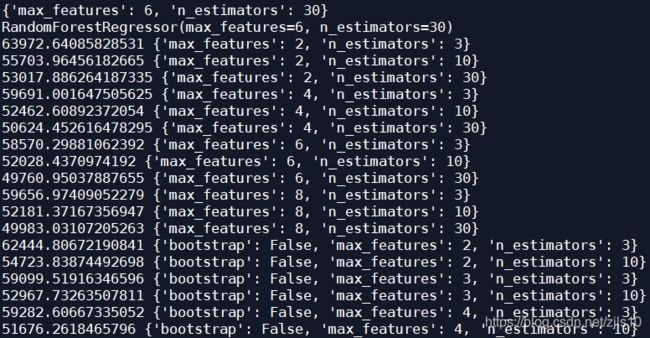
print(grid_search.best_params_)
print(grid_search.best_estimator_)
cvres=grid_search.cv_results_
for mean_score,params in zip(cvres["mean_test_score"],cvres["params"]):
    print(np.sqrt(-mean_score),params)

随机搜索

当超参数的搜索范围较大时，通常优先选择RandomizedSearchCV。
它不会尝试所有可能的组合，而是在每次迭代中选择一个随机值作为超参数。

分析最佳模型以及误差

Random-ForestRegressor可以指出每个属性的相对重要程度

a=[1,2,3]
b=[4,5,6]
zip(a,b)=[(1,4),(2,5),(3,6)]

feature_importances=grid_search.best_estimator_.feature_importances_
print(feature_importances)
extra_attribs=["rooms_per_hhold","pop_per.hhold","bedrooms_per_room"]
cat_encoder=full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs=list(cat_encoder.categories_[0])
attributes=num_attribs+extra_attribs+cat_one_hot_attribs
print(sorted(zip(feature_importances,attributes),reverse=True))

7、通过测试集评估

在测试集上评估最终模型

final_model=grid_search.best_estimator_

x_test=strat_test_set.drop("median_house_value",axis=1)
y_test=strat_test_set["median_house_value"].copy()

x_test_prepared=full_pipeline.transform(x_test)
final_predictions=final_model.predict(x_test_prepared)

final_mse=mean_squared_error(y_test,final_predictions)
final_rmse=np.sqrt(final_mse)
print(final_rmse)

泛化误差显然比一开始的线性回归小很多了

计算泛化误差的95%置信区间

from scipy import stats
confidence=0.95
squared_errors=(final_predictions-y_test)**2
print(np.sqrt(stats.t.interval(confidence,len(squared_errors)-1,
                         loc=squared_errors.mean(),
                         scale=stats.sem(squared_errors))))

泛化误差有95%的可能性落在这个区域内：