常见的k临近向量检索算法

今天要讲博客博客都围绕一个问题主题展开：有一个包含了N个元素的集合，在向量化的参数空间里，给出任何一个节点i，如何在最短的时间复杂度的前提下找到该节点$i$的$k$临近向量子集。

当然第一直觉是最少也要把元素$i$和集合里其余$N-1$个元素两两比较，这样才能从这$N-1$个元素中找到k个最大的元素。当然如果在N不是特别大的时候，这种方法也是可以的。但是如果是类似应用在搜索推荐系统的召回环节，往往候选集规模在千万量级，这种全部遍历的方法往往效率就不够了。这时候就需要对检索结构进行特殊的设计，甚至在一定程度上会牺牲部分“计算精度”来换取“检索时间”。今天准备将几种在工业界中使用的比较多的算法模型。（PS：今天的博客更侧重于从“what”和“how”这个角度来进行介绍，更多“why”等维度的内容会在未来抽空总结介绍）

HNSW检索框架

这种框架是目前比较火的向量k临街检索框架之一，阿里的“二向箔”检索技术就是在该框架的基础之上构建起来的。
其实HNSW(Hierarchcal Navigable Small World graphs)是NSW( Navigable Small World graphs)算法在高维空间的扩展版本，可以在NSW算法的基础上理解HNSW算法。

上图是NSW算法的构图结构。
为了加快k临街节点的搜索效率，首先需要构建一张图。这种图中每一个点代表了一个数据点，数据点会和自己最多$M$个最近的邻居之间有边相连(M为构图流程中的超参数，用来权衡搜索过程的精度和速度)，这些邻居节点也称之为“友点”：

构图之后需要保证：
1 所有数据向量节点都必须有友点；（必选项）
2 每个节点的友点个数最多不超过M个；（必选项）
3 距离相近的点最好互为“友点”；（必选项）（PS:无向图天然就满足这点）
4 最好有高速公路机制，可以加快搜索速度。（可选项）

知道了这个图的需要满足的性质，那么在得到图后如何检索距离某一个query节点(图中绿色节点)的k临近节点呢，下面来讲解一下这个搜索检索过程：（后续的构图过程也依赖该流程）
1 随机从图中选择一个节点作为enter point；
2 从计算enter point节点以及其友点和 query之间的距离，并把top n(n一般大于等于k)节点存入中间结果动态缓存列表中；同时在查找的过程中，为了提高效率，我们可以建立一个废弃列表，在一次查找任务中遍历过的点不再遍历。
3 根据中间结果动态缓存列表中的结果，并行地对这n个点进行同时计算“友点”（前提是这些友点没有在废弃列表中出现）和待查找点的距离，在这些“友点”中选择n个点与动态列表中的n个点进行并集操作，在并集中选出n个最近的友点，更新动态列表和废弃列表；
4 当根据中间结果无法继续扩展出新的节点的时候，整个算法结束。取动态列表中的top s元素即可作为最终的检索结果。

在了解了基于NSW算法的top S检索策略之后，那么整个构图的流程就更简单了：
向图中逐个插入点，插图一个全新点时，通过朴素想法中的朴素查找法（通过计算“友点”和待插入点的距离来判断下一个进入点是哪个点）查找到与这个全新点最近的m个点（m由用户设置），连接全新点到m个点的连线。（PS：但是在节点插入环节有一个细节需要注意下，由于连接的边是无向的。在当前节点和m个临近节点在进行连边操作的时候，有可能会导致这m个临近节点中的某一个节点u的临邻居会超过m个约束。这时候就需要将u的m+1个临近节点全部拿出来按照距离u的距离进行排序，只保留前m个节点的边）

上述构图过程虽然看着简单，但其实仔细思考的话，是能够满足上面的几个必选项和那一个可选项的。同时如果对整个流程熟悉的话，会发现“高速公路机制”的连边往往会在构图的早期生成。

上面讲解完了NSW，在讲HNSW之前，可以先了解一种数据结构：跳表。

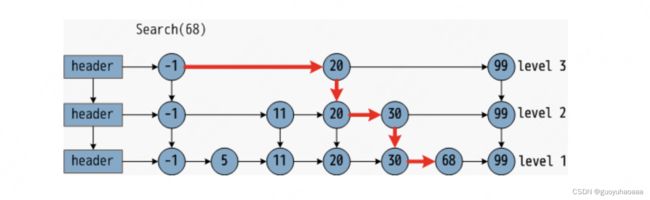
图中的跳表的底层level 1 是原始的明细数据层，上面的level 2 和level 3分别是“索引”层。假设原始数据序列是按照顺序并且底层的数据结构采用的是链表这种链式的访问结构的话，使用跳表，尤其是整个结构中的层和层之间的“跳转”能够大大的节约跳转时间。
如果理解了跳表的结构和工作原理，再加上对NSW工作流程的熟悉。那么对HNSW=NSW+跳表。

上图就是HNSW的模型结构示意图，其中layer 1 ，layer 2 和 layer 3每一层都可以看做是NSW，最底层的Layer 0中的节点包含了所有图中的节点，layer 1 和layer 2只包含了图中的一部分节点。同时从图中不难看出，layer 2 的节点数量比layer 1的节点数量更少。

至于每一个节点最多能够到达第几层，是按照公式$P=floor(-ln(uniform(0,1))\ast layerNum)$算出来的。该公式的执行每一次之间都是独立的。

这样在插入的过程中，针对目标待插入节点u。可以先计算得到其最终能够到达的最大层次，然后在每一层能够到达的层次中按照NSW的算法进行节点的插入。检索过程如下所示：

但是这里有一点可能需要注意的是，为了避免构造的图产生local minimum现象，降低搜索效率：

在从中间结果动态缓存列表中选择top r元素作为邻居的时候:
假设当前出队的是节点A，x为待搜索query。最终的结果集合是R，初始化为空。
对于R中任意一个节点n，如果dist(A,n) < dist(A,x)，说明节点A和已有的结果集中的节点离的太近了，这样的节点会被丢弃，正如上文所说，要避免只有邻近的cluster被选中做邻居。
如果R中的每个节点都和A离的比较远的话，A就可以进入R了。
当然这样的做法可能会导致过滤得到的合适节点数量小于目标值r。算法会在最后加一个兜底策略，从那些被淘汰掉的节点集合中选择距离x更近的进行补充。

基于HNSW算法的好处是泛化能力强，整个算法框架可以灵活的和各种距离计算函数（甚至是复杂的NN打分模型）进行结合，非常方便。

PQ检索框架

所谓PQ即为Product quantization(乘积量化)的简写。facebook著名的开源框架faiss就用了该方法进行加快检索。(PS：faiss库中另一个向量降维的方法为PCA)。

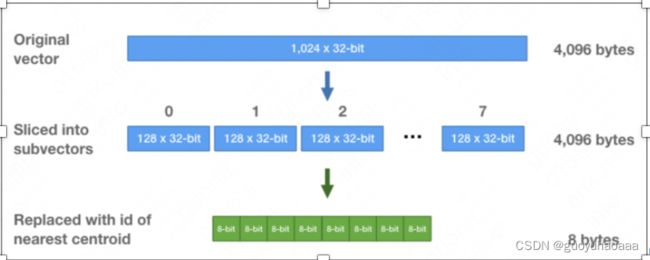
PQ是一种建立索引的方式，假设原始向量是1024维，可以把它拆解成8个子向量，每个子向量128维。对于这8组子向量的每组子向量，使用 kmeans 方法聚成k=256类。也就是说，每个子向量有256个中心点(centroids)。如下图。

在product quantization方法中，这256个中心点构成一个码本。这些码本的笛卡尔积就是原始D维向量对应的码本。这样在计算两个向量$vecto{r}_A$和$vecto{r}_B$的距离的时候，可以按照向量维度进行分成8段，分别计算两个向量不同分段对应中心点的码本距离，然后将8段得到的码本距离加和就得到了最终向量A和向量B的近似距离。

注意到每组子向量有其256个中心点，我们可以中心点的 ID 来表示每组子向量中的每个向量。中心点的 ID只需要 8位(=$lo{g}_{2}256$)来保存即可。这样，初始一个由32位浮点数组成的1,024维向量，可以转化为8个8位整数组成。如下图。

对向量压缩后，有2种方法作相似搜索。一种是SDC(symmetric distance computation)，另一种是ADC(asymmetric distance computation)。SDC算法和ADC算法的区别在于是否要对查询向量x做量化，参见公式1和公式2。如下图所示，x是查询向量(query vector)，y是数据集中的某个向量，目标是要在数据集中找到x的相似向量。

SDC算法：先用PQ量化器对x和y表示为对应的中心点q(x)和q(y)，然后用公式1来近似d(x,y)。这里 q 表示 PQ量化过程。

ADC算法：只对y表示为对应的中心点q(y)，然后用下述公式2来近似d(x,y)。

KD-Tree检索框架

kd（k-dimensional）树的概念自1975年提出，试图解决的是在k维空间为数据集建立索引的问题。依上文所述，已知样本空间如何快速查询得到其近邻？唯有以空间换时间，建立索引便是计算机世界的解决之道。但是索引建立的方式各有不同，kd树只是是其中一种。它的思想如同分治法，即：利用已有数据对k维空间进行切分。该算法在sikit-learn中的KNN算法中有所使用。

其实整个kd树的构造流程还是比较简洁的，整体结构可以表现为一颗二叉树：

针对每一个节点内的数据，计算k个维度中每一个维度数据的方差，选取方差最大的维度为分裂维度（PS：方差值越大说明数据在该维度上越分散，则更适合用来作为分裂的维度）。然后将数据按照该目标维度取值进行排序，选择排序后的目标中间值作为节点分裂值。

值得注意的是，在kd树的实现过程中，切分域的选择并不一定采用方差选择方式，而可能只是简单的以 d mod n 维度的方式，来决定该层树的切分域（d代表树节点的深度，n代表维度数量，求模来确定切分域）。这样实现简单，效果也一般不会太差。

其查找过程如下所示：
1 寻找近似点-寻找最近邻的叶子节点作为目标数据的近似最近点。
2 回溯-以目标数据和最近邻的近似点的距离沿树根部进行回溯和迭代。

由于整个KD-Tree的构建过程和查找过程比较清晰简单，符合直觉，这里就不再赘述。具体的其他相关细节可以看：https://zhuanlan.zhihu.com/p/53826008。

但从上面三个算法本身来看。HNSW模型框架本身并没有和任何一种距离计算范式耦合，能够支持任意定制的距离计算函数。而Product quantization和KD-Tree框架本身和欧式距离的计算范式耦合较为紧密。个人感觉在一定程度上限制了算法模式的应用场景。