『ML』用Python实现聚类效果的评估(轮廓系数、互信息)
好的聚类:类内凝聚度高,类间分离度高。
本文介绍两种聚类评估方法,轮廓系数(Silhouette Coefficient)以及标准化互信息(NMI),并且用Python实现。
关于K-Means聚类请看 利用K-Means聚类算法对未标注数据分组
导航
- 效果评估综述
- 轮廓系数
- 互信息
- 参考文章
效果评估综述
这里直接贴上 聚类算法初探(七)聚类分析的效果评测
它摘自于中国科学院计算技术研究所周昭涛的硕士论文《文本聚类分析效果评价及文本表示研究》的第三章。建议先看看原文,可以对聚类评估有一个很好的了解。
综合来说,我们希望最终的聚类结果是:同一个簇内的点是紧密的,而不同簇之间的距离是较远的;同时,它也要与我们人工的判断相一致。
接下来介绍两种聚类评估方法:轮廓系数和标准化互信息。前者是无需数据标注,判断聚类的 类内距 和 类间距 ;而后者是需要对于数据进行 标注 ,判断聚类的 准确性 。
轮廓系数
在聚类时,如果 类别未知 时,可以选择轮廓系数作为聚类性能的评估指标。从 百度百科 摘取的轮廓系数的介绍:
轮廓系数是聚类效果好坏的一种评价方式。它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。
以K-Means举例。由于 k k k 的值是需要事先给定的。如果我们不太清楚数据分几个簇比较好,我们可以尝试用不同的 k k k 值来计算轮廓系数,从而选择 最优 的一个 k k k 值。计算过程如下:
- 对于一个簇中的一个点 i i i
- a a a ( i i i ) = a v e r a g e average average ( i i i 向量到所有它属于的簇中其它点的距离 )
- b b b ( i i i ) = m i n min min ( i i i 向量到与它相邻最近的一簇内的所有点的平均距离 )
- 那么 i i i 的轮廓系数为 S ( i ) = ( b ( i ) − a ( i ) ) / m a x { a ( i ) , b ( i ) } S(i)=( b(i)-a(i) ) / max\{ a(i),b(i) \} S(i)=(b(i)−a(i))/max{a(i),b(i)}
- 将所有点的轮廓系数求平均,就是该聚类结果总的轮廓系数。
其中, a a a ( i i i ) 可以理解为一点与簇内其他点不相似性的平均值,即类内的 凝聚度 ; b b b ( i i i ) 可以理解为一点与最近簇的不相似性的平均值,即类间的 分离度 。
我们也可以看到, S ( i ) S(i) S(i) 是介于[-1, 1]之间的。 a a a ( i i i ) 越小, b b b ( i i i ) 越大,说明聚类效果越好,轮廓系数 S ( i ) S(i) S(i) 就越接近1。
那么,如果用Python来实现呢?给出它的伪代码:
输入:数据的个数m,k的取值范围
输出:每个k所对应的轮廓系数
在取值范围内的每一个k:
对于每一个簇:
对于每一个点i:
计算i与簇内其他点距离之和的平均值,记为a(i)
计算i与其他簇每个点距离之和的平均值,选择最小的那一个,记为b(i)
s(i) = (b(i)-a(i)) / max(a(i), b(i))
加总每一个点的轮廓系数,记为 sum
轮廓系数 s = sum / m
接下来用代码实现,K-Means 具体细节可以参考 利用K-Means聚类算法对未标注数据分组。
因此,运行K-Means的代码我就不贴啦,我就直接附上轮廓系数的代码。代码中的一些细节在上面的博客中得到了解释,有什么疑问可以先看看那篇博文哦。
首先,我的数据集为testSet.txt,运行 K-Means 的代码为biKMeans(data, k), d a t a data data 为传入的数据集矩阵, k k k 是簇的个数。这个函数返回两个值,一个是中心点,另一个是clusterAssment,它一共有 m m m 行( m m m 为数据集的行数),两列,第一列保存这一点所在簇的索引,第二列保存到簇中心距离的平方。
if __name__ == '__main__':
data = np.mat(loadDataSet('testSet.txt'))
m = np.shape(data)[0] # 一共有m行数据
for k in range(2, 10): # 簇的个数取值在2到9之间
clusterAssment = biKMeans(data, k)[1] # 进行二分类,返回保存簇索引的矩阵
s_sum = 0 # 所有簇的s值
cluster_s = 0 # 一个簇所有点的的s值
for cent in range(k): # 对于每一个簇
category = np.nonzero(clusterAssment[:, 0] == cent)[0] # 得到簇索引为cent的值的位置,形式类似为[1, 4 ,6]
clusterNum = len(category) # 该簇中点的个数
s = 0
for index, lineNum in enumerate(category): # 对于簇中的每一个点,index为索引,lineNum为点所在的行数
# 计算该点到簇内其他点的距离之和的平均值
innerSum = 0
for i in range(clusterNum):
if i == index:
continue # 若为当前该点,则跳出本次循环
dis = distCal(data[category[i]], data[lineNum]) # 若二者为不同点,计算二者之间的距离
innerSum += dis # 将之保存到内部距离
a = innerSum / clusterNum
# 计算该点到其他簇所有点距离之和的最小平均值
minDis = np.inf # 设定初始最小值为无穷大
for other_cent in range(k): # 对于每一个簇
if other_cent != cent: # 如果和上面给定的簇不一样
other_category = np.nonzero(clusterAssment[:, 0] == other_cent)[0] # 得到簇里面点对应的行数
other_clusterNum = len(other_category) # 该簇中点的个数
other_sum = 0
for other_lineNum in other_category: # 对于簇中的每一个点
other_dis = distCal(data[other_lineNum], data[lineNum])
other_sum += other_dis
other_sum = other_sum / other_clusterNum # 求平均
if other_sum < minDis:
minDis = other_sum # 如果一个点距离另外一个簇所有点的距离小于当前最小值,则更新
b = minDis
s += (b-a) / max(a, b) # 每一个点的轮廓系数
cluster_s += s # 每一个簇的s值
s_sum = cluster_s / m # 取平均
print("当前k的值为:%d" % k)
print("轮廓系数为:%s" % str(s_sum))
print('***' * 20)
我的数据集一共有80行,可以看到我的 k k k 取值范围在[2, 10),最终打印的结果如下:
注意:对于簇结构为凸的数据轮廓系数值高,而对于簇结构非凸需要使用DBSCAN进行聚类的数据,轮廓系数值低,因此,轮廓系数 不应该 用来评估 不同聚类算法 之间的优劣,比如Kmeans聚类结果与DBSCAN聚类结果之间的比较。
画出图来,发现的确是 k = 4 k=4 k=4 的效果比较好!
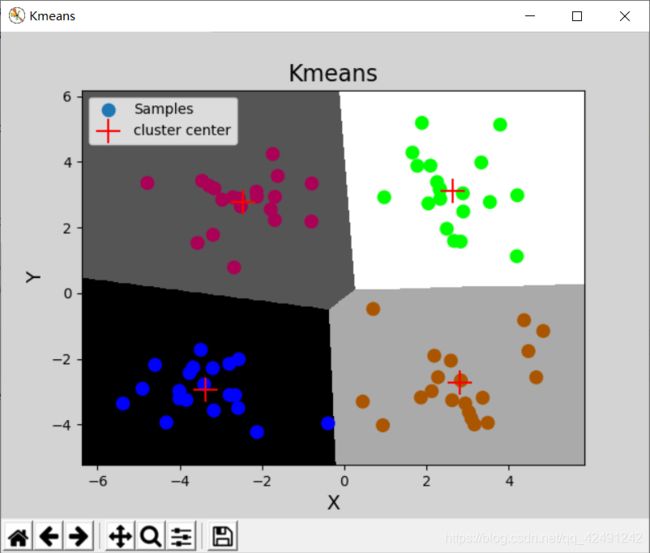
画图的代码是用sklearn做的,请看原文博主:sklearn之聚类评估指标—轮廓系数。
还是贴出代码吧!sklearn有现成的函数可以调用,就不用写轮廓系数的代码啦!很方便的!
import numpy as np
import matplotlib.pyplot as mp
import sklearn.cluster as sc
import sklearn.metrics as sm
# 读取数据,绘制图像
x = np.loadtxt('testSet.txt', unpack=False, dtype='f8', delimiter='\t')
print(x.shape)
# 基于Kmeans完成聚类
model = sc.KMeans(n_clusters=4)
model.fit(x) # 完成聚类
pred_y = model.predict(x) # 预测点在哪个聚类中
print(pred_y) # 输出每个样本的聚类标签
# 打印轮廓系数
print(sm.silhouette_score(x, pred_y, sample_size=len(x), metric='euclidean'))
# 获取聚类中心
centers = model.cluster_centers_
print(centers)
# 绘制分类边界线
l, r = x[:, 0].min() - 1, x[:, 0].max() + 1
b, t = x[:, 1].min() - 1, x[:, 1].max() + 1
n = 500
grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n))
bg_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
bg_y = model.predict(bg_x)
grid_z = bg_y.reshape(grid_x.shape)
# 画图显示样本数据
mp.figure('Kmeans', facecolor='lightgray')
mp.title('Kmeans', fontsize=16)
mp.xlabel('X', fontsize=14)
mp.ylabel('Y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray')
mp.scatter(x[:, 0], x[:, 1], s=80, c=pred_y, cmap='brg', label='Samples')
mp.scatter(centers[:, 0], centers[:, 1], s=300, color='red', marker='+', label='cluster center')
mp.legend()
mp.show()
互信息
这里会涉及到一些 熵 的知识,建议看这位博主写的 信息论基础 。
这里仍然参考了百度百科 互信息 。
互信息 (Mutual Information) 是信息论里一种有用的信息度量,它可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。
当信源发出一个信息 x x x 时,由于通道往往会有噪音和干扰,使得信宿往往接受到的是变形的 y y y 。 y y y 收到后推测由 x x x 发出的概率,称为后验概率;而信源发出 x x x 的概率,我们称为先验概率。定义 x x x 的后验概率与先验概率比值的对数为 y y y 对 x x x 的互信息量(简称互信息)。
我们看如何计算,首先是熵的计算公式:
H ( X ) = ∑ x p ( x ) log 1 p ( x ) H(X)=\sum_{x} p(x)\log \frac{1}{p(x)} H(X)=x∑p(x)logp(x)1
由熵的连锁规则:
H ( X , Y ) = H ( X ) + H ( Y ∣ X ) = H ( Y ) + H ( X ∣ Y ) H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y) H(X,Y)=H(X)+H(Y∣X)=H(Y)+H(X∣Y)
所以:
H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) H(X)-H(X|Y)=H(Y)-H(Y|X) H(X)−H(X∣Y)=H(Y)−H(Y∣X)
这个差值就是随机变量 ( X , Y ) (X,Y) (X,Y) 是互信息。
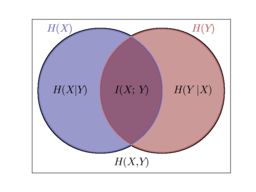
可以这样理解: H ( X ) H(X) H(X) 是 X X X 变量的不确定性, H ( X ∣ Y ) H(X|Y) H(X∣Y) 是知道了 Y Y Y 之后, X X X 的不确定性, H ( X ) − H ( X ∣ Y ) H(X)-H(X|Y) H(X)−H(X∣Y) 就是由于知道 Y Y Y 而使得 X X X 不确定性减少 的量(即 Y Y Y 透露了多少 X X X 的信息?),这部分就是 互信息 。
I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) I(X;Y)=H(X)-H(X|Y) I(X;Y)=H(X)−H(X∣Y) = H ( X ) + H ( Y ) − ( H ( Y ) + H ( X ∣ Y ) ) =H(X)+H(Y)-(H(Y)+H(X|Y)) =H(X)+H(Y)−(H(Y)+H(X∣Y)) = H ( X ) + H ( Y ) − H ( X , Y ) =H(X)+H(Y)-H(X,Y) =H(X)+H(Y)−H(X,Y) = ∑ x p ( x ) log 1 p ( x ) + ∑ y p ( y ) log 1 p ( y ) − ∑ x , y p ( x , y ) log 1 p ( x , y ) =\sum_{x} p(x)\log \frac{1}{p(x)}+\sum_y p(y)\log \frac{1}{p(y)}-\sum_{x,y} p(x,y)\log \frac{1}{p(x,y)} =x∑p(x)logp(x)1+y∑p(y)logp(y)1−x,y∑p(x,y)logp(x,y)1 = ∑ x , y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) =\sum_{x,y}p(x,y)\log \frac {p(x,y)}{p(x)p(y)} =x,y∑p(x,y)logp(x)p(y)p(x,y)
这个就是互信息的计算公式。那么如何运用到聚类中呢?举一个例子,这里参考了 标准化互信息NMI计算步骤及其Python实现 。
总共有6个数据点。 A A A 是经过某种算法聚类后,得到的结果; B B B 是标准的聚类结果,是由人工标注数据得到的。
A = [ 0 , 0 , 1 , 0 , 1 , 0 ] A = [0, 0, 1, 0, 1, 0] A=[0,0,1,0,1,0]
B = [ 0 , 0 , 0 , 1 , 1 , 1 ] B = [0, 0, 0, 1, 1, 1] B=[0,0,0,1,1,1]
我们发现, A A A、 B B B 都将数据聚成了两类: X = u n i q u e ( A ) = { 0 , 1 } X=unique(A)=\{0,1\} X=unique(A)={0,1}, Y = u n i q u e ( B ) = { 0 , 1 } Y=unique(B)=\{0,1\} Y=unique(B)={0,1},由 M I MI MI 的计算公式:
M I ( X , Y ) = ∑ x ∑ y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) MI(X,Y)=\sum_{x}\sum_{y}p(x,y)\log \frac {p(x,y)}{p(x)p(y)} MI(X,Y)=x∑y∑p(x,y)logp(x)p(y)p(x,y)
首先计算联合概率分布:
P ( 0 , 0 ) = 2 6 P(0,0)=\cfrac{2}{6} P(0,0)=62 P ( 0 , 1 ) = 2 6 P(0,1)=\cfrac{2}{6} P(0,1)=62
P ( 1 , 0 ) = 1 6 P(1,0)=\cfrac{1}{6} P(1,0)=61 P ( 1 , 1 ) = 1 6 P(1,1)=\cfrac{1}{6} P(1,1)=61
再分别计算各自的概率分布:
对于 A A A, P A ( 0 ) = 4 6 P_{A}(0)=\cfrac{4}{6} PA(0)=64 P A ( 1 ) = 2 6 P_{A}(1)=\cfrac{2}{6} PA(1)=62
对于 B B B, P B ( 0 ) = 3 6 P_{B}(0)=\cfrac{3}{6} PB(0)=63 P B ( 1 ) = 3 6 P_{B}(1)=\cfrac{3}{6} PB(1)=63
即可计算出 M I MI MI 的值。
要对计算的值进行归一化,公式为:
N M I ( X , Y ) = 2 M I ( X , Y ) H ( X ) + H ( Y ) NMI(X,Y)=\cfrac{2MI(X,Y)}{H(X)+H(Y)} NMI(X,Y)=H(X)+H(Y)2MI(X,Y)
其中,
H ( X ) = P A ( 0 ) log 1 P A ( 0 ) + P A ( 1 ) log 1 P A ( 1 ) H(X)=P_{A}(0)\log \frac{1}{P_{A}(0)}+P_{A}(1)\log \frac{1}{P_{A}(1)} H(X)=PA(0)logPA(0)1+PA(1)logPA(1)1
H ( Y ) = P B ( 0 ) log 1 P B ( 0 ) + P B ( 1 ) log 1 P B ( 1 ) H(Y)=P_{B}(0)\log \frac{1}{P_{B}(0)}+P_{B}(1)\log \frac{1}{P_{B}(1)} H(Y)=PB(0)logPB(0)1+PB(1)logPB(1)1
即可计算出 N M I NMI NMI 值。这样就可以用它来判断不同聚类结果与标准结果的相似程度,越接近1,表示聚类结果越好。
接下来用代码实现。同样, A A A 是经过某种算法聚类后,得到的结果; B B B 是标准的聚类结果。
import math
import numpy as np
from sklearn import metrics
def NMI(A, B):
# 样本点数
total = len(A) # 数据及的个数
A_ids = set(A) # 创建一个无序不重复的集合,保存A簇的个数
B_ids = set(B) # 保存B簇的个数
# 互信息计算
MI = 0
eps = 1.4e-45 # 防止出现log 0的情况
for idA in A_ids: # 对于A中的每一个簇
for idB in B_ids: # 对于B中的每一个簇
idAOccur = np.where(A == idA) # np.where(condition),则输出满足条件 (即非0) 元素的坐标
idBOccur = np.where(B == idB) # 一个簇的元素所对应的位置
idABOccur = np.intersect1d(idAOccur, idBOccur) # 找到A/B位置的交集
px = 1.0 * len(idAOccur[0])/total
py = 1.0 * len(idBOccur[0])/total
pxy = 1.0 * len(idABOccur)/total
MI = MI + pxy * math.log(pxy/(px * py) + eps, 2)
# 标准化互信息
Hx = 0
for idA in A_ids:
idAOccurCount = 1.0 * len(np.where(A == idA)[0])
Hx = Hx - (idAOccurCount/total)*math.log(idAOccurCount/total+eps, 2)
Hy = 0
for idB in B_ids:
idBOccurCount = 1.0 * len(np.where(B == idB)[0])
Hy = Hy - (idBOccurCount/total)*math.log(idBOccurCount/total+eps, 2)
MIhat = 2.0 * MI / (Hx + Hy)
return MIhat
if __name__ == '__main__':
A = np.array([1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3])
B = np.array([1,2,1,1,1,1,1,2,2,2,2,3,1,1,3,3,3])
print(NMI(A, B))
print(metrics.normalized_mutual_info_score(A, B)) # 直接调用函数计算的互信息
结果如下:
参考文章
聚类算法初探(七)聚类分析的效果评测
轮廓系数-百度百科
聚类性能评估-轮廓系数
sklearn之聚类评估指标—轮廓系数
信息论基础
互信息-百度百科
标准化互信息NMI计算步骤及其Python实现

