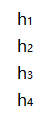GNN手写字体识别java_深度之眼Paper带读笔记GNN.09.GGNN
文章目录
前言
本课程来自深度之眼,部分截图来自课程视频。
文章标题:Gated Graph Sequence Neural
Networks
门控序列图神经网络(GGNN)
作者:Yujia Li∗& Richard Zemel
单位:Department of Computer Science, University of Toronto
发表会议及时间:ICLR2016
公式输入请参考:在线Latex公式
论文结构
Abstract:提出本文使用GRU来更新图的节点信息,在一些bAbI任务上验证了模型的有效性。
Introduction:主要贡献是对图神经网络的扩展,解决序列输出任务,提出了GGS-NNs模型。
Graph Neural Networks:回顾之前的图神经网络信息前向传播规则,表示符号。
Gated Graph Neural Networks:提出一个使用GRU更新节点信息的GGNN模型,并设计了一个简单的注意力机制的图的表征。
Gated Graph Sequence Neural Networks:提出GGS-NNs模型输出序列。
Explanatory Applications:实验探究模型有效性:bAbI任务、最短路径、欧拉圆。
Program Verification With GGSNNs:使用GGS-NNs模型实现自动化的程序验证。
Related Work:回顾了之前的LSTM、GRU等深度学习模型,DeepWalk等GNN模型。
Discussion:讨论实验的多个任务本质都是图结构,以及目前模型的局限性。
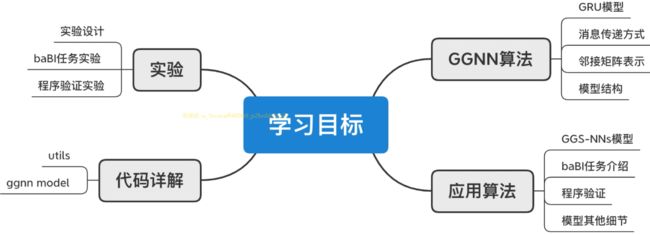
学习目标
泛读
研究背景
第一个是GNN,直接上图,具体讲解可以参考上上一篇笔记
第二个是逻辑推理任务bAbI任务简介
Some bAbl tasks [ Weston et al.,2015]. We used symbolic format of the data, so results not directly comparable with other people’s results.
下面是一个例子,如何将一个逻辑推理转换为一个图
上面是原始数据,去掉一些干扰和无用项得到下面的东西:
上图中,可以看到边有多种类型,这里要注意的是D到G是has_fear关系,如果后面还有节点,例如:G has_fear M,那么D和M不一定是has_fear关系。
下面看几个论文中逻辑推理的例子:
Task 3: Three Supporting Facts John picked up the apple.
John went to the office.
John went to the kitchen.
John dropped the apple.
Where was the apple before the kitchen? A:office
Task 4:Two Argument Relations The office is north of the bedroom.
The bedroom is north of the bathroom.
The kitchen is west of the garden.
What is north of the bedroom?A:office What is the bedroom north of?A:bathroom
Task 5:Three Argument Relations
Mary gave the cake to Fred.
Fred gave the cake to Bill.
Jeff was given the milk by Bill.
Who gave the cake to Fred?A:Mary
Who did Fred give the cake to?A:Bill
Task 6:Yes/No Questions
John moved to the playground.
Daniel went to the bathroom.
John went back to the hallway.
Is John in the playground?A:no
Is Daniel in the bathroom?A:yes
Task 15:Basic Deduction
Sheep are afraid of wolves.
Cats are afraid of dogs.
Mice are afraid of cats.
Gertrude is a sheep.
What is Gertrude afraid of?A:wolves
Task 16:Basic Induction
Lily is a swan.
Lily is white.
Bernhard is green.
Greg is a swan.
What color is Greg?A:white
Task 17:Positional Reasoning
The triangle is to the right of the blue square.
The red square is on top of the blue square.
The red sphere is to the right of the blue square.
Is the red sphere to the right of the blue square?A:yes
Is the red square to the left of the triangle?A:yes
Task 18: Size Reasoning
The football fits in the suitcase.
The suitcase fits in the cupboard.
The box is smaller than the football.
Will the box fit in the suitcase?A: yes
Will the cupboard fit in the box?A: no
Task 19: Path Finding(难)
The kitchen is north of the hallway.
The bathroom is west of the bedroom.
The den is east of the hallway.
The office is south of the bedroom.
How do you go from den to kitchen?A: west, north
How do you go from office to bathroom? A: north, west
Task 20: Agent’s Motivations John is hungry.
John goes to the kitchen.
John grabbed the apple there.
Daniel is hungry.
Where does Daniel go?A: kitchen
Why did John go to the kitchen? A: hungry
下面看一个具体例子:
Initialization
Problem specific node annotations in
h
v
(
0
)
h_v^{(0)}
hv(0)(这个可以看做之前的节点的特征X,0表示输入层)
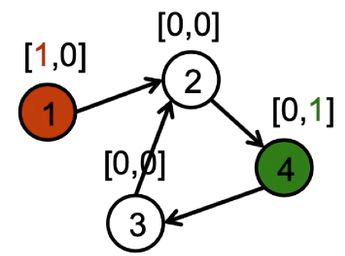
Example reachability problem:can we go from
A
{\color{Red} A}
A to
B
{\color{Green} B}
B?
It is easy to learn a propagation model that copies and adds the first bit to a node’s neighbor.(意思是将节点的二维特征
h
v
(
0
)
h_v^{(0)}
hv(0)表示中的第一维进行复制,将红色节点的1复制到与它相连的节点上)
It is easy to learn an output model that outputs yes if it sees the
[
■
,
■
]
[{\color{Red} \blacksquare},{\color{Green} \blacksquare}]
[■,■] pattern,otherwise not output yes.
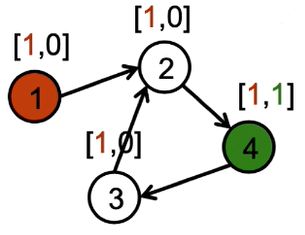
同样的,如果反过来,如下图所示,将节点4的第一维特征进行复制操作,最后节点1的特征并不是
[
■
,
■
]
[{\color{Red} \blacksquare},{\color{Green} \blacksquare}]
[■,■],因此我们可以推断,4不能到1。
将上面的例子一般化:
节点v的特征在第t个propagation step可以记为:
h
v
(
t
)
h_v^{(t)}
hv(t)
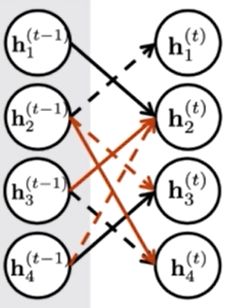
Propagate representations along edges, allow multiple edge types and propagation on both directions.
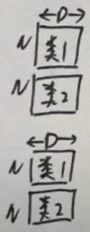
可以是有向图以及多个类型的边,例如上图中有两种类型的边(红色和黑色,实线代表入度,虚线代表出度),则特征可以表示为:
h
v
(
t
)
=
∑
v
′
∈
I
N
(
v
)
f
(
h
v
′
(
t
−
1
)
,
l
(
v
′
,
v
)
)
+
∑
v
′
∈
O
U
T
(
v
)
f
(
h
v
′
(
t
−
1
)
,
l
(
v
,
v
′
)
)
h_v^{(t)}=\sum_{v'\in IN(v)}f(h_{v'}^{(t-1)},l_{(v',v)})+\sum_{v'\in OUT(v)}f(h_{v'}^{(t-1)},l_{(v,v')})
hv(t)=v′∈IN(v)∑f(hv′(t−1),l(v′,v))+v′∈OUT(v)∑f(hv′(t−1),l(v,v′))
l
(
v
,
v
′
)
l_{(v,v')}
l(v,v′)代表Edge type and direction
t-1表示前一时刻
聚合函数可以表示为:
f
(
h
v
′
(
t
−
1
)
,
l
(
v
′
,
v
)
)
=
A
l
(
v
,
v
′
)
h
v
′
(
t
−
1
)
+
b
l
(
v
,
v
′
)
f(h_{v'}^{(t-1)},l_{(v',v)})=A^{l_{(v,v')}}h_{v'}^{(t-1)}+b^{l_{(v,v')}}
f(hv′(t−1),l(v′,v))=Al(v,v′)hv′(t−1)+bl(v,v′)
这里A这个要学习的参数对于不同类型的边是不一样的。
研究意义
·提升在图结构中的长期的信息传播
·消息传播中使用GRU,使用固定数量的步数T的递归循环得到节点表征
·边的类型、方向敏感的神经网络参数设计,类比RGCN
·多类应用问题,展示了图神经网络广阔的应用和强大的表征能力
摘要
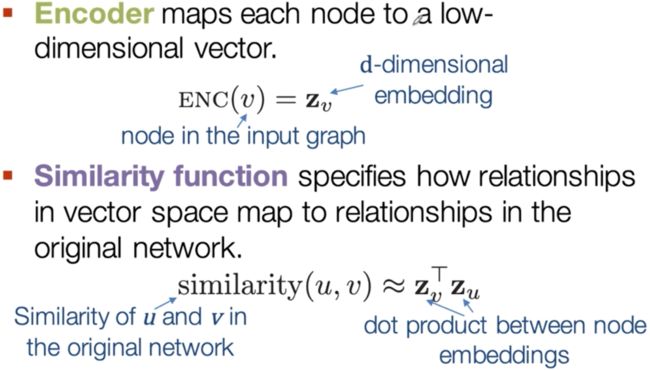
1.本文提出了一种针对图数据的特征学习技术。
In this work, we study feature learning techniques for graph-structured inputs.
2.本文使用门控循环神经网络(GRU)来学习点的特征,同时扩展模型支持序列输出。
Our starting point is previous work on Graph Neural Networks (Scarselli et al., 2009), which we modify to use gated recurrent units and modern optimization techniques and then extend to output sequences.
3.本文我们在一些简单的人工智能(bAbI)和图算法学习任务验证了模型的能力。
We demonstrate the capabilities on some simple AI (bAbI) and graph algorithm learning tasks.
4.在程序验证任务中,通过使用图数据结构来表示进一步验证了模型的能力。
We then show it achieves state-of-the-art performance on a problem from program verification, in which subgraphs need to be described as abstract data structures.
章节
Introduction
Graph Neural Networks
2.1 Propagation Model
2.2 Output Model and Learning
Gated Graph Neural Networks
3.1 Node Annotations
3.2 Propagation Model
3.3 Output Models
Gated Graph Sequence Neural Networks
Explanatory Applications
5.1 Babi Tasks
5.2 Learning Graph Algorithms
Program Verification With GGS-NNs
6.1 Formalization
6.2 Formulation As GGS-NNs
6.3 Model Setup Details
6.4 Batch Prediction Details
6.5 Experiments
Related Work
Discussion
精读
细节一:GRU模型回顾
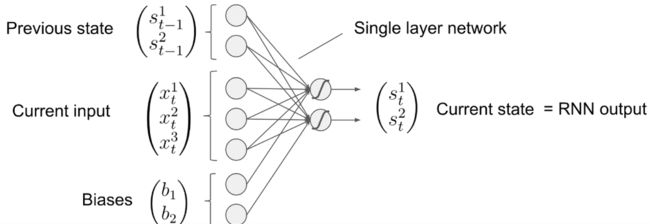
原始RNN:
最上面那里是向量对应的维度
如果每一个状态state size:n=2,输入大小input size:n=3则上面的公式可以经过以下推导得到一个DNN中某一层的形式:
s
t
=
φ
(
W
s
t
−
1
+
U
x
t
+
b
)
(
s
t
1
s
t
2
)
=
φ
(
(
w
11
w
12
w
21
w
22
)
(
s
t
−
1
1
s
t
−
1
2
)
+
(
u
11
u
12
u
13
u
21
u
22
u
23
)
(
x
t
1
x
t
2
x
t
3
)
+
(
b
1
b
2
)
)
=
φ
(
(
w
11
s
t
−
1
1
+
w
12
s
t
−
1
2
w
21
s
t
−
1
1
+
w
22
s
t
−
1
2
)
+
(
u
11
x
t
1
+
u
12
x
t
2
+
u
13
x
t
3
u
21
x
t
1
+
u
22
x
t
2
+
u
12
x
t
3
)
+
(
b
1
b
2
)
)
=
φ
(
(
w
11
s
t
−
1
1
+
w
12
s
t
−
1
2
+
u
11
x
t
1
+
u
12
x
t
2
+
u
13
x
t
3
w
21
s
t
−
1
1
+
w
22
s
t
−
1
2
+
u
21
x
t
1
+
u
22
x
t
2
+
u
12
x
t
3
)
+
(
b
1
b
2
)
)
=
φ
(
(
w
11
w
12
u
11
u
12
u
13
w
21
w
22
u
21
u
22
u
23
)
(
s
t
−
1
1
s
t
−
1
2
x
t
1
x
t
2
x
t
3
)
+
(
b
1
b
2
)
)
\begin{aligned} s_t&=\varphi(Ws_{t-1}+Ux_t+b)\\ \binom{s_t^1}{s_t^2}&=\varphi\left (\begin{pmatrix} w_{11} & w_{12}\\ w_{21} & w_{22} \end{pmatrix}\binom{s_{t-1}^1}{s_{t-1}^2} +\begin{pmatrix} u_{11} & u_{12} & u_{13}\\ u_{21} & u_{22} & u_{23} \end{pmatrix}\begin{pmatrix} x_t^1\\x_t^2\\x_t^3 \end{pmatrix}+\binom{b_1}{b_2}\right )\\ &=\varphi\left (\begin{pmatrix} w_{11}s_{t-1}^1+w_{12}s_{t-1}^2\\ w_{21}s_{t-1}^1+w_{22}s_{t-1}^2 \end{pmatrix}+\begin{pmatrix} u_{11}x_{t}^1+u_{12}x_{t}^2+u_{13}x_{t}^3\\ u_{21}x_{t}^1+u_{22}x_{t}^2+u_{12}x_{t}^3 \end{pmatrix}+\binom{b_1}{b_2}\right )\\ &=\varphi\left (\binom{w_{11}s_{t-1}^1+w_{12}s_{t-1}^2+u_{11}x_{t}^1+u_{12}x_{t}^2+u_{13}x_{t}^3}{ w_{21}s_{t-1}^1+w_{22}s_{t-1}^2+u_{21}x_{t}^1+u_{22}x_{t}^2+u_{12}x_{t}^3}+\binom{b_1}{b_2}\right )\\ &=\varphi\left (\begin{pmatrix} w_{11} & w_{12}&u_{11} & u_{12} & u_{13} \\ w_{21} & w_{22}&u_{21} & u_{22} & u_{23} \end{pmatrix}\begin{pmatrix} {s_{t-1}^1}\\{s_{t-1}^2} \\x_t^1\\x_t^2\\x_t^3 \end{pmatrix}+\binom{b_1}{b_2}\right ) \end{aligned}
st(st2st1)=φ(Wst−1+Uxt+b)=φ⎝⎛(w11w21w12w22)(st−12st−11)+(u11u21u12u22u13u23)⎝⎛xt1xt2xt3⎠⎞+(b2b1)⎠⎞=φ((w11st−11+w12st−12w21st−11+w22st−12)+(u11xt1+u12xt2+u13xt3u21xt1+u22xt2+u12xt3)+(b2b1))=φ((w21st−11+w22st−12+u21xt1+u22xt2+u12xt3w11st−11+w12st−12+u11xt1+u12xt2+u13xt3)+(b2b1))=φ⎝⎜⎜⎜⎜⎛(w11w21w12w22u11u21u12u22u13u23)⎝⎜⎜⎜⎜⎛st−11st−12xt1xt2xt3⎠⎟⎟⎟⎟⎞+(b2b1)⎠⎟⎟⎟⎟⎞
把矩阵用大写notation表示:
s
t
=
φ
(
W
c
[
s
t
−
1
,
x
t
]
+
b
)
s_t=\varphi\left (W_c[s_{t-1},x_t]+b\right )
st=φ(Wc[st−1,xt]+b)
可以把偏置也放到参数中去变成:
(
s
t
1
s
t
2
)
=
φ
(
(
w
11
w
12
u
11
u
12
u
13
b
1
w
21
w
22
u
21
u
22
u
23
b
2
)
(
s
t
−
1
1
s
t
−
1
2
x
t
1
x
t
2
x
t
3
1
)
)
s
t
=
φ
(
W
c
[
s
t
−
1
,
x
t
,
1
]
)
\begin{aligned} \binom{s_t^1}{s_t^2}&=\varphi\left (\begin{pmatrix} w_{11} & w_{12}&u_{11} & u_{12} & u_{13}& b_1\\ w_{21} & w_{22}&u_{21} & u_{22} & u_{23}&b_2 \end{pmatrix}\begin{pmatrix} {s_{t-1}^1}\\{s_{t-1}^2} \\x_t^1\\x_t^2\\x_t^3\\1 \end{pmatrix}\right )\\ s_t&=\varphi\left (W_c[s_{t-1},x_t,1]\right ) \end{aligned}
(st2st1)st=φ⎝⎜⎜⎜⎜⎜⎜⎛(w11w21w12w22u11u21u12u22u13u23b1b2)⎝⎜⎜⎜⎜⎜⎜⎛st−11st−12xt1xt2xt31⎠⎟⎟⎟⎟⎟⎟⎞⎠⎟⎟⎟⎟⎟⎟⎞=φ(Wc[st−1,xt,1])
当然,1也经常省略:
s
t
=
φ
(
W
b
[
s
t
−
1
,
x
t
]
)
s_t=\varphi\left (W_b[s_{t-1},x_t]\right )
st=φ(Wb[st−1,xt])
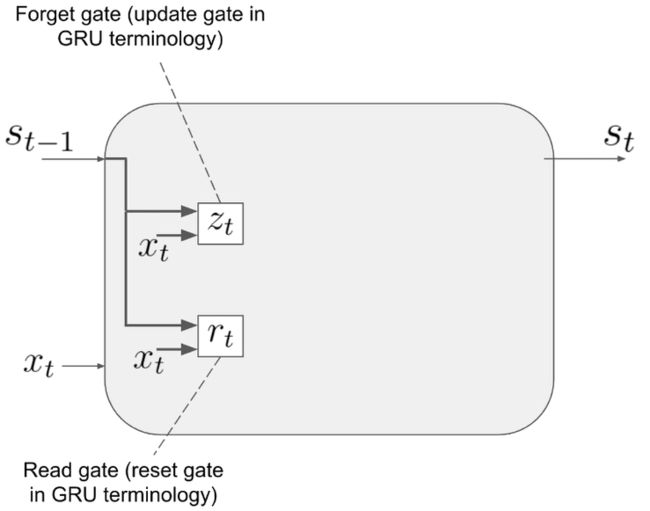
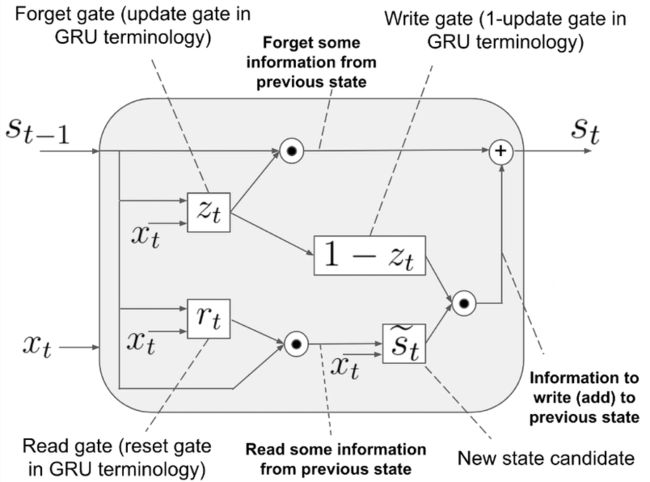
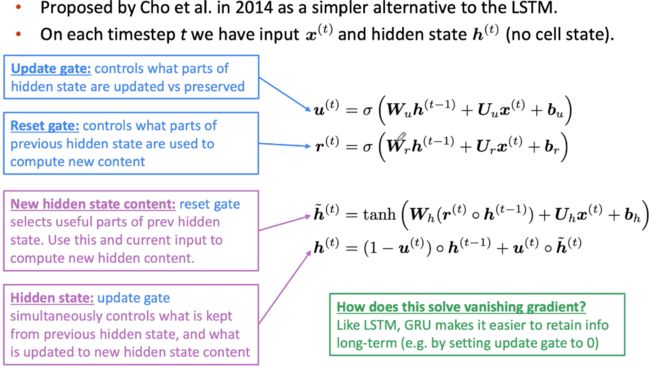
然后看看GRU,下面的描述和原文的叫法有些许出入:
这里得到更新门和重置门的公式分别为:
R
e
a
d
g
a
t
e
:
r
t
=
σ
(
W
r
s
t
−
1
+
U
r
x
t
+
b
r
)
Read~gate:r_t=\sigma(W_rs_{t-1}+U_rx_t+b_r)
Read gate:rt=σ(Wrst−1+Urxt+br)
F
o
r
g
e
t
g
a
t
e
:
z
t
=
σ
(
W
z
s
t
−
1
+
U
z
x
t
+
b
z
)
Forget~gate:z_t=\sigma(W_zs_{t-1}+U_zx_t+b_z)
Forget gate:zt=σ(Wzst−1+Uzxt+bz)
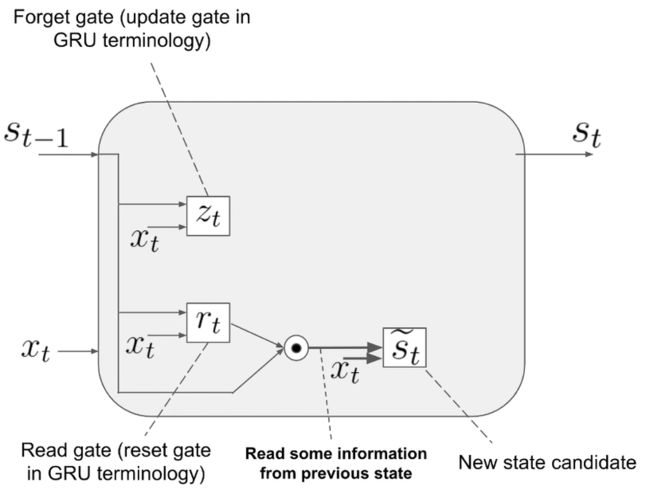
前一时刻的状态和重置门点乘,表示要遗忘或者保留多少前一时刻的内容。得到候选状态:
s
~
t
=
ϕ
(
W
(
r
t
⋅
s
t
−
1
)
+
U
x
t
+
b
)
\tilde s_t=\phi(W(r_t\cdot s_{t-1})+Ux_t+b)
s~t=ϕ(W(rt⋅st−1)+Uxt+b)
更新门也有一系列操作如下图:
最后得到当前状态的公式为::
s
t
=
z
t
⋅
s
t
−
1
+
(
1
−
z
t
)
⋅
s
~
t
s_t=z_t\cdot s_{t-1}+(1-z_t)\cdot \tilde s_t
st=zt⋅st−1+(1−zt)⋅s~t
GRU比LSTM的参数要少,门少些呗,所以效率更高一些。
细节二:GGNN模型
Propagation Model
GNN propagation model with gating and other minor differences.
邻居信息的汇聚:
a
(
t
)
=
A
h
(
t
−
1
)
+
b
a^{(t)}=Ah^{(t-1)}+b
a(t)=Ah(t−1)+b
上式中如果h没有下标v则表示所有点的隐藏层状态的堆叠成的列向量
如果每个点的隐藏层状态都是D维的,有N个点的话,那么堆叠后的
h
t
−
1
h^{t-1}
ht−1就是N×D×1维的(1代表是列向量,N代表从上到下有N个隐藏层状态,D代表每个状态有D维)。右边则有:
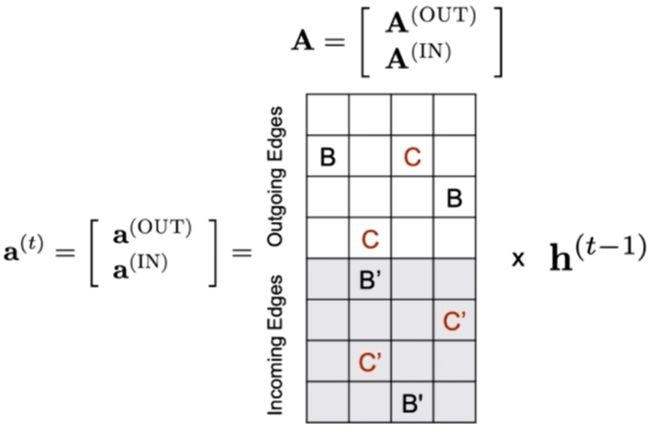
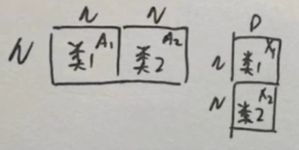
上图中把A做了一个转置,原来的邻接矩阵是N×N的,分别考虑出入度后,现在变成了N×2N的了每个参数又是D维的(要和h的D维要对上不然矩阵没法计算),A这个大矩阵维度就是ND×2ND的,如果单求某个点的汇聚信息,例如
a
2
a_2
a2的时候,就是从A这个大矩阵取2号节点对应的两行,然后堆起来,维度就变成2×N的,加上每个参数的维度变成:2D×ND
B
空
格
C
空
格
空
格
空
格
空
格
C
′
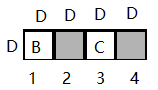
\begin{aligned} &B&空格 &~~C & 空格\\ &空格 &空格 &~~空格& C' \end{aligned}
B空格空格空格 C 空格空格C′
GRU结合GNN:
Reset gate
r
v
t
=
σ
(
W
r
a
v
(
t
)
+
U
r
h
v
(
t
−
1
)
)
r_v^t=\sigma\left (W^ra_v^{(t)}+U^rh_v^{(t-1)}\right )
rvt=σ(Wrav(t)+Urhv(t−1))
Update gate
z
v
t
=
σ
(
W
z
a
v
(
t
)
+
U
z
h
v
(
t
−
1
)
)
z_v^t=\sigma\left (W^za_v^{(t)}+U^zh_v^{(t-1)}\right )
zvt=σ(Wzav(t)+Uzhv(t−1))
h
v
(
t
)
~
=
tanh
(
W
a
v
(
t
)
+
U
(
r
v
t
⊙
h
v
(
t
−
1
)
)
)
\widetilde {h_v^{(t)}} = \tanh \left (Wa_v^{(t)}+U(r_v^t\odot h_v^{(t-1)})\right )
hv(t)
=tanh(Wav(t)+U(rvt⊙hv(t−1)))
h
v
(
t
)
=
(
1
−
z
v
t
)
⊙
h
v
(
t
−
1
)
+
z
v
t
⊙
h
v
(
t
)
h_v^{(t)}= (1-z_v^t)\odot h_v^{(t-1)}+z_v^t\odot h_v^{(t)}
hv(t)=(1−zvt)⊙hv(t−1)+zvt⊙hv(t)
output model
单步输出:
对每个节点的输入
x
v
x_v
xv,经过T个时间步后,经过GGNN模型g,得到一个分数:
o
v
=
g
(
h
v
(
T
)
,
x
v
)
o_v=g(h_v^{(T)},x_v)
ov=g(hv(T),xv)
然后将所有节点的分数经过softmax,得到每一个点对应的权重
对于整个图的表示输出:
h
g
=
tanh
(
∑
v
∈
V
σ
(
i
(
h
v
(
T
)
,
x
v
)
)
⊙
tanh
(
j
(
h
v
(
T
)
,
x
v
)
)
)
h_g=\tanh(\sum_{v\in V}\sigma(i(h_v^{(T)},x_v))\odot\tanh(j(h_v^{(T)},x_v)))
hg=tanh(v∈V∑σ(i(hv(T),xv))⊙tanh(j(hv(T),xv)))
i and j are feed-forward networks.
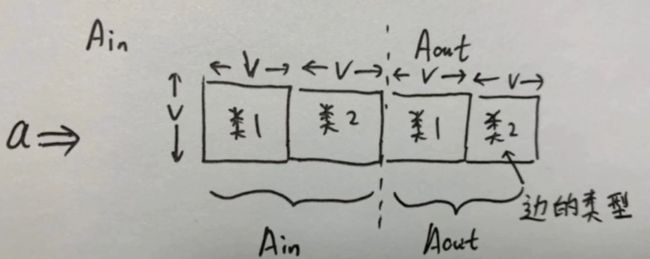
模型框架
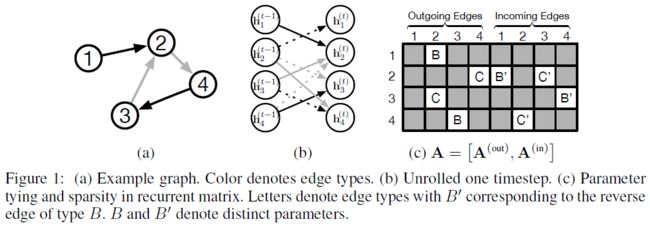
论文的图1:
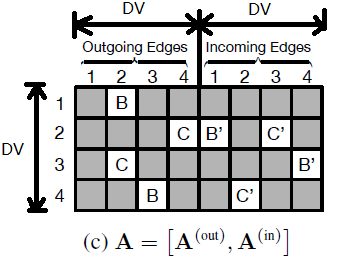
从图a中可以看到有两种边(灰色和黑色),将其展开得到图b,实线代表入度邻居,虚线代表出度邻居。颜色和线的类型在图c中分别用B/C/B’/C’表示。
GGNN模型特点
Replaces propagation model with GRU.
Unrolls recurrence for T time-steps(instead of till convergence).
Uses Backprop-through-time to compute gradients.
细节三:GGS-NNs模型
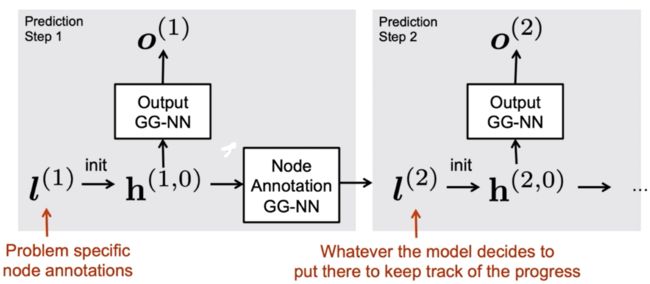
用来做序列的输出,每一个时间步都从所有节点里面挑一个作为当前时间步输出
· GGS-NN: Several GG-NNs operate in sequence to produce outputs
o
(
1
)
,
o
(
2
)
,
⋯
o
(
K
)
o^{(1)},o^{(2)},\cdots o^{(K)}
o(1),o(2),⋯o(K).
·
X
(
k
)
=
[
x
1
(
k
)
;
x
2
(
k
)
⋯
x
∣
V
∣
(
k
)
]
X^{(k)}=[ x_1^{(k)};x_2^{(k)}\cdots x_{|V|}^{(k)}]
X(k)=[x1(k);x2(k)⋯x∣V∣(k)] is matrix of node annotations.
这里annotations相当于GCN里面点的feature,但是这里具体是和前面研究背景中具体例子中提到的每个点有个0-1的特征表示,用来推断是否两个点能连通。
· May be initialized with 1-0 values, but in general are real valued.
· 2个GG-NNs的参数:
·
F
o
F_o
Fo-to predict
o
(
K
)
o^{(K)}
o(K) from
X
(
k
)
X^{(k)}
X(k).对应下图的Output框框
·
F
x
F_x
Fx-to predict
X
(
k
+
1
)
X^{(k+1)}
X(k+1) from
X
(
k
)
X^{(k)}
X(k).对应下图Annotation框框
下图中的l变成h要经过padding。
下面是原文的图文
·
H
(
k
,
t
)
=
[
h
1
(
k
,
t
)
,
h
2
(
k
,
t
)
.
.
.
h
∣
V
∣
(
k
,
t
)
]
H^{(k,t)}=[h_1^{(k,t)},h_2^{(k,t)}... h_{|V|}^{(k,t)}]
H(k,t)=[h1(k,t),h2(k,t)...h∣V∣(k,t)]are node representations.
·$H^{(k,1) $ set by concatenating 0 to
X
(
k
)
X^{(k)}
X(k).(这里是padding补0操作)
·
F
o
F_o
Fo and
F
x
F_x
Fx can have shared propagation models with separate outputs, or have separate propagation models.
Two training settings:
· Providing only final supervised node annotation.利用最终的label直接end2end训练
· Providing intermediate node annotations as supervision-也可以用中间结果加上label进行训练(可能需要人为标注,没有中间的label那么中间结果
X
(
k
)
X^{(k)}
X(k)可以直接看做隐藏层状态)
· · Decouples the sequential learning process (BPTT) into independent time steps.
· · Condition the further predictions on the previous predictions.
细节四:bAbI任务
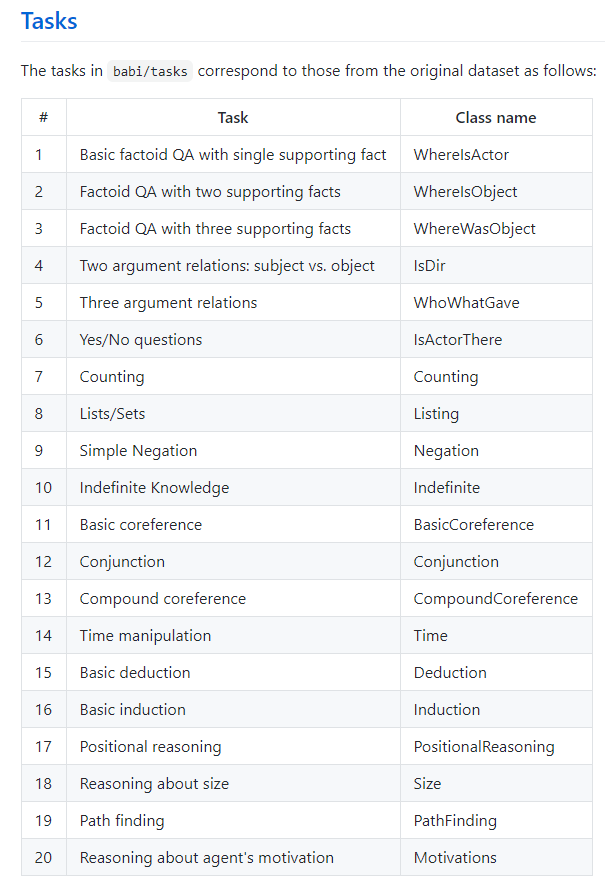
简介
·20 tasks to test forms of reasoning like counting/path-finding/deduction.
· Requires symbolic form to get “stories”-Sequences of relations between entities, then convert them to a graph.
· Each entity is a node, each relation is an edge.
· The full story is a graph.
· Questions are denoted as “eval”.
实验方法
We tried GG-NNs on bAbl task 4,15,16(all three are node-selection),18(graph-level classification) and this model is able to solve all of them to 100% accuracy with only 50 training examples and less than 600 model parameters.
然后以RNN和LSTM做baseline进行对比
RNN/LSTM trained on token streams
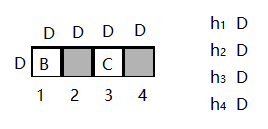
输入:
<
D
>
<
i
s
>
<
A
>
<
∖
n
>
<
B
>
.
.
…
..…
..…
<
B
>
<
h
a
s
_
f
e
a
r
>
输出:
<
A
>
参数情况:
# parameters: RNN 5k, LSTM 30k
950 training,50 validation (1000 trainval)
1000 test examples
Start with using only 50 training examples, then keep using more until test accuracy reaches 95%
or above.(论文还做了一个实验,将训练样本从50个慢慢增加,直到准确率到达95%)
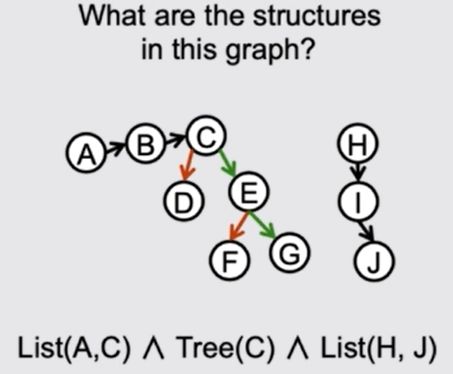
还对论文中提到的输出节点序列的GGS-NNs模型做了实验,主要是两类,一个是最短路径预测,一个是对图中的结构进行判别。
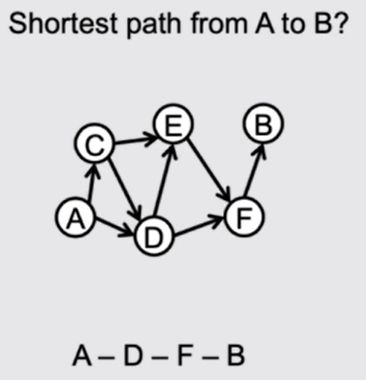
论文中还用GGS-NNs来解了bAbI的19号任务,做路径查找,每次输出一个节点作为路径:
bAbl task 19(path finding): find the path from one node to another on a graph, guarantee there’s only one path.
We created two bAbl-like but more challenging tasks:
Shortest path: find the shortest among possibly multiple paths between two nodes on a graph.
Eulerian circuit: 欧拉回路检测 find the Eulerian circuit of a 2-regular connected graph (a graph which is a cycle),a distractor graph is added to make it more challenging.
注:具体将句子转化为图的步骤或方法看研究背景。
细节五:RNN和LSTM分析
附录B
1.图结构数据,GNN模型更适用
2.RNN长记忆能力差,LSTM有改善但并不能完全解决
3.图结构的数据数据顺序不影响输出,不存在RNN等建模的序列化信息
原文有这么一个例子:
3 connected-to 7
7 connected-to 3
1 connected-to 2
2 connected-to 1
5 connected-to 7
7 connected-to 5
0 connected-to 4
4 connected-to 0
1 connected-to 0
0 connected-to 1
8 connected-to 6
6 connected-to 8
3 connected-to 6
6 connected-to 3
5 connected-to 8
8 connected-to 5
4 connected-to 2
2 connected-to 4
eval eulerian-circuit 5 7 5,7,3,6,8
上面实际上描述了两个欧拉圆:This describes a graph with two cycles 3-7-5-8-6 and 1-2-4-0
第一条边在第一行就有描述,3和7,RNN或者LSTM很难记住最开始的信息。下面是RNN的输入序列。
n4 e1 n8 eol n8 e1 n4 eol n2 e1 n3 eol n3 e1 n2 eol n6 e1 n8 eol
n8 e1 n6 eol n1 e1 n5 eol n5 e1 n1 eol n2 e1 n1 eol n1 e1 n2 eol
n9 e1 n7 eol n7 e1 n9 eol n4 e1 n7 eol n7 e1 n4 eol n6 e1 n9 eol
n9 e1 n6 eol n5 e1 n3 eol n3 e1 n5 eol q1 n6 n8 ans 6 8 4 7 9
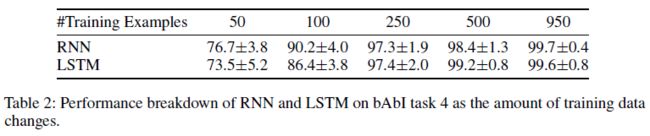
实验结果及分析
bAbI任务
括号里面是训练使用的sample数量
不同训练集大小的结果:
其他任务(主要是针对GGS-NNs的)
总结
关键点
·GGNN模型结构
·参数矩阵由边的类型和方向决定
·bAbI数据图结构
创新点
·GRU更新消息框架
·序列模型GGS-NNs
·多个新应用
启发点
·用RNN的方法来定义GNN
·迭代不要求收敛,可迭代固定步长T,注意初始化(node annotations)
·GGNN的graph layer层数可以较高
·每一种边对应一个参数矩阵,可以处理异构图
·与GNN常用框架之间的联系
·将CNN和RNN发展的技术应用到GNN
复现
·python 3.7.6
·torch 1.3.1
·numpy 1.18.1
https://github.com/chingyaoc/ggnn.pytorch
数据集
https://github.com/chingyaoc/ggnn.pytorch/tree/master/babi_data
图数据基本是在graphs文件中:
1 1 2(点空格边空格点)
3 1 1(点空格边空格点)
? 1 1 2(eval的数据,以问号开头然后接:?空格边空格点空格点)
文件前面的数字对应的是bAbI任务序号
数据集原始链接,内含介绍
github.com/facebookarchive/bAbI-tasks
main.py
主函数入口
import argparse
import random
import torch
import torch.nn as nn
import torch.optim as optim
from model import GGNN
from utils.train import train
from utils.test import test
from utils.data.dataset import bAbIDataset
from utils.data.dataloader import bAbIDataloader
parser = argparse.ArgumentParser()
parser.add_argument('--task_id', type=int, default=4, help='bAbI task id')#bAbI任务序号,根据这个来选择要做哪个任务
parser.add_argument('--question_id', type=int, default=0, help='question types')#bAbI问题序号,每个类型的问题都训练了单独的GGNN模型
parser.add_argument('--workers', type=int, help='number of data loading workers', default=2)#多线程
parser.add_argument('--batchSize', type=int, default=10, help='input batch size')#batch大小
parser.add_argument('--state_dim', type=int, default=4, help='GGNN hidden state size')#h_v维度,这个大小很重要,默认是4,后面代码中大量用到这个数字
parser.add_argument('--n_steps', type=int, default=5, help='propogation steps number of GGNN')#GGNN层数,默认是5层
parser.add_argument('--niter', type=int, default=10, help='number of epochs to train for')#epoch数量
parser.add_argument('--lr', type=float, default=0.01, help='learning rate')#学习率
parser.add_argument('--cuda', action='store_true', help='enables cuda')#是否使用GPU
parser.add_argument('--verbal', action='store_true', help='print training info or not')#是否大于中间训练结果
parser.add_argument('--manualSeed', type=int, help='manual seed')#随机数种子大小
#opt=parser.parse_args(args=[])#jupyter里面用这个才行
opt = parser.parse_args()
print(opt)#打印参数
if opt.manualSeed is None:
opt.manualSeed = random.randint(1, 10000)
print("Random Seed: ", opt.manualSeed)
random.seed(opt.manualSeed)
torch.manual_seed(opt.manualSeed)
opt.dataroot = 'babi_data/processed_1/train/%d_graphs.txt' % opt.task_id#数据集路径,这里根据任务序号选定要训练哪个任务
if opt.cuda:
torch.cuda.manual_seed_all(opt.manualSeed)
def main(opt):
#读入训练集
#dataroot:数据集路径,question id:bAbI问题序号,is train:True
train_dataset = bAbIDataset(opt.dataroot, opt.question_id, True)
#封装成DataLoader
train_dataloader = bAbIDataloader(train_dataset, batch_size=opt.batchSize, \
shuffle=True, num_workers=2)
#读入测试集
test_dataset = bAbIDataset(opt.dataroot, opt.question_id, False)
test_dataloader = bAbIDataloader(test_dataset, batch_size=opt.batchSize, \
shuffle=False, num_workers=2)
opt.annotation_dim = 1 # for bAbI,annotation只要1维就ok
opt.n_edge_types = train_dataset.n_edge_types#边类型数量
opt.n_node = train_dataset.n_node#最大点ID
#按opt中的参数初始化模型
net = GGNN(opt)
#将parameters等转换成double
net.double()
print(net)
#CrossEntropy作为损失函数
criterion = nn.CrossEntropyLoss()
if opt.cuda:
net.cuda()
criterion.cuda()
#adam优化器和学习率设置
optimizer = optim.Adam(net.parameters(), lr=opt.lr)
for epoch in range(0, opt.niter):
train(epoch, train_dataloader, net, criterion, optimizer, opt)
test(test_dataloader, net, criterion, optimizer, opt)
if __name__ == "__main__":
main(opt)
model.py
import torch
import torch.nn as nn
class AttrProxy(object):
"""
Translates index lookups into attribute lookups.
To implement some trick which able to use list of nn.Module in a nn.Module
see https://discuss.pytorch.org/t/list-of-nn-module-in-a-nn-module/219/2
"""
def __init__(self, module, prefix):
self.module = module
self.prefix = prefix
def __getitem__(self, i):
return getattr(self.module, self.prefix + str(i))
class Propogator(nn.Module):
"""
Gated Propogator for GGNN
Using LSTM gating mechanism
"""
def __init__(self, state_dim, n_node, n_edge_types):
super(Propogator, self).__init__()
self.n_node = n_node#最大点id
self.n_edge_types = n_edge_types#最大边id
#reset_gate
self.reset_gate = nn.Sequential(
#state_dim*3,原文公式4中可以按算法细节一中推导的写法,把h_v和a_v进行concat拼接,W和U进行拼接
#他们两个一个是D维,一个是2D维,所以就要3D维
nn.Linear(state_dim*3, state_dim),
nn.Sigmoid()
)
#update_gate,原文公式3
self.update_gate = nn.Sequential(
nn.Linear(state_dim*3, state_dim),
nn.Sigmoid()
)
#计算\tilde h^t,对应原文公式5
self.tansform = nn.Sequential(
nn.Linear(state_dim*3, state_dim),
nn.Tanh()
)
#state_cur是当前点的embedding矩阵
def forward(self, state_in, state_out, state_cur, A):
#三个维度,分别表示的是batch,点的数量N,横向的是A_in//Aout
#A的形状可以参考dataset.py的图示,左半边是Ain,右半边是Aout
A_in = A[:, :, :self.n_node*self.n_edge_types]
A_out = A[:, :, self.n_node*self.n_edge_types:]
#BMM乘法,里面三个维度,第一个维度是batch,不用关心,后面两个维度进行操作
#后两个维度:[N,(N*n_edge_types)]*[(N*n_edge_types),D]
#最后得到的a_in:[N,D],即邻居消息embedding的求和
#这里根据note2和note3,可以画出note4
a_in = torch.bmm(A_in, state_in)
a_out = torch.bmm(A_out, state_out)
#a=a_in||a_out||h_v 这里是在2号维度进行拼接,这里拼成3D维的,原因和reset gate的3D维度原因一致
#这里论文中的a_v=a_in||a_out
a = torch.cat((a_in, a_out, state_cur), 2)
#reset门
r = self.reset_gate(a)
#更新门
z = self.update_gate(a)
#原文公式5:a_v=a_in||a_out,r_v* h_v^(t-1)=r* state_cur
joined_input = torch.cat((a_in, a_out, r * state_cur), 2)
#公式6
h_hat = self.tansform(joined_input)
output = (1 - z) * state_cur + z * h_hat
return output
class GGNN(nn.Module):
"""
Gated Graph Sequence Neural Networks (GGNN)
Mode: SelectNode
Implementation based on https://arxiv.org/abs/1511.05493
"""
def __init__(self, opt):
super(GGNN, self).__init__()
#要求h_v继度大于node annotations
assert (opt.state_dim >= opt.annotation_dim, \
'state_dim must be no less than annotation_dim')
#h_v维度(4)
self.state_dim = opt.state_dim
#node annotation维度(1)
self.annotation_dim = opt.annotation_dim
#最大边id
self.n_edge_types = opt.n_edge_types
#最大点id
self.n_node = opt.n_node
#GNN层数,对应论文的T
self.n_steps = opt.n_steps
#每种边的类型+方向(in/out)独立
for i in range(self.n_edge_types):
# incoming and outgoing edge embedding
#论文中邻接矩阵A中的每一个cel1:B,B',C,C'
#每个参数矩阵都是方阵,这里是4*4的
in_fc = nn.Linear(self.state_dim, self.state_dim)
out_fc = nn.Linear(self.state_dim, self.state_dim)
#对每个模块进行命名
self.add_module("in_{}".format(i), in_fc)
self.add_module("out_{}".format(i), out_fc)
#以上内容可以看打印出来的结构图的前面四行,这里有两个类型的边,每个类型的边又分IN/OUT
self.in_fcs = AttrProxy(self, "in_")
self.out_fcs = AttrProxy(self, "out_")
#GGNN模型:Propogation Model+Output Model
# Propogation Model,GRU消息传递模型
self.propogator = Propogator(self.state_dim, self.n_node, self.n_edge_types)
# Output Model输出模型,将h_v与x_v(未padding的)做拼接输入神经网络
self.out = nn.Sequential(
#维度是[h_v^T,x_v],实际是4+1=5
nn.Linear(self.state_dim + self.annotation_dim, self.state_dim),
nn.Tanh(),
nn.Linear(self.state_dim, 1)#最后经过FC得到一维的输出,为后面做softmax(attention)做准备
)
# 以上结构,在实例运行过程中产生的网络结构打印出来的截图见下面note1
self._initialization()
def _initialization(self):
for m in self.modules():
if isinstance(m, nn.Linear):
m.weight.data.normal_(0.0, 0.02)
m.bias.data.fill_(0)
'''
前向传播函数
:param prop_state:按batch训练,维度N*D(这里忽略了batch的维度,本来batch是BATCH*N*D的大小,这里是10*4*4的大小。这里为了方便理解先按batchsize=1来理解)
:param annotation:node annotation x_v(未padding的)原始点的标注
:param A:邻接矩阵
:return:
可以参考train.py 中调用GGNN的这行代码:output = net(init_input, annotation, adj_matrix)
'''
def forward(self, prop_state, annotation, A):
for i_step in range(self.n_steps):#根据T来进行循环,这里是4
in_states = []
out_states = []
for i in range(self.n_edge_types):
# self.in_fcs[i]和self.out_fcs[i]都是D*D的方阵,这个在 __init__就初始化了 #prop_state记为P,维度是N*D,每一个行都是每个点的embedding,如果是输入第一层的h^0,那么这个玩意是原始annotationpadding出来的。
# 这里两个相乘相当于经过一个FC层
# 这一步对应下面的note2
in_states.append(self.in_fcs[i](prop_state))
out_states.append(self.out_fcs[i](prop_state))
#https://zhuanlan.zhihu.com/p/64551412(解释contiguous)
#做拼接
in_states = torch.stack(in_states).transpose(0, 1).contiguous()
#-1是bacth的数量,self.n_node*self.n_edge_types表示N*边的类型数量,state dim为论文中的h_v的embedding维度为D
#具体看note3
in_states = in_states.view(-1, self.n_node*self.n_edge_types, self.state_dim)
out_states = torch.stack(out_states).transpose(0, 1).contiguous()
out_states = out_states.view(-1, self.n_node*self.n_edge_types, self.state_dim)
#用GRU的方式消息传递,这星理解算邻居消息(论文中的a_v,公式2)
#实际上和RGCN非常相似:a_v=sum_{forall j\in N(i)对i的所有邻居}W(e)h_j,就是邻居embedding的相加
#这里面的W(e)神经网络参数是和“边的类型+边的方向”有关的
prop_state = self.propogator(in_states, out_states, prop_state, A)
#将经过T个step的prop_state,也就是h^T和annotation拼接起来送入output模型
join_state = torch.cat((prop_state, annotation), 2)
output = self.out(join_state)
#再把output结果进行求和,准备softmax
output = output.sum(2)
return output
note1
note2
记prop_state 为P(维度为N×D)也就是有N行,每行对应的是点的隐藏层embedding
进入第一层的prop_state可以看train.py,里面将annotation进行padding补0到
h
v
h_v
hv的维度一样后,作为prop_state,也就是
h
0
h_0
h0
(
←
h
v
1
→
⋮
←
h
v
n
→
)
\begin{pmatrix} \leftarrow h_{v1}\rightarrow \\ \vdots \\\leftarrow h_{vn}\rightarrow \end{pmatrix}
⎝⎜⎛←hv1→⋮←hvn→⎠⎟⎞
然后是self.in_fcs[i]和self.out_fcs[i],这里每个_fcs都是D×D维的矩阵,然后由于有两个类型的边(用原文的例子就是B和C两种类型),因此共有4个_fcs矩阵(之前提到过,每个类型的边对应的训练参数矩阵不一样是):
类1类2inBC
outB’C’
代码中
in_states.append(self.in_fcs[i](prop_state))
out_states.append(self.out_fcs[i](prop_state))
就是分别把4个_fcs与prop_state 进行矩阵相乘,然后分别append到in_states和out_states里面,
in_states里面有:
PB和PC
out_states里面有:
PB’和PC’
可以看到N×D维和D×D维的矩阵相乘后得到结果是N×D维的。
从理论上理解就可以看做是FC的WX,W就是参数(BCB’C’),X就是输入
note3
in_states = torch.stack(in_states).transpose(0, 1).contiguous()
out_states = torch.stack(out_states).transpose(0, 1).contiguous()
接着上面的note2,这里把in_states和out_state做拼接,由于每个in和out对应2个类,因此拼接后
in_states和out_state的维度变成了N×2D,具体长相为:
i
n
_
s
t
a
t
e
s
=
(
[
P
B
,
P
C
]
)
in\_states=\begin{pmatrix} [PB,PC ] \end{pmatrix}
in_states=([PB,PC])
o
u
t
_
s
t
a
t
e
=
(
[
P
B
′
,
P
C
′
]
)
out\_state=\begin{pmatrix} [PB',PC' ] \end{pmatrix}
out_state=([PB′,PC′])
然后经过
in_states = in_states.view(-1, self.n_node*self.n_edge_types, self.state_dim)
out_states = out_states.view(-1, self.n_node*self.n_edge_types, self.state_dim)
变成2N×D维度的了(如果边有三个类别就应该是3N×D)。
note4
a_in = torch.bmm(A_in, state_in)
这句代码中的A_in是从邻接矩阵A(形状看dataset.py的图示)中切出来的左半边维度是:N×(N×边类型数量)
state_in实际上是note3中的in_states ,维度是:N×边类型数量)×D
以上描述都忽略了batchsize那个维度,BMM只做上面提到的两个维度,上面两个玩意做BMM后维度就变成:N×D,用图画出来就是:
这里老师将A_in和state_in按边的类型划分块
[
A
1
;
A
2
]
[A_1;A_2]
[A1;A2]和
[
X
1
;
X
2
]
[X_1;X_2]
[X1;X2],把每个块看做矩阵的一个元素,两个分块矩阵相乘变成:
A
1
X
1
+
A
2
X
2
(1)
A_1X_1+A_2X_2\tag1
A1X1+A2X2(1)
可以看到
A
1
和
A
2
A_1和A_2
A1和A2都是N×N的邻接矩阵,X则是从最开始的
h
0
h_0
h0经过线性变换的embedding(
X
1
=
P
B
,
X
2
=
P
C
X_1=PB,X_2=PC
X1=PB,X2=PC)
公式1实际上可以看做是GCN,如果我们看其中某个点v,就是求该点所有邻居embedding信息的聚合
(
A
1
X
1
+
A
2
X
2
)
v
→
a
v
i
n
=
∑
j
∈
类
型
1
h
j
′
+
∑
j
∈
类
型
2
h
j
′
=
∑
j
∈
N
(
e
)
W
(
e
)
h
j
(2)
(A_1X_1+A_2X_2)_v\rightarrow a_{vin}=\sum_{j\in 类型1}h_j'+\sum_{j\in 类型2}h_j'=\sum_{j\in N_{(e)}}W_{(e)}h_j\tag2
(A1X1+A2X2)v→avin=j∈类型1∑hj′+j∈类型2∑hj′=j∈N(e)∑W(e)hj(2)
W
(
e
)
W_{(e)}
W(e)是不同边的对应的参数
现在稍微证明一下这个公式2和论文里面的公式2为什么是等价的。
原文的邻接矩阵和代码的邻接矩阵表示得不太一样,它把所有不同类型的边都放在一起了
其维度在之前有讲过,V代表点的个数,D是每个点的隐藏状态embedding的维度,如果把
A
(
o
u
t
)
A^{(out)}
A(out)的第2列取出来,放平就变成了:
当然,如果有V个点,最下面就是1到V,每个点还是D维,上图对应原文公式2的
A
v
:
⊤
A_{v:}^\top
Av:⊤
原文的公式2为:
a
v
(
t
)
=
A
v
:
⊤
[
h
1
(
t
−
1
)
⊤
⋯
h
∣
V
∣
(
t
−
1
)
⊤
]
⊤
+
b
a_v^{(t)}=A_{v:}^\top[h_1^{(t-1)\top}\cdots h_{|V|}^{(t-1)\top}]^\top+b
av(t)=Av:⊤[h1(t−1)⊤⋯h∣V∣(t−1)⊤]⊤+b
也就是还要去乘上
[
h
1
(
t
−
1
)
⊤
⋯
h
∣
V
∣
(
t
−
1
)
⊤
]
[h_1^{(t-1)\top}\cdots h_{|V|}^{(t-1)\top}]
[h1(t−1)⊤⋯h∣V∣(t−1)⊤],这个玩意是D维的embedding(这个玩意转置后要竖起来维度是(D×V)×D),也可以切成以V个D维小块,这里是:
原文公式2如果求上图的结果为(左边没字母的地方是0,相乘结果也是0,可以省略):
a
2
o
u
t
=
B
h
2
+
C
h
3
a_{2out}=Bh_2+Ch_3
a2out=Bh2+Ch3
归纳一下,一般化后写成:
a
v
i
n
=
∑
j
∈
N
(
e
)
W
(
e
)
h
j
a_{vin}=\sum_{j\in N_{(e)}}W_{(e)}h_j
avin=j∈N(e)∑W(e)hj
代码和公式一一对应了。
dataset.py
import numpy as np
def load_graphs_from_file(file_name):
"""
按每一组读图
图的每一行是(node1,edge,node2)
evaluation的每一行是(?,edge,node1,node2)
:param file_name:
:return:
"""
data_list = []
edge_list = []
target_list = []
with open(file_name,'r') as f:
for line in f:
#处理完一组数据后开始处理新的一组数据
if len(line.strip()) == 0:#这里判断是空行,如果有空行说明刚才读完了一组数据,下面要把这些数据丢到data_list中
#将目前读完这组数据放入data list
#data list[0]是edge list,data list[1]是target list
data_list.append([edge_list,target_list])
#清空edge_list和target_list
edge_list = []
target_list = []
else:#如果是非空行,则是同一组数据
digits = []
line_tokens = line.split(" ")#按空格切分每行数据
if line_tokens[0] == "?":#如果第一个字符是问号,代表该行数据是eval数据,忽略问号从1开始读
for i in range(1, len(line_tokens)):
digits.append(int(line_tokens[i]))
target_list.append(digits)#得到问题列表
else:#非eval数据从头开始读图
for i in range(len(line_tokens)):
digits.append(int(line_tokens[i]))
edge_list.append(digits)#得到图的边列表
return data_list
def find_max_edge_id(data_list):
max_edge_id = 0
for data in data_list:#data_list[0]是edge_list,data_list[1]是target_list
edges = data[0]
for item in edges:
if item[1] > max_edge_id:#点边点,所以1是边
max_edge_id = item[1]
return max_edge_id
def find_max_node_id(data_list):
max_node_id = 0
for data in data_list:
edges = data[0]
for item in edges:
if item[0] > max_node_id:#点边点,所以0和2是点
max_node_id = item[0]
if item[2] > max_node_id:
max_node_id = item[2]
return max_node_id
def find_max_task_id(data_list):
max_edge_id = 0
for data in data_list:
targe = data[1]#data_list[1]是target_list(三元组,边点点)
for item in targe:
if item[0] > max_edge_id:#eval行中是:边点点,这里要求最大任务边,所以是0
max_edge_id = item[0]
return max_edge_id
def split_set(data_list):
n_examples = len(data_list)
idx = range(n_examples)
train = idx[:50]#论文中用的前50个sample来训练就可以拿100%的准确率
val = idx[-50:]#后50做validation
return np.array(data_list)[train],np.array(data_list)[val]
'''
按每一种边的类型(n_tasks)分别训练一个模型
数据预处理将data_1ist按照边的类型分组得到task_data_list
:param data_list:
:param n_annotation_dim:
:return:
'''
def data_convert(data_list, n_annotation_dim):
n_nodes = find_max_node_id(data_list)
n_tasks = find_max_task_id(data_list)
task_data_list = []
#得到的最大任务边类型数量就是任务类型数量
for i in range(n_tasks):
task_data_list.append([])
for item in data_list:
#边的类型
edge_list = item[0]
target_list = item[1]
for target in target_list:#target_list(三元组:边点点)
#0代表边的类型
task_type = target[0]
#-1是最后target_list的一个,是目标输出
task_output = target[-1]
#初始化annotation,如果有n个点,其是维度为n*1的向量,初始化所有位置都设置为0,n_annotation_dim=1
annotation = np.zeros([n_nodes, n_annotation_dim])
#将target_list(三元组:边点点)中的第一个点(target[1])设置为1(np是从0开始,所以这里target[1]-1),其他位置还是0
annotation[target[1]-1][0] = 1
#根据任务边(或者说根据任务类型)添加该任务对应的边,annotation,output
task_data_list[task_type-1].append([edge_list, annotation, task_output])
return task_data_list
def create_adjacency_matrix(edges, n_nodes, n_edge_types):
#邻接矩阵A=[A_in;A_out];A_in里面有多个类型,因此其维度为:
#n_nodes*n_edge_types*2:点数*边的类型*2(in/out边的两个方向)
#通俗的说就是这个矩阵a分两大块,分别对应出度和入度
#然后出度和入度中又按照边的类型不同,每个类型又对应一个n*n的邻接矩阵拼起来。
#所以整个矩阵a的维度是:节点数量*(节点数量*边类型数量*2)
#具体看图
a = np.zeros([n_nodes, n_nodes * n_edge_types * 2])
for edge in edges:
#以edge =[a e b]为例,表示从a->b的边的类型为e
#点a
src_idx = edge[0]
#边e
e_type = edge[1]
#点b
tgt_idx = edge[2]
#(e_type-1)*n_nodes定位A_in中的e_type这个类型
a[tgt_idx-1][(e_type - 1) * n_nodes + src_idx - 1] = 1
#(e_type-1+n_edge_types)*n_nodes分开
# n_edge_types*n nodes跳过整个A_in
#(e_type-1)*n_nodes定位A_out中的e_type这个类型
a[src_idx-1][(e_type - 1 + n_edge_types) * n_nodes + tgt_idx - 1] = 1
return a
class bAbIDataset():
"""
Load bAbI tasks for GGNN
"""
def __init__(self, path, task_id, is_train):
#读图
all_data = load_graphs_from_file(path)
#最大边id
self.n_edge_types = find_max_edge_id(all_data)
#最大任务边id(evaluation中)
self.n_tasks = find_max_task_id(all_data)
#最大点id
self.n_node = find_max_node_id(all_data)
#分成train和validation
all_task_train_data, all_task_val_data = split_set(all_data)
#训练集
if is_train:
#按照边的类型数量将数据分组(训练集)
all_task_train_data = data_convert(all_task_train_data, 1)
#取出边类型的数据(训练集)
self.data = all_task_train_data[task_id]
#测试集
else:
#按照边的类型数量将数据分组(测试集)
all_task_val_data = data_convert(all_task_val_data, 1)
#取出边类型的数据(测试集)
self.data = all_task_val_data[task_id]
def __getitem__(self, index):
#构建邻接表
am = create_adjacency_matrix(self.data[index][0], self.n_node, self.n_edge_types)
annotation = self.data[index][1]
target = self.data[index][2] - 1
return am, annotation, target
def __len__(self):
return len(self.data)
下面是具体把dataset中的邻接矩阵打印出来的结果,第一大行对应第一个类型,左边两个红框是入度,右边两个是出度,由于是类型1,然后对应的数据为:
1 1 2(1和2有一个类型为1的边)
2 1 3(2和3有一个类型为1的边)
? 1 2 1
第二行对应的数据为:
4 1 3
3 1 2
? 1 3 4
train.py
import torch
from torch.autograd import Variable
def train(epoch, dataloader, net, criterion, optimizer, opt):
net.train()
for i, (adj_matrix, annotation, target) in enumerate(dataloader, 0):
net.zero_grad()
#计算要补0的维度
padding = torch.zeros(len(annotation), opt.n_node, opt.state_dim - opt.annotation_dim).double()
#进行padding
init_input = torch.cat((annotation, padding), 2)
if opt.cuda:
init_input = init_input.cuda()
adj_matrix = adj_matrix.cuda()
annotation = annotation.cuda()
target = target.cuda()
init_input = Variable(init_input)
adj_matrix = Variable(adj_matrix)
annotation = Variable(annotation)
target = Variable(target)
# init_input是annotation经过padding得来的,相当于h^0,经过一层GGNN后变成h^1,最后经过T层后得到h^T
# annotation还是原生态的初始化的标注信息,还没有padding
output = net(init_input, annotation, adj_matrix)
loss = criterion(output, target)
loss.backward()
optimizer.step()
if i % int(len(dataloader) / 10 + 1) == 0 and opt.verbal:
print('[%d/%d][%d/%d] Loss: %.4f' % (epoch, opt.niter, i, len(dataloader), loss.data[0]))
test.py
略
作业
【思考题】将实践的代码与论文中的公式对应起来,回顾模型是如何实现的。
【代码实践】为算法设置不同的参数,GGNN的层数(T)等参数对模型的影响;bAbl其他任务、问题类型的实验。
【总结】总结GGNN的关键技术以及如何代码实现。
标签:GGNN,GNN.09,self,带读,list,state,edge,data,out
来源: https://blog.csdn.net/oldmao_2001/article/details/112222067