格密码LLL算法：如何解决最短向量SVP问题（2）
目录
一. LLL约化基的第一条向量
二. LLL算法
三. LLL算法的正确性
四. 分析算法运行的时间
4.1 算法迭代的次数与M呈现多项式时间关系。
4.2 算法每次迭代的时间与M呈现多项式时间关系。
结论
一. LLL约化基的第一条向量
如果
为某
约化基，那么LLL约化基的第一条向量是相对短的，如下：
当
时，结论简化为
，此定义可以看成LLL约化基的必备性质之一。
证明：
给定任意格基
依据格密码的基本理论，可得：
由此可归纳出：
上式中的最后一个等号遵循了
。当i遍历所有的取值时，可得：
加入格中最小值min的性质，可得：
到此证明完毕。
对此性质的理解：该约化基性质进一步限制了SVP问题的下限，当确定了约化基，就可以输出第一条向量，该向量的长度就可以作为SVP问题的近似解，近似比为
。
二. LLL算法
第一张照片拍摄于1982年2月27日，第二张照片拍摄于2007年6月29日。从左到右依次为Peter van Emde Boas, Laszlo Lovasz, Hendrik Lenstra, Arjen Lenstra。
LLL算法的具体流程如下：
输入：整数格基
第一步：计算正交基
第二步：约化步骤。如下：
for i=2 to n
for j=i-1 to 1
第三步：置换步骤。如下：
若存在
，则置换
和
。
并返回到第一步；
输出：
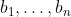
备注：此算法中
符号代表取最接近的整数，例如
，且对任意实数取整，都有如下结论：
对此算法流程的理解：第三步的置换步骤保证输出的结果满足LLL约化基的性质2。第二步的约化步骤保证满足LLL约化基的性质1。如果将上述过程进行简化的话，可得如下：
在约化迭代时，仅仅操作了列变换
，所以保证了整个过程的Gram-Schmidt正交基不变。有两个for对应内循环和外循环，当外循环处在第i轮迭代时，对于j
上的投影最大值不超过
，通过线性代数中矩阵的相减运算也可以得到此结论，此处不做过多赘述。
考虑外循环迭代到第i次，内循环迭代到j=2时为例子，矩阵B如下：
当j=2时，相当于每一列都减去整数倍的第二列，以此来保证每一列的第二个数的值最大不超过
，以此迭代类推。
三. LLL算法的正确性
LLL算法输出的约化基与相应正交基形成的格一样，且输出满足约化基的两个性质。
证明：
证明的关键是要说明此算法的输出满足约化基的两条性质且还是原格L(B)的格基。在进行置换操作时，就保证了算法的输出满足LLL约化基的性质2。在进行约化迭代操作时，仅仅进行了矩阵的基础列操作，此举不会改变格，如下：
当i>j，考虑外循环的第i次迭代中的内循环第j次迭代时，
有如下结论：
第一个等号依据规约步骤的理解。最后一个不等号依据向量与投影相乘的结论：
到此，分析完毕。
四. 分析算法运行的时间
算法总运行时间的分析分成两步，第一步需要限定总迭代的次数，第二步需要限定单次迭代所需要的时间。两步都是多项式时间，才能证明此算法的总运行时间与输入的规模之间呈现多项式关系。对于输入的n个向量，每个向量至少需要一个比特位来表示，所以n个向量至少需要n个比特位来表示。对于长度为r的向量，表示此长度需要 log r 比特位，例如长度为8的向量，至少需要log(8)=3个比特位来表示。所以给定输入规模的表达式如下：
最终算法的总运行时间是关于M的多项式关系，后续的分析也是基于此。
4.1 算法迭代的次数与M呈现多项式时间关系。
证明：
在计算机中为了方便表示格基，可以将任意格基单一映射到某个整数，该映射函数可以取名为“potential function”。
给定
为格
的格基,定义子格
如下：
令
代表格基
形成的格，理解上子格 如下：
易得，初始值满足如下不等式：
该初始值的对数运算满足M的多项式关系。在递归操作时，不改变正交基形成的格，所以也是不变的，所以需要将重心放在置换操作步骤上。
当和进行置换时，令
分别代表置换后的新值。由此可得：
此运算最后一个不等式遵循置换操作的性质。
此结果说明，在每次置换迭代时，都会缩小
倍，一直迭代到1时停止，由此可计算迭代次数如下：
上述运算过程需要使用到换底公式，如下：
对于任意的常数
（根据之前的理解
取值在1/4到3/4之间），此迭代次数都是关于M的多项式关系。
证明完毕。
取一个最接近1的
，此时的运行时间也是多项式关系的。此时对应的则为LLL算法输出的最接近的近似比值为
，此比值可以参照第一条性质进行运算理解，如果想进一步获得更好的比值，则需要用到Schnorr算法。
4.2 算法每次迭代的时间与M呈现多项式时间关系。
在每次迭代时，只进行了加减乘除运算，很明显单独看运算过程与M肯定呈现多项式时间关系。但此结果还不足够，还需要说明每一步迭代运算产生的结果的值也可以多项式时间比特表示。
考虑一个简单的例子：
（平方算法的例子）当给定一个数x时，每次都对该数进行平方运算，进行n次，判定该算法是否为多项式时间算法。
解：
操作步骤为n次，为多项式时间比特可表示。经历n次重复平方后，数x变成
，表示该数需要的比特数为
。很明显该算法的时间复杂度为
，为指数形式，非多项式时间算法。
首先易得可以利用多项式时间算法计算Gram-Schmidt正交化后的向量
，且对任意
，都有如下结论：
第二个性质说明正交化的长度有一个上限。该上限长度表示为多项式时间比特为
，且初始值
也为关于M的多项式时间比特可表示，且随后开始不断衰减。最终可得Gram-Schmidt正交向量每一步都可以多项式时间算法表示。
证明：
首先依据正交基的性质，可得如下结论：
进一步将该性质写为：
此过程可以理解为需要找到这样的
，且保证
与剩下的
都要垂直。由此可得：
将上述两个式子结合在一起可得：
将l的取值从1到i-1，由此可得到i-1个变量的i-1个方程组，如下：
很明显该线性方程组多项式时间内可解决。
结论
1980年10月21日，Hendrik Lenstra手动给Alberto Marchetti Spaccamela 演示LLL算法 ，如下图：
1980年11月10日，Arjen Lenstra 曾就算法相关的内容进行硕士答辩。当时硕士答辩委员会的组成成员有：J.Dekker, Peter van Emde Boas, Hendrik Lenstra。如下图：
每一篇重要的论文出现时，都将推动着格基约化算法的发展。其中具有重要转折点意义影响的进展有如下：
