Python手撸机器学习系列（九）：硬间隔SVM（对偶形式SMO算法求解）

原始形式梯度下降法求解请参考我的上一篇博客： 硬间隔SVM原始形式梯度下降法求解

1、对偶形式求解原理

引入拉格朗日乘子法
$$L(w,b,\lambda )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^N{\lambda }_i(1-y_i(w^T{x}_i+b))$$
则原问题可以写作：
$$\begin{gathered} \underset{w,b}{\min }\underset{\lambda }{\max }L(w,b,\lambda ) \\ s.t.{\lambda }_i\ge 0 \end{gathered}$$
这样写的好处在于：任取一点$(x_i,y_i)$

当$1-y_i(w^T{x}_i+b)>0$时，$\underset{\lambda }{\max }L(w,b,\lambda )=+\infty$，而当当$1-y_i(w^T{x}_i+b)<=0$时，$\underset{\lambda }{\max }L(w,b,\lambda )=\frac{1}{2}||w|{|}^2$

这样$\underset{w,b}{\min }\underset{\lambda }{\max }L(w,b,\lambda )=\underset{w,b}{\min }(+\infty ,\frac{1}{2}||w|{|}^2)=\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$

相当于把不符合条件的点给筛除，而且将约束条件写在了$L$里，把带约束的原问题变为无约束的原问题

但现，我们首先就要面对带有需要求解的参数$w,b$的方程，而$\lambda$又是不等式约束，这个求解过程不好做。所以，我们需要使用拉格朗日函数对偶性，将最小和最大的位置交换一下，这样就变成了：
$$\begin{gathered} \underset{\lambda }{\max }\underset{w,b}{\min }L(w,b,\lambda ) \\ s.t.{\lambda }_i\ge 0 \end{gathered}$$
要实现这样的转化，需要满足两个条件：

1. 是凸优化问题
2. 满足KKT条件

显然我们以及满足了第一个条件，而要满足第二个条件，即要求：
$$\{\begin{array}{l}\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0\\ {\lambda }_i(1-y_i(w^T{x}_i+b))=0\\ {\lambda }_i\ge 0\\ 1-y_i(w^T{x}_i+b)\le 0\end{array}$$
让我们重新回到原问题，对于$w,b$而言，$\underset{w,b}{\min }L(w,b,\lambda )$是一个无约束问题，那么对他两求偏导就好了：

对$b$求偏导，$\frac{\partial L}{\partial b}=\sum _{i=1}^N{\lambda }_i{y}_i=0$，其中（$||w|{|}^2$可以写作$w^{T}w$）

带入$L(w,b,\lambda )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^N{\lambda }_i(1-y_i(w^T{x}_i+b))$，得：
$$L(w,b,\lambda )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{w}^T{x}_i$$
再对$w$求导，$\frac{\partial L}{\partial w}=w-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i=0$，可得$w=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i$

带入$L$，得：
$$L(w,b,\lambda )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\lambda }_i$$
最后得到：
$$\begin{gathered} \underset{w,b}{\min }\underset{\lambda }{\max }L(w,b,\lambda )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\lambda }_i \\ s.t.{\lambda }_i\ge 0,\sum _{i=1}^N{\lambda }_i{y}_i=0 \end{gathered}$$
其中，$\lambda =\{{\lambda }_1,{\lambda }_2...,{\lambda }_N\}$为一组向量

在求梯度时已经得到$w=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i$，而对于支持向量$(x_k,y_k)$，总有$1-y_k(w^T{x}_k+b)=0$，转化一下：
$$\begin{array}{rl}{y}_k(w^T{x}_k+b)& =1\\ y_k^2(w^T{x}_k+b)& =y_k\\ w^T{x}_k+b& =y_k\\ b& =y_k-w^T{x}_k\end{array}$$
即最后可根据$\lambda$算出$w$和$b$，即确定分离超平面。
而求解$\lambda$，需要用到SMO算法

2、SMO算法求$\lambda$

2.1 原始解

对于对偶问题
$$\begin{gathered} \underset{\lambda }{\max }L(w,b,\lambda )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\lambda }_i \\ s.t.{\lambda }_i\ge 0,\sum _{i=1}^N{\lambda }_i{y}_i=0 \end{gathered}$$
SMO算法每次选择一对变量$({\lambda }_i,{\lambda }_j)$优化，剩下的固定

在优化中，谨记$y_i\cdot y_i=1$，这个式子可以正反互相转化，在SMO中多处用到

假设选取${\lambda }_1，{\lambda }_2$进行优化，${\lambda }_3,{\lambda }_4,...,{\lambda }_N$固定，做常数处理，将SVM的优化问题展开可得：
$$W({\lambda }_1,{\lambda }_2)={\lambda }_1+{\lambda }_2-\frac{1}{2}{K}_{1,1}{y}_1^2{\lambda }_1^2-\frac{1}{2}{K}_{2,2}{y}_2^2{\lambda }_2^2-K_{1,2}{y}_1{y}_2{\lambda }_1{\lambda }_2-y_1{\lambda }_1\sum _{i=3}^N{\lambda }_i{y}_i{K}_{i,1}-y_2{\lambda }_2\sum _{i=3}^N{\lambda }_i{y}_i{K}_{i,2}+C$$
其中$C$表示与${\lambda }_1,{\lambda }_2$无关的常数，$K_{i,j}$表示$x_i^T{x}_j$，即$x_i,x_j$的内积

根据条件$\sum _{i=1}^N{\lambda }_i{y}_i=0$，可得：

${\lambda }_1{y}_1+{\lambda }_2{y}_2=-\sum _{i=3}^N{\lambda }_i{y}_i=\zeta$

两边同乘$y_1$,由于$y_i\cdot y_i=1$可得

${\lambda }_1=y_1\zeta -{\lambda }_2{y}_1{y}_2$

即得到一个${\lambda }_i$的值可以换算出另一个

为了便于计算，我们引入：
$$\begin{gathered} v_1=\sum _{i=3}^N{\lambda }_i{y}_i{K}_{i,1} \\ {v}_2=\sum _{i=3}^N{\lambda }_i{y}_i{K}_{i,2} \end{gathered}$$
联合${\lambda }_1、{\lambda }_2$的关系式带入$W({\lambda }_1,{\lambda }_2)$中，得：
$$W({\lambda }_2)=-\frac{1}{2}{K}_{1,1}(\zeta -{\lambda }_2{y}_2{)}^2-\frac{1}{2}{K}_{2,2}{\lambda }_2^2-y_2(\zeta -{\lambda }_2{y}_2){\lambda }_2{K}_{1,2}-v_1(\zeta -{\lambda }_2{y}_2)-v_2{y}_2{\lambda }_2+\zeta y_1-{\lambda }_2{y}_1{y}_2+{\lambda }_2+C$$
就变为了只包含${\lambda }_2$的式子，此时可直接对${\lambda }_2$求导：
$$\begin{array}{rl}\frac{\partial W({\lambda }_2)}{\partial {\lambda }_2}& =K_{1,1}{y}_2(\zeta -{\lambda }_2{y}_2)-K_{2,2}{\lambda }_2+2K_{1,2}{\lambda }_2-K_{1,2}{y}_2\zeta +v_1{y}_2-v_2{y}_2-y_1{y}_2+1\\ & =-(K_{1,1}+K_{2,2}-2K_{1,2}){\lambda }_2+K_{1,1}\zeta y_2-K_{1,2}{y}_2\zeta +v_1{y}_2-v_2{y}_2-y_1{y}_2+1\end{array}$$
这里需要变换一下，使得我们能使用更新前的${\lambda }_2^{old}$表示更新后的${\lambda }_2^{new}$，而不是难以计算的$\zeta$

SVM模型对数据点的预测为：$f(x)=\sum _{i=1}^N{\lambda }_i{y}_{i}K(x_i,x)+b$

注意，在对偶形式中，可以看做将原始形式的$w^{T}x$替换为$\sum _{i=1}^N{\lambda }_i{y}_{i}K(x_i,x)$

则$v_1,v_2$可以表示为：
$$\begin{gathered} v_1=\sum _{i=3}^N{\lambda }_i{y}_i{K}_{1,i}=f(x_1)-{\lambda }_1{y}_1{K}_{1,1}-{\lambda }_2{y}_2{K}_{1,2}-b \\ {v}_2=\sum _{i=3}^N{\lambda }_i{y}_i{K}_{2,i}=f(x_2)-{\lambda }_1{y}_1{K}_{1,2}-{\lambda }_2{y}_2{K}_{2,2}-b \end{gathered}$$
且已知${\lambda }_1=(\zeta -{\lambda }_2{y}_2)y_1$，可得：
$$v_1-v_2=f(x_1)-f(x_2)-\zeta K_{1,1}+\zeta K_{1,2}+(K_{1,1}+K_{2,2}-2K_{1,2}){\lambda }_2{y}_2$$
将$v_1-v_2$的表达式带入$\frac{\partial W({\lambda }_2)}{\partial {\lambda }_2}$中，得：

$\frac{\partial W}{\partial {\lambda }_2}=-(K_{1,1}+K_{2,2}-2K_{1,2}){\lambda }_2^{new}+(K_{1,1}+K_{2,2}-2K_{1,2}){\lambda }_2^{old}+y_2(y_2-y_1+f(x_1)-f(x_2)$

在这里，$v_1$和$v_2$中的${\lambda }_2$是初始化（或更新前）确认的值，${\lambda }_2$，记为${\lambda }_2^{old}$，而求导求出的值是新的${\lambda }_2$，记为${\lambda }_2^{new}$

为了进一步精简式子，我们记$E_i$为数据$x_i$SVM预测值与真实值之间的误差：$E_i=f(x_i)-y_i$

令$\eta =K_{1,1}+K_{1,2}-2K_{1,2}$，得：
$$\frac{\partial W({\lambda }_2)}{\partial {\lambda }_2}=-\eta {\lambda }_2^{new}+\eta {\lambda }_2^{old}+y_2(E_1-E_2)=0$$
得：
$${\lambda }_2^{new}={\lambda }_2^{old}+\frac{y_2(E_1-E_2)}{\eta }$$
这样便通过旧的${\lambda }_2$获得了新的${\lambda }_2$，再根据两个因子之间的关系求出更新后的${\lambda }_1$

2.2 对原始解进行修剪

上述得到的原始解${\lambda }_2^{new}$是未考虑约束条件得到的，记为${\lambda }_2^{new,unclipped}$

但在SVM中有约束，即：
$$\{\begin{array}{l}{\lambda }_1{y}_1+{\lambda }_2{y}_2=\zeta \\ 0\le {\lambda }_i\le C\end{array}$$
说明：这里的C是在软间隔SVM中的惩罚因子，在硬间隔SVM中可以看作无穷大
画成图：

说明：其实这里的$k$就是公式中的$\zeta$

边界为边长为$C$的正方形，而${\lambda }_1$和${\lambda }_2$的约束可以用图中平行于对角线的红蓝两条线表示

当$y_1\ne y_2$的时候，设$y_1-y_2=k$

由于直线可以平行移动，所以分情况讨论，当直线在对角线下侧时（k>0），此时

${\lambda }_2$的下界$L$为0，上界$H$为$C-k=C-{\lambda }_1+{\lambda }_2$

而当直线在对角线上侧时(k<0)，此时

${\lambda }_2$的下界$L$为$-k={\lambda }_2-{\lambda }_1$，上界$H$为$C$

写在一起：
$$\{\begin{array}{l}L=max(0,{\lambda }_2-{\lambda }_1)\\ H=min(C,C+{\lambda }_2-{\lambda }_1)\end{array}$$
同理，对于$y_1=y_2$的情况，有${\lambda }_1+{\lambda }_2=k$，此时${\lambda }_2$上下界为：
$$\{\begin{array}{l}L=max(0,{\lambda }_1+{\lambda }_1-C)\\ H=min(C,{\lambda }_1+{\lambda }_2)\end{array}$$
注意，上下界中的${\lambda }_i$均为修剪之前的${\lambda }_i^{old}$

根据上下界，我们可以得到修剪后的${\lambda }_2^{new}$：
$${\lambda }_2^{new}=\{\begin{array}{ll}H& {\lambda }_2^{new,unclipped}>H\\ {\lambda }_2^{new,unclipped}& L\le {\lambda }_2^{new,unclipped}\le H\\ L& {\lambda }_2^{new,unclipped}<L\end{array}$$
最后得到${\lambda }_2^{new}$即可根据${\lambda }_1^{old}{y}_1+{\lambda }_2^{old}{y}_2={\lambda }_1^{new}{y}_1+{\lambda }_2^{new}{y}_2$得到${\lambda }_1^{new}$，即：
$${\lambda }_1^{new}={\lambda }_1^{old}+y_1{y}_2({\lambda }_2^{old}-{\lambda }_2^{new})$$
原因是这两个值都等于固定的其他值

2.2 更新$b$

因为$b$涉及到SVM中$f(x)$的计算以及误差$E_i$的计算，所以每次需要额外更新$b$

当$0<{\lambda }_1^{new}<C$时，根据$KKT$条件${\lambda }_i(1-y_i(w^T{x}_i+b))=0$ 可知此时

$y_1(w^T{x}_1+b)=1$，换算成对偶形式为：$y_1\sum _{i=1}^N{\lambda }_i{y}_i{K}_{i,1}+b=1$

即相应的数据点为支持向量

两边同时乘上$y_1$：

$\sum _{i=1}^N{\lambda }_i{y}_i{K}_{i,1}+b=y_1$

即可得$b_1^{new}$的值：
$$b_1^{new}=y_1-\sum _{i=3}^N{\lambda }_i{y}_i{K}_{i,1}-{\lambda }_1^{new}{y}_1{K}_{1,1}-{\lambda }_2^{new}{y}_2{K}_{2,1}$$
其中前两项可以变形：
$$y_1-\sum _{i=3}^N{\lambda }_i{y}_i{K}_{i,1}=-E_1+{\lambda }_1^{old}{y}_1{K}_{1,1}+{\lambda }_2^{old}{y}_2{K}_{2,1}+b^{old}$$
当$0<{\lambda }_2^{new}<C$，即可得到：

$b_2^{new}=-E_2-y_1{K}_{1,2}({\lambda }_1^{new}-{\lambda }_1^{old})-y_2{K}_{2,2}({\lambda }_2^{new}-{\lambda }_2^{old})+b^{old}$

此时他们相等，即$b^{new}=b_1^{new}=b_2^{new}$

当${\lambda }_1,{\lambda }_2$都在边界上且$L\ne H$时，$b_1,b_2$之间的值就是KKT条件的阈值，SMO算法选取中点作为新的阈值：
$$b^{new}=\frac{1}{2}(b_1^{new}+b_2^{new})$$

3、代码实现

其实只需要最后的公式，就足够写出代码了

import numpy as np
import random
import matplotlib.pyplot as plt

def simple_smo(dataset, labels, C, max_iter):
  
    dataset = np.array(dataset)
    m, n = dataset.shape #样本数量，特征数量
    labels = np.array(labels)

    # 初始化参数λ，b为0
    lambds = np.zeros(m) #每个样本都有一个λ乘子
    b = 0
    it = 0


    while it < max_iter:
        pair_changed = 0 #选取的一对值相较于之前是否有变化
        for i in range(m):
            λ_i, x_i, y_i = lambds[i], dataset[i], labels[i] #选取一组λ
            fx_i = SVM_predict(x_i,lambds,dataset,labels,b)
            E_i = fx_i - y_i
            j = select_j(i, m) #选取另一个λ
            λ_j, x_j, y_j = lambds[j], dataset[j], labels[j]
            fx_j = SVM_predict(x_j,lambds,dataset,labels,b)
            E_j = fx_j - y_j
            K_ii, K_jj, K_ij = np.dot(x_i, x_i), np.dot(x_j, x_j), np.dot(x_i, x_j)
            eta = K_ii + K_jj - 2*K_ij #
            if eta <= 0:
                print('WARNING  eta <= 0')
                continue
            # 获取更新的alpha对
            λ_i_old, λ_j_old = λ_i, λ_j #未更新前的参数
            λ_j_new = λ_j_old + y_j*(E_i - E_j)/eta
            # 对alpha进行修剪
            if y_i != y_j:
                L = max(0, λ_j_old - λ_i_old)
                H = min(C, C + λ_j_old - λ_i_old)
            else:
                L = max(0, λ_i_old + λ_j_old - C)
                H = min(C, λ_j_old + λ_i_old)
            λ_j_new = clip(λ_j_new, L, H) #根据上下界修剪
            λ_i_new = λ_i_old + y_i*y_j*(λ_j_old - λ_j_new) #根据公式反推另一个参数
            if abs(λ_j_new - λ_j_old) < 0.00001: #这个参数已经优化到最佳，换下一个
                #print('WARNING   alpha_j not moving enough')
                continue

            #更新b
            lambds[i], lambds[j] = λ_i_new, λ_j_new
            b_i = -E_i - y_i*K_ii*(λ_i_new - λ_i_old) - y_j*K_ij*(λ_j_new - λ_j_old) + b
            b_j = -E_j - y_i*K_ij*(λ_i_new - λ_i_old) - y_j*K_jj*(λ_j_new - λ_j_old) + b
            if 0 < λ_i_new < C:
                b = b_i
            elif 0 < λ_j_new < C:
                b = b_j
            else:
                b = (b_i + b_j)/2
            pair_changed += 1
            print('INFO   iteration:{}  i:{}  pair_changed:{}'.format(it, i, pair_changed))
        if pair_changed == 0: #参数优化完成，下一轮
            it += 1
        else: #参数没有优化完成，继续迭代
            it = 0
        print('iteration number: {}'.format(it))
    return lambds, b

def SVM_predict(x,lambds,data,label,b):
    "SVM分类器函数 y = w^Tx + b,即文中的f(x)"
    res = 0
    for i in range(data.shape[0]):
        res += lambds[i]*label[i]*(data[i].dot(x.T))
    return res + b


def get_w(lambdas, dataset, labels):
    #通过λ求w
    w = 0
    for i in range(len(dataset)):
        w += lambdas[i]*y[i]*dataset[i]
    return w

def clip(alpha, L, H):
    #修建λ的值到L和H之间.

    if alpha < L:
        return L
    elif alpha > H:
        return H
    else:
        return alpha

def select_j(i, m):
    #在m中随机选择除了i之外剩余的
    l = list(range(m))
    seq = l[: i] + l[i+1:]
    return random.choice(seq)

def get_point():
    x_true =  [[1,1.5],[1,3],[4,5],[2,4]]
    x_false = [[1,0.5],[4,2],[5,1],[4,1]]
    x_all = np.array(x_true+x_false)
    y = [1]*len(x_true) + [-1]*len(x_false)
    return x_all,y,x_true,x_false

def plot(x_true,x_false,w,b):
    plot_x = np.arange(0,7)
    plot_y = -(w[0]*plot_x+b)/w[1]
    plt.scatter([x[0] for x in x_true],[x[1] for x in x_true] , c='r' , label='+1')
    plt.scatter([x[0] for x in x_false],[x[1] for x in x_false] , c='b',label='-1')
    plt.plot(plot_x,plot_y,c = 'green')
    plt.xlim(0,6)
    plt.ylim(0,6)
    plt.legend()
    plt.plot()
    plt.show()

if __name__ == '__main__':
    x,y,x_true,x_false = get_point()
    lambdas, b = simple_smo(x, y, 10, 10)
    w = get_w(lambdas, x, y)
    print('-'*40+'result'+'-'*40)
    print('lambdas:{}\nw:{}\nb:{}'.format(lambdas,w,b))
    plot(x_true,x_false,w,b)

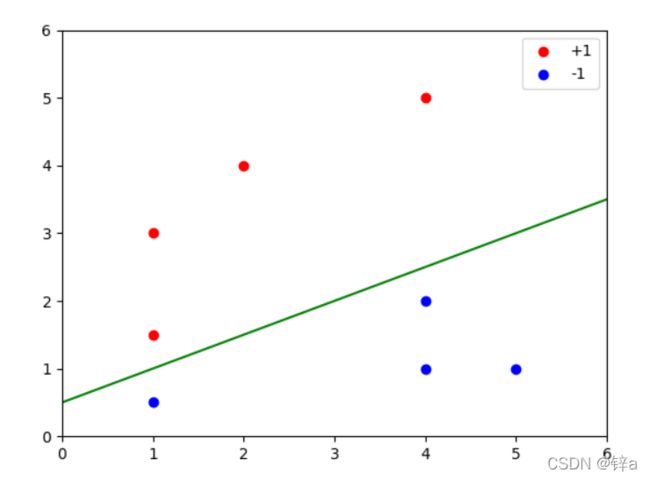
实验结果：

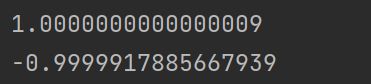
测试一下支持向量到直线的距离（忽略相同的分母）：

print(w.dot(np.array([1,1.5]))+b)
print(w.dot(np.array([1, 0.5])) + b)

结果：

除了精度上的差异，基本上已经相等

4、参考文献及联系方式

SMO算法部分参考https://zhuanlan.zhihu.com/p/29212107
对偶原理部分参考：https://www.bilibili.com/video/BV1aE411o7qd?from=search&seid=7374859475814254502&spm_id_from=333.337.0.0

以上仅为我的理解，新人自学，自知才疏学浅，如有纰漏谬误恳请指出
如有问题，欢迎评论留言，或者联系我的邮箱：
[email protected]