Python使用技巧(一):matplotlib可视化动态图
import math
import random
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
def plot_durations(y):
plt.figure(2)
plt.clf()
plt.subplot(211)
plt.plot(y[:,0])
plt.subplot(212)
plt.plot(y[:,1])
plt.pause(0.001) # pause a bit so that plots are updated
if is_ipython:
display.clear_output(wait=True)
display.display(plt.gcf())
x = np.linspace(-10,10,500)
y = []
for i in range(len(x)):
y1 = np.cos(i/(3*3.14))
y2 = np.sin(i/(3*3.14))
y.append(np.array([y1,y2])) #保存历史数据
plot_durations(np.array(y))
import matplotlib.pyplot as plt
ax = [] # 定义一个 x 轴的空列表用来接收动态的数据
ay = [] # 定义一个 y 轴的空列表用来接收动态的数据
plt.ion() # 开启一个画图的窗口
for i in range(100): # 遍历0-99的值
ax.append(i) # 添加 i 到 x 轴的数据中
ay.append(i**2) # 添加 i 的平方到 y 轴的数据中
plt.clf() # 清除之前画的图
plt.plot(ax,ay) # 画出当前 ax 列表和 ay 列表中的值的图形
plt.pause(0.1) # 暂停一秒
plt.ioff() # 关闭画图的窗口
import math
import random
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# % matplotlib
# inline
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
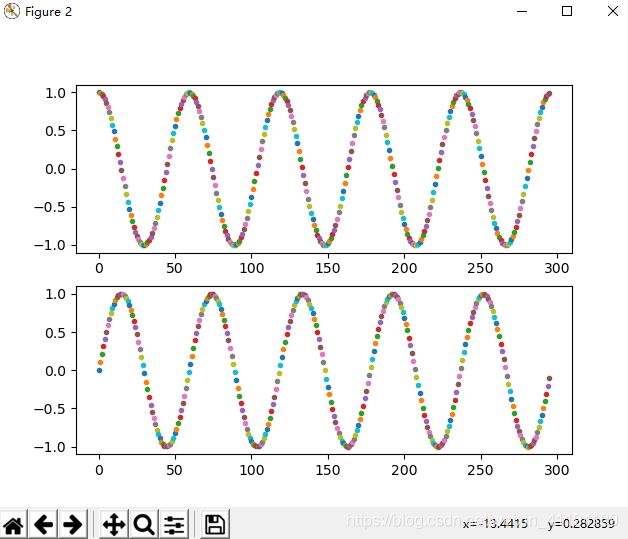
def plot_durations(i, y1, y2):
plt.figure(2)
# plt.clf() 此时不能调用此函数,不然之前的点将被清空。
plt.subplot(211)
plt.plot(i, y1, '.')
plt.subplot(212)
plt.plot(i, y2, '.')
plt.pause(0.001) # pause a bit so that plots are updated
if is_ipython:
display.clear_output(wait=True)
display.display(plt.gcf())
x = np.linspace(-10, 10, 500)
y = []
for i in range(len(x)):
y1 = np.cos(i / (3 * 3.14))
y2 = np.sin(i / (3 * 3.14))
# y.append(np.array([y1,y2])) #保存历史数据
plot_durations(i, y1, y2)
import math
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 空间三维画图
# 数据
data = np.arange(24).reshape((8, 3))
x = data[:, 0] # [ 0 3 6 9 12 15 18 21]
y = data[:, 1]*np.sin(x) # [ 1 4 7 10 13 16 19 22]
z = data[:, 2]*np.cos(x) # [ 2 5 8 11 14 17 20 23]
# 绘制散点图
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x, y, z)
# 添加坐标轴(顺序是Z, Y, X)
ax.set_zlabel('Z', fontdict={'size': 15, 'color': 'red'})
ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'red'})
ax.set_xlabel('X', fontdict={'size': 15, 'color': 'red'})
plt.show()
import math
import random
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# %matplotlib inline
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
def plot_durations(y1, y2):
plt.figure(2)
# plt.clf()
plt.subplot(211)
plt.plot(x, y1)
plt.subplot(212)
plt.plot(x, y2)
plt.pause(0.001) # pause a bit so that plots are updated
if is_ipython:
display.clear_output(wait=True)
display.display(plt.gcf())
x = np.linspace(-10,10,500)
for i in range(100):
y1 = np.cos(x*i/(3*3.14))
y2 = np.sin(x*i/(3*3.14))
plot_durations(y1, y2)
# -*- coding: utf-8 -*-
from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np
class Particle:
def __init__(self, x, y, ang_vel):
self.x = x
self.y = y
self.ang_vel = ang_vel
class ParticleSimulator:
def __init__(self, particles):
self.particles = particles
def evolve(self, dt):
timestep = 0.00001
nsteps = int(dt / timestep)
for i in range(nsteps):
for p in self.particles:
norm = (p.x **2 + p.y ** 2) ** 0.5
v_x = -p.y / norm
v_y = p.x / norm
d_x = timestep * p.ang_vel * v_x
d_y = timestep * p.ang_vel * v_y
p.x += d_x
p.y += d_y
def visualize(simulator):
X = [p.x for p in simulator.particles]
Y = [p.y for p in simulator.particles]
fig = plt.figure()
ax = plt.subplot(111, aspect = 'equal')
line, = ax.plot(X, Y, 'ro')
plt.xlim(-1, 1)
plt.ylim(-1, 1)
def init():
line.set_data([], [])
return line,
def init2():
line.set_data([], [])
return line
def animate(aa):
simulator.evolve(0.01)
X = [p.x for p in simulator.particles]
Y = [p.y for p in simulator.particles]
line.set_data(X, Y)
return line,
anim = animation.FuncAnimation(fig,
animate,
frames=10,
init_func = init,
blit = True,
interval = 10)
plt.show()
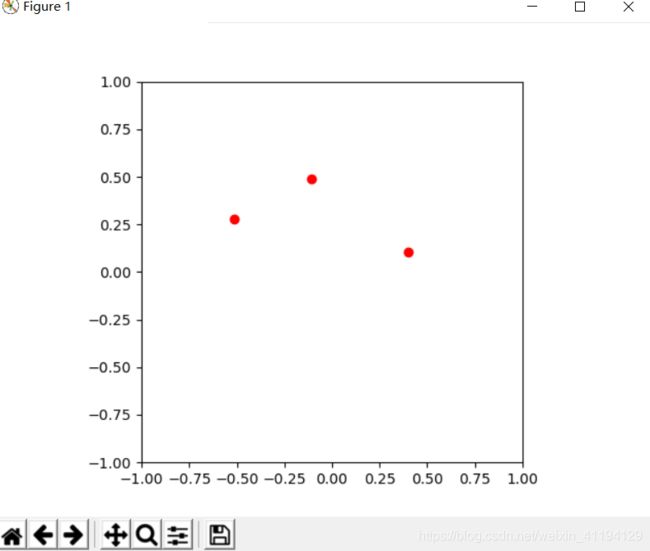
def test_visualize():
particles = [Particle(0.3, 0.5, 1),
Particle(0.0, -0.5, -1),
Particle(-0.1, -0.4, 3)]
simulator = ParticleSimulator(particles)
visualize(simulator)
if __name__ == '__main__':
test_visualize()
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.animation as animation
def update_points(num):
point_ani.set_data(x[num], y[num])
return point_ani,
x = np.linspace(0, 2 * np.pi, 100)
y = np.sin(x)
fig = plt.figure(tight_layout=True)
plt.plot(x, y)
point_ani, = plt.plot(x[0], y[0], "ro")
plt.grid(ls="--")
ani = animation.FuncAnimation(fig, update_points, frames=np.arange(0, 100), interval=100, blit=True)
plt.show()
保存为HTML格式,是不需要安装额外软件的
导入模块加上这一条:
from matplotlib.animation import HTMLWriter
最后加上这一条:
mywriter = HTMLWriter(fps=60)
ani.save('myAnimation.html',writer=mywriter)
保存为gif格式,需要下载一个imagemagick软件,找了我好久才找到软件来源imagemagick:
http://www.imagemagick.org/script/download.php#windows
下载的是dll,下载到任何文件夹下应该都可以。我安装在了python安装程序文件夹下。
代码部分相当简单,只需要在最后加一条:
ani.save('decay.gif',writer='imagemagick',fps=30)
用imagemagick保存
如果下了imagemagick,里面自带了ffmpeg的dll,那么也只需要在最后加一条:
ani.save('decay.gif',writer='ffmpeg',fps=30)
mp4:
用python库保存
如果不像下imagemagick,可以这么做:
from matplotlib.animation import FFMpegWriter
并在最后加上:
mywriter = FFMpegWriter(fps=60)
ani.save('myAnimation.MP4',writer=mywriter)