多弹协同攻击时的无源定位(一)
题目
采用被动接收方式的无源探测定位技术具有作用距离远、隐蔽接
收、不易被敌方发觉等优点,能有效提高探测系统在电子战环境下的
生存能力和作战能力。
在无源定位的研究中,测向定位技术(Direction of Arrival,DOA)
是最早出现的定位方法,通过高精度测向设备检测辐射源信号到达方
向,以各个测向线的交点作为目标位置的估计值,该方法简单易行但
定位误差一般比较大;无源时差定位(Time Difference of Arrival,
TDOA)具有定位精度高的优势,通过测量辐射源到各观测点的信号
到达时间差(即辐射源到各观测点的距离差,亦称程差),以此构建
一组关于辐射源位置的双曲线(面)方程组,求解该双曲方程组就可
以得到辐射源的坐标位置。但经典的TDOA 涉及到求解非线性方程组,
一般不易得到解析解,若预先知道目标的大致位置则有可能简化计算。
有时将TDOA 与DOA两种方法融合使用,会得到更好的定位效果。
考虑空舰导弹对水面舰船实施攻击时的无源定位问题。为保证载
机的安全性和发射的隐蔽性,只要满足基本的攻击条件,载机尽量远
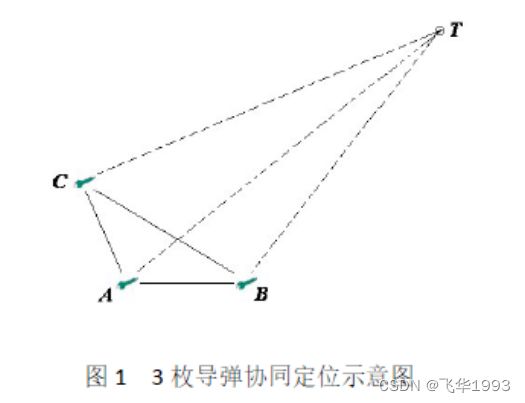
距离发射导弹。多枚导弹协同自主地搜索并攻击既定目标。如图1 所
示,3 枚导弹分别位于A、B、C 三点,目标位于T 点。在导弹导引头
雷达开机前,导弹不主动发射电磁波,只被动接收目标发射的电磁波,
实现对目标无源定位。导弹之间有数据链路保障相关信息的实时传输。
问题1 图1中,3枚导弹与目标不在同一平面,试利用导弹和目标的相
互几何位置关系,基于程差测量值和测向角度信息,构建目标定位方
法并分析哪些参数(包括3 枚导弹的空间几何构型等)对定位精度有
较大的影响?设计合理的仿真实验,验证所构建的方法的有效性。
问题2 当水面舰船目标实施机动时,如何控制3枚导弹的飞行状态(包
括相互间间距、相互连线之间的角度等队形参数,以及导弹编队与舰
船目标的空间几何位置关系等),以实现对水面舰船目标高精度的实
时定位?设计合理的仿真实验,验证所构建的方法的有效性
模型
假设第 i i i枚导弹t时刻的坐标为 ( x i t , y i t , z i t ) \left(x_{it},y_{it},z_{it}\right) (xit,yit,zit),假设第 i i i个基站的接收信号为
u i ( t ) = s ( t − d i ) + v i ( t ) , i = 1 , 2 , ⋯ , M u_i\left(t\right)=s\left(t-d_i\right)+v_i\left(t\right),i=1,2,\cdots,M ui(t)=s(t−di)+vi(t),i=1,2,⋯,M
其中, s ( t ) s(t) s(t)为目标发射的源信号, d i d_i di为源信号传播到达第i枚导弹的时延, v i ( t ) v_i(t) vi(t)为加性高斯白噪声,且假设信号和噪声相互独立。
以第一枚导弹的时延为参考基准,利用广义互相关算法(GCC)估计源信号到达第i枚导弹的时差为
d i 1 = d i − d 1 d_{i1}=d_i-d_1 di1=di−d1
设信号传输速度为c,r_i为目标到第i枚导弹的距离,信号到第i枚导弹的距离之差为
r_{i1}=cd_{i1}=r_i-r_1,i=2,3,\cdots,M
其中, r i r_i ri为声源到第i枚导弹的距离,满足
r i 2 = ( x i − x ) 2 + ( y i − y ) 2 + ( z i − z ) 2 = K i − 2 x i x − 2 y i y − 2 z i z + x 2 + y 2 + z 2 , i = 1 , 2 , ⋯ , M r_i^2=\left(x_i-x\right)^2+\left(y_i-y\right)^2+\left(z_i-z\right)^2 =K_i-2x_ix-2y_iy-2z_iz+x^2+y^2+z^2,i=1,2,\cdots,M ri2=(xi−x)2+(yi−y)2+(zi−z)2=Ki−2xix−2yiy−2ziz+x2+y2+z2,i=1,2,⋯,M
其中, K i = x i 2 + y i 2 + z i 2 K_i=x_i^2+y_i^2+z_i^2 Ki=xi2+yi2+zi2。
当导弹数为4时,可得目标点T的唯一解
[ x y z ] = [ x 21 y 21 z 21 x 31 y 31 z 31 x 41 y 41 z 41 ] − 1 [ 1 2 ( K 2 − K 1 − r 21 2 ) − r 21 r 1 1 2 ( K 3 − K 1 − r 31 2 ) − r 31 r 1 1 2 ( K 3 − K 1 − r 41 2 ) − r 41 r 1 ] \left[\begin{matrix}x\\y\\z\end{matrix}\right]=\left[\begin{matrix}x_{21} & y_{21} & z_{21} \\x_{31} & y_{31} & z_{31} \\x_{41} & y_{41} & z_{41}\end{matrix}\right]^{-1} \left[\begin{matrix}\frac{1}{2}(K_2-K_1-r_{21}^{2})-r_{21}r_1\\\frac{1}{2}(K_3-K_1-r_{31}^{2})-r_{31}r_1\\\frac{1}{2}(K_3-K_1-r_{41}^{2})-r_{41}r_1\end{matrix}\right] xyz = x21x31x41y21y31y41z21z31z41 −1 21(K2−K1−r212)−r21r121(K3−K1−r312)−r31r121(K3−K1−r412)−r41r1
令
R = [ x 21 y 21 z 21 x 31 y 31 z 31 x 41 y 41 z 41 ] − 1 R = \left[\begin{matrix}x_{21} & y_{21} & z_{21} \\x_{31} & y_{31} & z_{31} \\x_{41} & y_{41} & z_{41}\end{matrix}\right]^{-1} R= x21x31x41y21y31y41z21z31z41 −1
导弹与目标点的相对位置实时变化,本文将导弹A在初始时刻的位置记为 ( x 1 ( 0 ) , y 1 ( 0 ) , z 1 ( 0 ) ) \left(x_1(0),y_1(0),z_1(0)\right) (x1(0),y1(0),z1(0)),在另一时刻导弹A、B、C的位置分别记为 ( x 1 ( 1 ) , y 1 ( 1 ) , z 1 ( 1 ) ) \left(x_1(1),y_1(1),z_1(1)\right) (x1(1),y1(1),z1(1))、 ( x 2 ( 1 ) , y 2 ( 1 ) , z 2 ( 1 ) ) \left(x_2(1),y_2(1),z_2(1)\right) (x2(1),y2(1),z2(1))、 ( x 3 ( 1 ) , y 3 ( 1 ) , z 3 ( 1 ) ) \left(x_3(1),y_3(1),z_3(1)\right) (x3(1),y3(1),z3(1))
如果R矩阵可逆,则方程有唯一解,此时,不难得出, ( x 1 ( 0 ) , y 1 ( 0 ) , z 1 ( 0 ) ) \left(x_1(0),y_1(0),z_1(0)\right) (x1(0),y1(0),z1(0))、 ( x 1 ( 1 ) , y 1 ( 1 ) , z 1 ( 1 ) ) \left(x_1(1),y_1(1),z_1(1)\right) (x1(1),y1(1),z1(1))、 ( x 2 ( 1 ) , y 2 ( 1 ) , z 2 ( 1 ) ) \left(x_2(1),y_2(1),z_2(1)\right) (x2(1),y2(1),z2(1))、 ( x 3 ( 1 ) , y 3 ( 1 ) , z 3 ( 1 ) ) \left(x_3(1),y_3(1),z_3(1)\right) (x3(1),y3(1),z3(1))与目标点,任意4点不共面,否则方程将有无数个解,这显然无法达到精确定位的目的。所以,如果采用此方法,导弹A飞行方向所在直线与目标点相交,那么将无法得到精确解,此时可考虑采用导弹B或导弹C的初始位置作为 ( x 1 ( 0 ) , y 1 ( 0 ) , z 1 ( 0 ) ) \left(x_1(0),y_1(0),z_1(0)\right) (x1(0),y1(0),z1(0)),然而,当导弹A、B、C的飞行方向所在直线均与目标点相交时,那么就此方法将无法适用,在使用本方法时,最后应予以验证。
仿真代码
python代码
import numpy as np
import math
import matplotlib.pyplot as plt
def distance(x1,y1,z1,x2,y2,z2):
dist =math.sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)+(z1-z2)**2)
return dist
c = 340
t1 = 0.15
t2 = 0.11
t3 = 0.2
t4 = 0.91
x1 = 10
y1 = 10
z1 = 10
x2 = 240
y2 = 20
z2 = 20
x3 = 124
y3 = 250
z3 = 60
x4 = 51
y4 = 53
z4 = 244
r1 = c*t1
r2 = c*t2
r3 = c*t3
r4 = c*t4
print("distance")
print(r1,r2,r3,r4)
# r21 = r2 - r1
# r31 = r3 - r1
# r41 = r4 - r1
r21 = c*(t2-t1)
r31 = c*(t3-t1)
r41 = c*(t4-t1)
print(r21,r31,r41)
x21 = x2 - x1
x31 = x3 - x1
x41 = x4 - x1
y21 = y2 - y1
y31 = y3 - y1
y41 = y4 - y1
z21 = z2 - z1
z31 = z3 - z1
z41 = z4 - z1
# print([x21, x31, y21, y31])
P1_tmp = np.array([[x21,y21,z21],[x31,y31,z31],[x41,y41,z41]])
print("P1_tmp:")
print(P1_tmp)
P1 = (-1)*np.linalg.inv(P1_tmp)
print(P1)
P2= np.array([[r21], [r31],[r41]])
print("P2")
print(P2)
K1 = x1*x1 + y1*y1 + z1*z1;
K2 = x2*x2 + y2*y2 + z2*z2;
K3 = x3*x3 + y3*y3 + z3*z3;
K4 = x4*x4 + y4*y4 + z4*z4;
print(K1,K2,K3,K4)
P3 = np.array([ [ (-K2 + K1 + r21*r21)/2], [(-K3 + K1 + r31*r31)/2 ],[(-K4 + K1 + r41*r41)/2]])
print("P3:")
print(P3)
xy_esti = (np.dot(P1 , P2)) * r1 +np.dot( P1 , P3)
print("xy_esti")
#print(type(xy_esti[0]))
print(int(xy_esti[0]),int(xy_esti[1]),int(xy_esti[2]))
在实际仿真中,可加入验证环节,用以验证仿真的有效性。