基于群智能算法的TSP问题求解

TSP问题简介

旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。
从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。

遗传算法简介

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。
遗传算法（Genetic Algorithm）是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机化搜索方法。它是由美国的J.Holland教授1975年首先提出，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
遗传算法也是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法，是进化算法的一种。这种启发式通常用来生成有用的解决方案来优化和搜索问题。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择以及杂交等。遗传算法在适应度函数选择不当的情况下有可能收敛于局部最优，而不能达到全局最优。

粒子群算法简介

粒子群算法，又叫鸟群算法，可见是受鸟群捕食行为的启发。它属于遗传算法、群智算法。粒子群算法关注于粒子的两个属性：位置和速度。每个粒子在空间中单独搜寻，它们记得自己找到的过最优解，也知道整个粒子群当前找到的最优解。下一步要去哪，取决于粒子当前的方向、自己找到过的最优解的方向、整个粒子群当前最优解的方向。

粒子群算法流程

蚁群算法简介

蚁群算法（Ant Clony Optimization， ACO）是一种群智能算法，它是由一群无智能或有轻微智能的个体（Agent）通过相互协作而表现出智能行为，从而为求解复杂问题提供了一个新的可能性。蚁群算法最早是由意大利学者Colorni A., Dorigo M. 等于1991年提出。经过20多年的发展，蚁群算法在理论以及应用研究上已经得到巨大的进步。
蚁群算法是一种仿生学算法，是由自然界中蚂蚁觅食的行为而启发的。在自然界中，蚂蚁觅食过程中，蚁群总能够按照寻找到一条从蚁巢和食物源的最优路径。下图显示了这样一个觅食的过程。

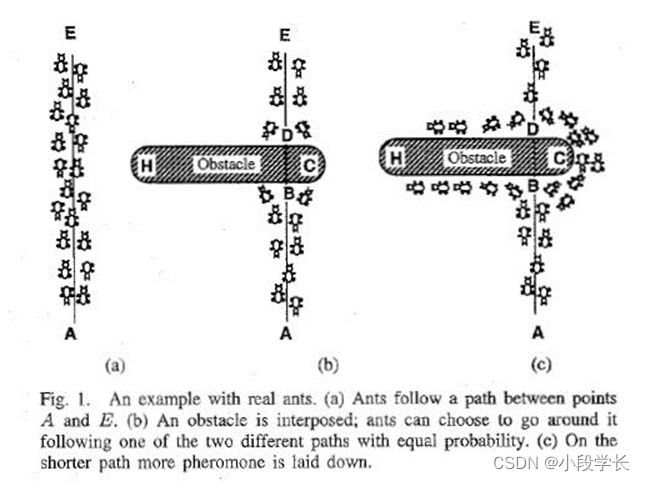
图（a）中，有一群蚂蚁，假如A是蚁巢，E是食物源（反之亦然）。这群蚂蚁将沿着蚁巢和食物源之间的直线路径行驶。假如在A和E之间突然出现了一个障碍物（图（b）），那么，在B点（或 D点）的蚂蚁将要做出决策，到底是向左行驶还是向右行驶？由于一开始路上没有前面蚂蚁留下的 信息素（pheromone） ，蚂蚁朝着两个方向行进的概率是相等的。但是当有蚂蚁走过时，它将会在它行进的路上释放出信息素，并且这种信息素会议一定的速率散发掉。信息素是蚂蚁之间交流的工具之一。它后面的蚂蚁通过路上信息素的浓度，做出决策，往左还是往右。很明显，沿着短边的的路径上信息素将会越来越浓（图（c）），从而吸引了越来越多的蚂蚁沿着这条路径行驶。
蚁群算法最早用来求解TSP问题，并且表现出了很大的优越性，因为它分布式特性，鲁棒性强并且容易与其它算法结合，但是同时也存在这收敛速度慢，容易陷入局部最优（local optimal）等缺点。
TSP问题（Travel Salesperson Problem，即旅行商问题或者称为中国邮递员问题），是一种NP-hard问题，此类问题用一般的算法是很难得到最优解的，所以一般需要借助一些启发式算法求解，例如遗传算法（GA），蚁群算法（ACO），微粒群算法（PSO）等等。

遗传算法的Python实现

import math
import random
# 得到所需二进制的位数
def get_bit(start,end,decimal):
    '''
    :param start: 区间左端点值
    :param end: 区间右端点值
    :param decimal: 有效位数
    :return: 所需二进制的位数
    '''
    # 求所需要的二进制数的位数
    need = (end - start) * pow(10, decimal + 1)
    # 对2取对数，向上取整得到位数
    bit = int(math.log(need, 2)) + 1
    return bit
 
# 编码函数
def encode(start,end,decimal,bit,num):
    '''
    :param start: 区间左端点值
    :param end: 区间右端点值
    :param decimal: 有效位数
    :param bit: 所需二进制的位数
    :param num: 需要转化的十进制数
    :return: 22位二进制数
    '''
    # # 求所需要的二进制数的位数
    # need = (end - start) * pow(10,decimal + 1)
    # # 对2取对数，向上取整得到位数
   # bit = int(math.log(need,2)) + 1
    # print(int(bit)+1)
    # 将数转化为二进制
    binary = bin(int((num + 1) * pow(10,decimal + 1)))
# 除去前面的0b
   binary = str(binary)[2:]
    # 将其补为22位
    while len(binary) < 22:
        binary = "0" + binary
    return binary
 
# 解码函数
def decode(start,end,decimal,num):
    '''
    :param start: 区间左端点值
    :param end: 区间右端点值
    :param decimal: 有效位数
    :param num: 需要解码的二进制数
    :return: 原十进制数
    '''
    num = "0b" + num
    num = int(num,2)
    num = num / pow(10,decimal + 1) -1
    # print(num)
    return num
 
# 适应度函数
def fitness(start,end,decimal,num):
    '''
    :param start: 区间左端点值
    :param end: 区间右端点值
    :param decimal: 有效位数
    :param num: 需要求适应度函数值的二进制数
    :return: 适应度函数值
    '''
    # 首先解码
    x = decode(start,end,decimal,num)
    # 计算适应度函数值
    f = x * math.sin(10 * math.pi * x) + 2.0
    return f
# 选择函数
def select(start,end,decimal,population):
    """
    :param start: 区间左端点值
    :param end: 区间右端点值
    :param decimal: 有效位数
    :param num: 需要求适应度函数值的二进制数
    :param population: 种群，规模为M
    :return: 返回选择后的种群
   """
    # 按照population顺序存放其适应度
    all_fitness = []
    for i in population:
        all_fitness.append(fitness(start,end,decimal,i))
        # print(fitness(start,end,decimal,i))
    # 适应度函数的总和
    sum_fitness = sum(all_fitness)
    # 以第一个个体为0号，计算每个个体轮盘开始的位置，position的位置和population是对应的
    all_position = []
    for i in range(0,len(all_fitness)):
        all_position.append(sum(all_fitness[:i+1])/sum_fitness)
    # print(all_position)
    # 轮盘赌进行选择
    # 经过选择后的新种群
    next_population = []
    for i in range(0,len(population)):
        # 生成0-1之间的随机小数
        ret = random.random()
        for j in range(len(all_position)):
            # 根据轮盘赌规则进行选择
            if all_position[j] > ret:
                # print(ret)
                # print(all_position[j])
                next_population.append(population[j])
                break
    return next_population
 
# 判断是否超出范围的函数
def whether_out(start,end,decimal,num):
    if start <=decode(start,end,decimal,num) <= end:
        return True
    else:
        return False
# 交叉函数
def cross(M,Pc,bit,start,end,decimal,next_population1):
    '''
    :param M: 种群规模
    :param Pc: 交叉概率
    :param bit: 二进制的位数
    :param start: 区间左端点值
    :param end: 区间右端点值
   :param decimal: 有效位数
    :param next_population1: 选择后的种群
    :return: 交叉后的种群
    '''
    num = M * Pc
    # 计数器，判断是否交换次数达到num次
    count = 0
   i = 0
    # # 交叉后的种群
    # next_population2 = []
    # 由于选择后的种群本来就是随机的，所以让相邻两组做交叉，从第一组开始直到达到交叉概率停止
    while(i < M):
        # while(count < num):
            # 随机产生交叉点
            position = random.randrange(0,bit-1)
            # print(position)
            # print(position)
            # 将两个个体从交叉点断开
            tmp11 = next_population1[i][:position]
            tmp12 = next_population1[i][position:]
            tmp21 = next_population1[i+1][:position]
            tmp22 = next_population1[i+1][position:]
            # 重新组合成新的个体
            # print(next_population1[i])
            next_population1[i] = tmp11 + tmp22
            # print(next_population1[i])
            next_population1[i+1] = tmp21 + tmp12
            # 判断交叉后的个体是否超出范围，如果每超出则count+1，否则i不加，count不加
            if (whether_out(start,end,decimal,next_population1[i]) and whether_out(start,end,decimal,next_population1[i+1])):
                i += 2
                count += 1
            else:
                continue
            if count > num:
                break
            # print(count)
return next_population1
# 取反字符串指定位置的数
def reverse(string,position):
    string = list(string)
    if string[position] == '0':
        string[position] = "1"
    else:
        string[position] = "0"
    return ''.join(string)
 
# 变异函数
def variation(M,Pm,start,end,decimal,bit,next_population2):
   # i = 0
    for i in range(M):
        ret = random.random()
        # 生成0-1的随机数，如果随机数
        if ret < Pm:
            # 随机产生变异点
            position = random.randrange(0, bit)
            next_population2[i] = reverse(next_population2[i],position)
            # if (whether_out())
            while(whether_out(start,end,decimal,next_population2[i]) == False):
                # 如果超出范围则重新随机产生变异点，直到满足范围
                position = random.randrange(0, bit)
                next_population2[i] = reverse(next_population2[i], position)
        else:
            continue
    return next_population2
# 寻找群体中的最优个体
def search(start,end,decimal,population):
    '''
    :param start: 区间左端点值
    :param end: 区间右端点值
    :param decimal: 有效位数
    :param population: 最终迭代后的群体
    :return: 最优个体
    '''
    # 记录函数值
    fit = []
    for i in population:
        fit.append(fitness(start,end,decimal,i))
    # 求出最大值所在的位置
    position = fit.index(max(fit))
    return decode(start,end,decimal,population[position])
# 测试函数
def test(M,T,Pc,Pm,start,end,decimal):
    bit = get_bit(start, end, decimal)
    # 全集，包括所有编码后的个体
   all = []
 for i in range(-1 * pow(10, 6), 2 * pow(10, 6) + 1):
        all.append(encode(start, end, decimal, bit, i / pow(10, 6)))
        i += 1
    # print(all)
    # 第一次随机选择种群，规模为T
    population = random.sample(all, M)
    # print(all)
    # print(population)
    # 进行选择操作
    next_population1 = select(start, end, decimal, population)
    # print(next_population1)
    # 进行交叉操作
    next_population2 = cross(M, Pc, bit, start, end, decimal, next_population1)
    # print(len(next_population2))
    # a = "1011101"
    # print(reverse(a,2))
    next_population3 = variation(M, Pm, start, end, decimal, bit, next_population2)
    # print(next_population2)
    # print(next_population3)
    sum = 0
    for i in range(len(next_population2)):
        if (next_population2[i] != next_population3[i]):
            sum += 1
    # print(sum)
    # print(len(next_population3))
# 主函数
def main(M,T,Pc,Pm,start,end,decimal):
  bit = get_bit(start,end,decimal)
    # 全集，包括所有编码后的个体
    all = []
    for i in range(-1 * pow(10,6), 2 * pow(10,6) + 1):
        all.append(encode(start,end,decimal,bit,i / pow(10,6)))
        i += 1
 
    # 第一次随机选择种群，规模为T
    population = random.sample(all, M)
   for i in range(T):
        # 进行选择操作
        population = select(start,end,decimal,population)
        # 进行交叉操作
        population = cross(M,Pc,bit,start,end,decimal,population )
        # 进行变异操作
        population  = variation(M,Pm,start,end,decimal,bit,population )
    # 最优个体
    final = search(start,end,decimal,population)
    print('%.5f' % final)
 
if __name__ == '__main__':
    # test()
    main(200,200,0.6,0.005,-1,2,5)

粒子群算法的Python实现

import random
import copy 
birds=int(raw_input('Enter count of bird: '))
xcount=int(raw_input('Enter count of x: '))
pos=[]
speed=[]
bestpos=[]
birdsbestpos=[]
w=0.8
c1=2 
c2=2
r1=0.6
r2=0.3
for i in range(birds):
    pos.append([])
    speed.append([])
    bestpos.append([])
def GenerateRandVec(list):
    for i in range(xcount):
        list.append(random.randrange(1,100))       
def CalDis(list):
    dis=0.0
    for i in list:
        dis+=i**2
    return dis
for i in range(birds):          #initial all birds' pos,speed
    GenerateRandVec(pos[i])
    GenerateRandVec(speed[i])
    bestpos[i]=copy.deepcopy(pos[i])
def FindBirdsMostPos():
    best=CalDis(bestpos[0])
    index=0
    for i in range(birds):
        temp=CalDis(bestpos[i])
        if temp<best:
            best=temp
            index=i
    return bestpos[index]
birdsbestpos=FindBirdsMostPos()   #initial birdsbestpos
def NumMulVec(num,list):         #result is in list
    for i in range(len(list)):
        list[i]*=num
    return list
def VecSubVec(list1,list2):   #result is in list1
    for i in range(len(list1)):
        list1[i]-=list2[i]
    return list1
 
def VecAddVec(list1,list2):      #result is in list1
    for i in range(len(list1)):
        list1[i]+=list2[i]
    return list1
def UpdateSpeed():
    #global speed
    for i in range(birds):
        temp1=NumMulVec(w,speed[i][:])
        temp2=VecSubVec(bestpos[i][:],pos[i])
        temp2=NumMulVec(c1*r1,temp2[:])
        temp1=VecAddVec(temp1[:],temp2)
        temp2=VecSubVec(birdsbestpos[:],pos[i])
        temp2=NumMulVec(c2*r2,temp2[:])
        speed[i]=VecAddVec(temp1,temp2)
def UpdatePos():
    global bestpos,birdsbestpos
    for i in range(birds):
        VecAddVec(pos[i],speed[i])
        if CalDis(pos[i])<CalDis(bestpos[i]):
            bestpos[i]=copy.deepcopy(pos[i])
    birdsbestpos=FindBirdsMostPos()
    
for i in range(100):
    #print birdsbestpos
    print CalDis(birdsbestpos)
    UpdateSpeed()
    UpdatePos()
raw_input()

蚁群算法的Python实现

import numpy as np
from tqdm import tqdm#进度条设置
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib; matplotlib.use('TkAgg')
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题

#============蚁群算法求函数极值================
 
#=======适应度函数=====
def func(x,y):
    value = 20*np.power(x*x-y*y,2)-np.power(1-y,2)-3*np.power(1+y,2)+0.3
    return value
#=======初始化参数====
m=20                   #蚂蚁个数
G_max=200              #最大迭代次数
Rho=0.9                #信息素蒸发系数
P0=0.2                 #转移概率常数
XMAX= 5               #搜索变量x最大值
XMIN= -5              #搜索变量x最小值
YMAX= 5               #搜索变量y最大值
YMIN= -5              #搜索变量y最小值
X=np.zeros(shape=(m,2)) #蚁群 shape=(20, 2)
Tau=np.zeros(shape=(m,)) #信息素
P=np.zeros(shape=(G_max,m)) #状态转移矩阵
fitneess_value_list=[] #迭代记录最优目标函数值
#==随机设置蚂蚁初始位置==
for i in range(m):#遍历每一个蚂蚁
    X[i,0]=np.random.uniform(XMIN,XMAX,1)[0] #初始化x
    X[i,1]=np.random.uniform(YMIN,YMAX,1)[0] #初始化y
    Tau[i]=func(X[i,0],X[i,1])
 
step=0.1;                #局部搜索步长
for NC in range(G_max):#遍历每一代
    lamda=1/(NC+1)
    BestIndex=np.argmin(Tau) #最优索引
    Tau_best=Tau[BestIndex] #最优信息素
     #==计算状态转移概率===
    for i in range(m):#遍历每一个蚂蚁
        P[NC,i]=np.abs((Tau_best-Tau[i]))/np.abs(Tau_best)+0.01 #即例最优信息素的距离
    #=======位置更新==========
    for i in range(m):  # 遍历每一个蚂蚁
        #===局部搜索====
        if P[NC,i]<P0:
            temp1 = X[i, 0] + (2 * np.random.random() - 1) * step * lamda # x(2 * np.random.random() - 1) 转换到【-1,1】区间
            temp2 = X[i,1] + (2 * np.random.random() - 1) * step * lamda #y
        #===全局搜索====
        else:
            temp1 = X[i, 0] + (XMAX - XMIN) * (np.random.random() - 0.5)
            temp2 = X[i, 0] + (YMAX - YMIN) * (np.random.random() - 0.5)
 
        #=====边界处理=====
        if temp1 < XMIN:
            temp1 =XMIN
        if temp1 > XMAX:
            temp1 =XMAX
        if temp2 < XMIN:
            temp2 =XMIN
        if temp2 > XMAX:
            temp2 =XMAX
        #==判断蚂蚁是否移动(选更优===
        if func(temp1, temp2) < func(X[i, 0], X[i, 1]):
            X[i, 0] = temp1
            X[i, 1]= temp2
    #=====更新信息素========
    for i in range(m):  # 遍历每一个蚂蚁
        Tau[i] = (1 - Rho) * Tau[i] + func(X[i, 0], X[i, 1]) #(1 - Rho) * Tau[i] 信息蒸发后保留的
        index=np.argmin(Tau)#最小值索引
        value=Tau[index]#最小值
    fitneess_value_list.append(func(X[index,0],X[index,1])) #记录最优目标函数值
#==打印结果===
min_index=np.argmin(Tau)#最优值索引
minX=X[min_index,0]  #最优变量x
minY=X[min_index,1]  #最优变量y
minValue=func(X[min_index,0],X[min_index,1])  #最优目标函数值
print('最优变量x',minX,end='')
print('最优变量y',minY,end='\n')
print('最优目标函数值',minValue)

plt.plot(fitneess_value_list,label='迭代曲线')
plt.legend()
plt.show()

出现的问题及解决方法

1、粒子群算法优化离散问题需要重新定义速度和位置
2、最优值计算错误：
计算更新后粒子的适应值，更新每个粒子的局部最优值以及整个粒子群的全局最优值。
3、迭代终止条件不能确定：
迭代终止条件根据具体问题而定，一般达到预定最大迭代次数或者粒子群目前为止搜寻到的最优位置满足目标函数的最小容许误差。
4、信息素常量Q：过小：会使蚁群的搜索范围减小容易过早的收敛，使种群陷入局部最优。
过大：每条路径上信息含量差别较小，容易陷入混沌状态
5、最大达代次数tmax：过小：可选路径较少，使种群陷入局部最优
过大：运算时间过长
6、蚂蚁数量m：过小：可能导致一 些从采搜紧过的路径信息紧浓度减小为0，导致过早收敛，解的全局最优性降低
过大：每条路径上信息素趋于平均，正反馈作用减弱，从而导致收敛速度减慢
7、遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码；
8、另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验；
9、算法对初始种群的选择有一定的依赖性，能够结合一些启发算法进行改进；

总结

使自己对遗传算法、粒子群算法、蚁群算法有了更进一步的了解。遗传算法是一种智能优化算法，它能较好地近似求解TSP问题，遗传算法是一类随机优化算法，但它不是简单的随机比较搜索，而是通过对染色体的评价和对染色体中基因的作用，有效地利用已有信息来指导搜索有希望改善优化质量的状态。蚁群算法(ACO)是一种用来寻找优化路径的概率型算法。这种算法具有分布计算、信息正反馈和启发式搜素的特征，本质上是进化算法中的一种启发式全局优化算法，蚁群算法中的终止条件:是否达到最大迭代次数。粒子群优化算法（PSO），粒子群中的每一个粒子都代表一个问题的可能解， 通过粒子个体的简单行为，群体内的信息交互实现问题求解的智能性。
粒子群算法同遗传算法一样，都是不稳定的，每次运行的结果都会不一致。 但是，每次运行的结果不会相差很大，最短距离都在 40 左右，以上仅仅给出了 三次结果。 粒子群算法在计算最优解会出现陷入局部最优的情况，但是它的运行效率 高，在实际的应用中有很好的效果。
欢迎大家加我微信交流讨论（请备注csdn上添加）