句法模式识别/结构模式识别（二）---形式语言

---

相关文章：
句法模式识别/结构模式识别（一）—概述
句法模式识别/结构模式识别（三）—文法推断
句法模式识别/结构模式识别（四）—句法分析
句法模式识别/结构模式识别（五）—自动机

---

句法模式识别的理论基础是乔姆斯基提出的形式语言，这篇博客就简单讲讲什么是形式语言

一、基本概念

1. 字母表：与所研究的问题有关的符号的有限集合，用V或$\sum$表示，例：${\mathbf{V}}_1=\left\{\mathbf{A},\mathbf{B},\mathbf{C},\cdots \mathbf{Z}\right\}{\mathbf{V}}_3=\left\{0,1,2\right\}$

2. 句子（链）：由字母表中符号组成的有限长度的符号串，空句用$\mathbf{\lambda }$表示

3. 句子（链）的长度：句子中所包含的符号的数目，用$\left|\cdot \right|$表示
   例：由V={a,b,c}中元素可组成的句子：
   abc，aacc，。。。等 。 所以 $\left|{\mathbf{a}}^3{\mathbf{b}}^3{\mathbf{c}}^3\right|=9$（上标3代表着重写次数）

4. 文法：在一种语言中，构成句子所必须遵循的规则的集合，用G表示。
   $\mathbf{G}=\text{（}{\mathbf{V}}_{\mathbf{N}},{\mathbf{V}}_{\mathbf{T}},\mathbf{P},\mathbf{S}\text{）}$
   这其中：
   ${\mathbf{V}}_{\mathbf{N}}$：非终止符的有限集，子模式的集合，大写字母表示（有点类似数据结构中树结构中除了叶子结点外的其他节点，不知道根节点算不算，不过这也不重要）
   ${\mathbf{V}}_{\mathbf{T}}$：终止符的有限集，基元的集合，小写字母表示（有点类似数据结构中树结构中的叶子结点）
   P：代表生成式的有限集，用文法产生句子时的重写规则
   
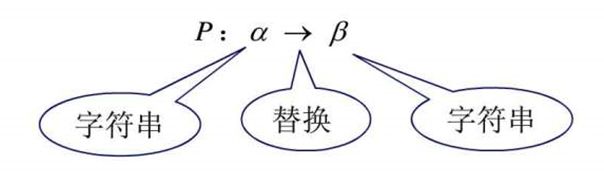
   S：起始符，代表模式本身，是一个特殊的非终止符，用生成式构成句子的时候，必须由左边是S的生成式开始

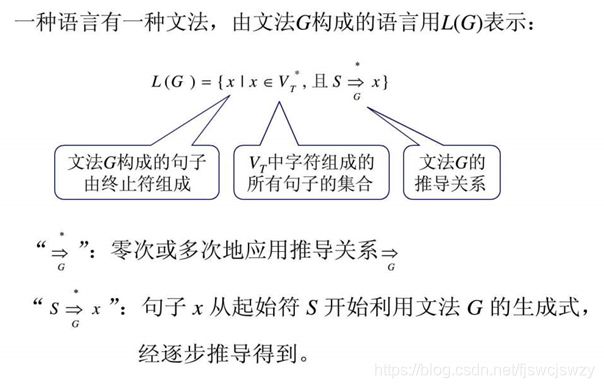
5. 语言：由字母表中的符号根据某种文法组成的句子的集合，用L表示
   ${\mathbf{V}}^{\ast }$：V中符号组成的所有句子的集合，包括空句
   ${\mathbf{V}}^{+}$：不包含空句的句子集合，${\mathbf{V}}^{\ast }={\mathbf{V}}^{+}+\left\{\mathbf{\lambda }\right\}$
   

二、文法分类

四种类型：0型文法、1型文法、2型文法、3型文法

设有文法 $\mathbf{G}=\text{（}{\mathbf{V}}_{\mathbf{N}},{\mathbf{V}}_{\mathbf{T}},\mathbf{P},\mathbf{S}\text{）}$
其中：
${\mathbf{V}}_{\mathbf{N}}$：非终止符，用大写字母表示
${\mathbf{V}}_{\mathbf{T}}$：终止符，用小写字母表示
P：产生式
S：起始符

0型文法（无约束文法）

$$\mathbf{P}\text{：}\mathbf{\alpha }\to \mathbf{\beta }$$
其中，$\mathbf{\alpha }\in {\mathbf{V}}^{+}\text{，}\mathbf{\beta }\in {\mathbf{V}}^{\ast }$

1型文法（上下文有关文法）

$$\mathbf{P}:{\mathbf{\alpha }}_1{\mathbf{A}\mathbf{\alpha }}_2\to {\mathbf{\alpha }}_1{\mathbf{\beta }\mathbf{\alpha }}_2$$
其中，${\mathbf{\alpha }}_1$和${\mathbf{\alpha }}_2$称为A的上下文，${\mathbf{\alpha }}_1\text{，}{\mathbf{\alpha }}_2\in {\mathbf{V}}^{\ast }\text{；}\mathbf{\beta }\in {\mathbf{V}}^{+}\text{，}\mathbf{A}\in {\mathbf{V}}_{\mathbf{N}}^{\ast }$（指${\mathbf{V}}_{\mathbf{N}}$的元及其组成的串）
由上下文有关文法构成的语言称为上下文有关语言，用$\mathbf{L}\left({\mathbf{G}}_1\right)$表示，${\mathbf{G}}_1$：上下文有关文法

含义：只有处于${\mathbf{\alpha }}_1$和${\mathbf{\alpha }}_2$之间的非终止符或非终止串才能被$\mathbf{\beta }$替换，并且代换后的符号数目要大于等于代换前的数目

2型文法（上下文无关文法）

$$\mathbf{P}:\mathbf{A}\to \mathbf{\beta }$$
其中$\mathbf{A}\in {\mathbf{V}}_{\mathbf{N}},\mathbf{\beta }\in {\mathbf{V}}^{+}$

3型文法（正则文法、有限态文法）

$$\mathbf{P}:\mathbf{A}\to \mathbf{a}\mathbf{B}\text{或}\mathbf{A}\to \mathbf{b}$$
其中，$\mathbf{A},\mathbf{B}\in {\mathbf{V}}_{\mathbf{N}}\text{，}\mathbf{a},\mathbf{b}\in {\mathbf{V}}_{\mathbf{T}}$

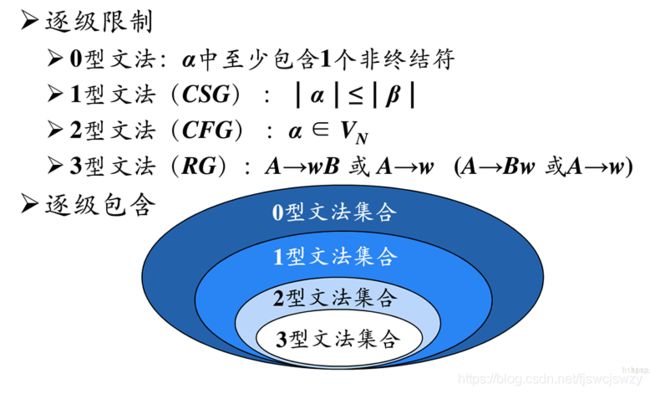后一种文法的限制比前一种文法的限制严格；
限制越多的文法越容易推断；
句法模式识别中多采用上下文无关文法和正则文法

三、模式的描述方法

根据结构特征对模式进行描述。—叫做结构描述法（又称句法表示法）
模式的表示：链表示法、树表示法、图表示法
对应的文法：链文法（串文法）、树文法、图文法

基元的确定

目前关于基元的确定还没有一个通用的解决办法，更多是依赖经验，基元的选择遵循两个基本原则：

1. 基元应是模式的基本单元，能够通过一定的结构关系对数据进行紧凑、方便的描述。
2. 基元应该容易用现有的非句法方法进行提取或识别。例如语音识别中—音素；识别手写文字—笔划

模式的链表示法

1、链码法

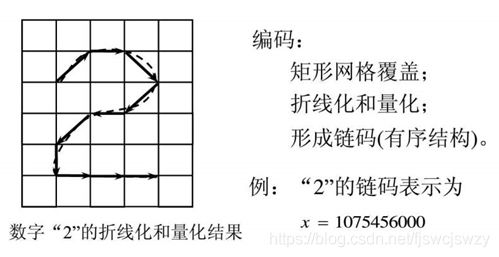
2、图形描述语言法（PDL）
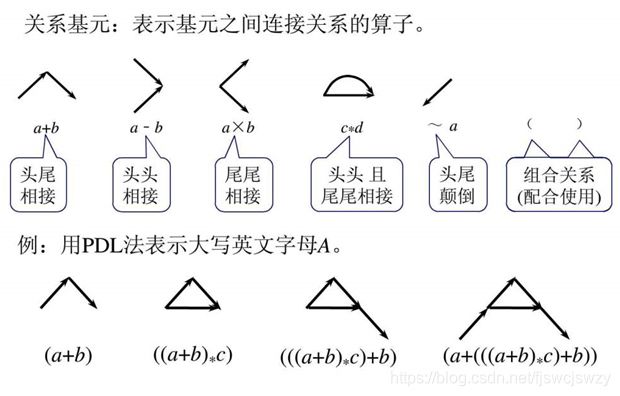链表示法：只能从左边或右边与其他符号相连，是一维连接方式

模式的树表示法

是一个高维表示法