【自监督学习合集】一:moco代码精读
目录
- 写在前面
- 一、moco的主要思想
- 二、代码精读
-
- 2.1 代码结构
- 2.2 main_moco.py
-
- 2.2.1 参数设置
- def main():
- def main_worker(gpu, ngpus_per_node, args)
- def train(train_loader, model, criterion, optimizer, epoch, args)
- 2.3 moco文件夹
-
- 2.3.1 loader.py
- 2.3.2 builder.py
-
- 模型初始化
- 样本队列
- 动量编码器
- 模型前向过程
- 2.4 main_cls.py
写在前面
本人刚入门自监督学习,对自监督学习的了解还停留在理论阶段,现在想为自己开一个坑,即这个自监督学习代码阅读合集,一方面可以加深自己的理解,另一方面也希望能帮助到与我一样的初学者,有什么不对的地方还希望大家不吝指教。
一、moco的主要思想
在说moco之前,要知道何为对比学习。对比学习是自监督学习下的一个重要分支,自监督学习就是在自身数据集上,挖掘监督的信息,通过自身产生的监督信息来训练模型,打个比方,将一张图片切成9宫格,为每宫格打上1-9的标签,之后将9宫格和标签打乱,以打乱的图片作为输入,打乱的标签作为ground truth,这样就可以通过完全自动的方式,为不带标签的数据集生成“标签”,供模型学习。 因此自监督学习的第一个关键点就是,如何挖掘无标签数据集的监督信息? 由于自监督学习是用有监督的方法训练一个无监督模型,挖掘到监督信息后,还需要考虑如何利用这些信息,这就是自监督学习的第二个关键点:如何设计合理的代理任务来挖掘数据中的潜在特征。
对比学习给出了第一个问题的解决方案:将一张图片经过不同的增强(裁剪、加噪点等)后,将这些增强后的图片视为正样本对。

moco是对比学习中最经典的模型之一,它是一个基于正负样本的对比学习方法,在基于正负样本的对比学习算法中,负例一般为一个样本库中的其他图片,虽然这个样本库不尽相同,但这些模型都在尝试不同的方法让正样本在映射空间上足够近,而负样本在映射空间上足够远,这就是个体判别的代理任务,通俗来讲就是每个样本自成一类,有多少个样本就有多少个类。MOCO将基于正负样本的对比学习归纳为字典查询问题(dictionary look-up),而这个问题的关键点是如何生成一个又大又一致的字典。
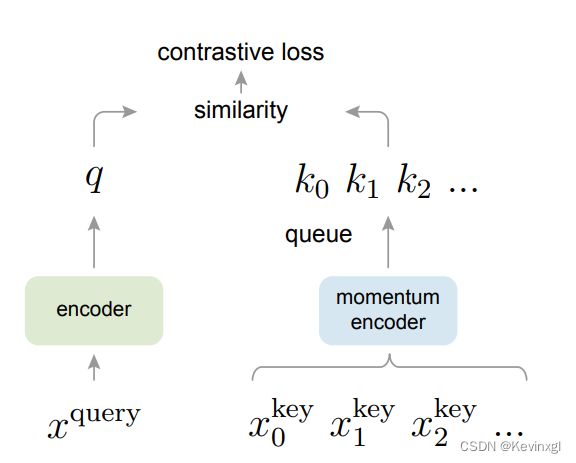
先解释一下字典查询问题,字典中的数据由键(key)和值(value)组成,在对比学习中,可以把图片想象为键,图片对应的潜在特征为值,比对时,我们拿增强后某一张图片在这个字典中查询与它来自于同一张图片但经过不同增强后的键,如果匹配成功,那它们的值也应该尽量接近,这个问题的关键点分为两部分:大和一致性,在前人的研究中,首先是大:这个字典要么太小(一个mini-batch)要么太大(整个数据集),因此需要在这两者之间权衡,moco的解决方案是样本队列,这个队列中保存固定数量的mini-batch,每有一个新的mini-batch加入到样本队列中时,就让最老的出队;然后是一致性:对比学习的模型是时刻更新的,因此每个样本经过不同时刻的模型后,所得到的特征不具有一致性,这样在不同的epoch,同一样本用于训练的特征也是不一样的,MOCO的解决方案是动量编码器,即动量更新字典中样本的特征,让它一大部分来自于上一轮训练(MOCO的实验证明,99.9%的特征来自于上一轮,效果较好),再加上样本队列每次都淘汰最老的样本,最老的样本动量更新最多,不一致性也就最高,通过这样的方法就能保证样本队列中特征的一致性。

二、代码精读
2.1 代码结构
代码分为两个文件夹和若干文件,其中文件夹detection是做目标检测下游任务的,文件夹moco是模型的主干部分,builder,主文件夹下,main_moco是moco的自监督训练过程,main_lincls则是为图片分类任务训练一个简单的线性分类器。
我们的阅读过程为:
main_moco.py->moco文件夹->main_cls.py (->detection文件夹)
2.2 main_moco.py
2.2.1 参数设置
model_names = sorted(name for name in models.__dict__
if name.islower() and not name.startswith("__")
and callable(models.__dict__[name]))
model_names是torch中不同的视觉骨干网络名,不同的参数含义如下表:
| 参数名 | 参数意义 |
|---|---|
| data | 数据集路径 |
| arch | 骨干网络,model_names选其一 |
| workers | dataloader里的参数 |
| epochs | 训练eopch |
| start-epoch | 起始epoch,一般为0,要是在某个epoch运行断掉了,可以启用这个参数,继续训练 |
| batch-size | |
| learning-rate | 模型学习率 |
| momentum | 模型动量 |
| weight-decay | 权重衰减 |
| resume | 最新checkpoint的路径 |
| moco-dim | 输出维度 |
| moco-k | 样本队列大小(负样本大小) |
| moco-m | 字典更新的动量 |
| moco-t | softmax温度 |
def main():
main首先是处理argparser传入的不同参数,最后会在最后调用main_worker函数:
main_worker(args.gpu, ngpus_per_node, args)
这里如果全部默认的话,args.gpu=None,ngpus_per_node=gpu数量。
def main_worker(gpu, ngpus_per_node, args)
函数首先是处理多进程,然后根据参数中选择的骨干网络和一些moco的特殊参数,来构造模型。
print("=> creating model '{}'".format(args.arch))
model = moco.builder.MoCo(
models.__dict__[args.arch],
args.moco_dim, args.moco_k, args.moco_m, args.moco_t, args.mlp)
print(model)
可以看到模型用了交叉熵损失函数,并使用随机梯度下降法优化模型。
# 模型
model = torch.nn.parallel.DistributedDataParallel(model, device_ids=[args.gpu])
# 损失函数
criterion = nn.CrossEntropyLoss().cuda(args.gpu)
# 优化器
optimizer = torch.optim.SGD(model.parameters(), args.lr,
momentum=args.momentum,
weight_decay=args.weight_decay)
然后是数据处理,定义了数据增强的方式和数据标准化的方式
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
augmentation = [
transforms.RandomResizedCrop(224, scale=(0.2, 1.)),
transforms.RandomGrayscale(p=0.2),
transforms.ColorJitter(0.4, 0.4, 0.4, 0.4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
normalize
]
再就是定义了datasets和dataloader,方便后续训练,train_dataset每一条数据是同一图片经过不同增强后的样本对
train_dataset = datasets.ImageFolder(
traindir,
moco.loader.TwoCropsTransform(transforms.Compose(augmentation)))
train_loader = torch.utils.data.DataLoader(
train_dataset, batch_size=args.batch_size, shuffle=(train_sampler is None),
num_workers=args.workers, pin_memory=True, sampler=train_sampler, drop_last=True)
最后根据上面定义的基本组件,启动训练流程:
train(train_loader, model, criterion, optimizer, epoch, args)
def train(train_loader, model, criterion, optimizer, epoch, args)
这里我将多进程/时间控制等与模型训练无关的过程清除
for i, (images, _) in enumerate(train_loader):
# compute output
output, target = model(im_q=images[0], im_k=images[1])
loss = criterion(output, target)
losses.update(loss.item(), images[0].size(0))
# compute gradient and do SGD step
optimizer.zero_grad()
loss.backward()
optimizer.step()
如代码所示,model有两个数据输入,一个对应着字典查询的queue,另一个对应着字典中与该queue匹配的key
2.3 moco文件夹
moco文件夹中为moco的模型结构和数据产出
2.3.1 loader.py
loader.py非常简单,它根据2.2.1节中main_worker里定义的数据增强方式,对同一图片的两个分支实现不同的增强。
class TwoCropsTransform:
"""Take two random crops of one image as the query and key."""
def __init__(self, base_transform):
self.base_transform = base_transform
def __call__(self, x):
q = self.base_transform(x)
k = self.base_transform(x)
return [q, k]
其中,base_transform就是main_worker里定义的augmentation
2.3.2 builder.py
模型初始化
def __init__(self, base_encoder, dim=128, K=65536, m=0.999, T=0.07, mlp=False):
"""
dim: feature dimension (default: 128)
K: queue size; number of negative keys (default: 65536)
m: moco momentum of updating key encoder (default: 0.999)
T: softmax temperature (default: 0.07)
"""
super(MoCo, self).__init__()
# 基本参数
self.K = K
self.m = m
self.T = T
# create the encoders
# num_classes is the output fc dimension
self.encoder_q = base_encoder(num_classes=dim)
self.encoder_k = base_encoder(num_classes=dim)
if mlp: # hack: brute-force replacement
dim_mlp = self.encoder_q.fc.weight.shape[1]
self.encoder_q.fc = nn.Sequential(nn.Linear(dim_mlp, dim_mlp), nn.ReLU(), self.encoder_q.fc)
self.encoder_k.fc = nn.Sequential(nn.Linear(dim_mlp, dim_mlp), nn.ReLU(), self.encoder_k.fc)
for param_q, param_k in zip(self.encoder_q.parameters(), self.encoder_k.parameters()):
param_k.data.copy_(param_q.data) # initialize
param_k.requires_grad = False # not update by gradient
# create the queue
self.register_buffer("queue", torch.randn(dim, K))
self.queue = nn.functional.normalize(self.queue, dim=0)
self.register_buffer("queue_ptr", torch.zeros(1, dtype=torch.long))
这里保存的就是moco的模型,首先可以看出,queue的模型和key的模型结构上完全一致,但key模型并没有梯度回传,而是直接从queue模型复制而来,这与论文中的设计保持一致。
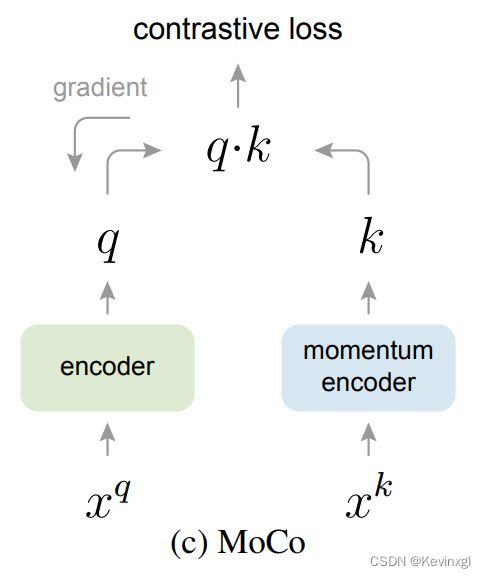
样本队列
在初始化的最后,模型还定义了样本队列,其中该队列是用队列头和列表维护的一个循环队列,该队列的入队/出队操作如下函数所示:
def _dequeue_and_enqueue(self, keys):
# gather keys before updating queue
keys = concat_all_gather(keys)
batch_size = keys.shape[0]
ptr = int(self.queue_ptr)
assert self.K % batch_size == 0 # for simplicity
# replace the keys at ptr (dequeue and enqueue)
self.queue[:, ptr:ptr + batch_size] = keys.T
ptr = (ptr + batch_size) % self.K # move pointer
self.queue_ptr[0] = ptr
每次,该队列会将队列头所指的一个batch替换为新的batch,之后将队列头指向新增batch的尾部,这样就相当于将最老的一个batch入队,新的batch添加到了队尾。
动量编码器
def _momentum_update_key_encoder(self):
"""
Momentum update of the key encoder
"""
for param_q, param_k in zip(self.encoder_q.parameters(), self.encoder_k.parameters()):
param_k.data = param_k.data * self.m + param_q.data * (1. - self.m)
param_q是通过梯度回传更新后的参数,而param_k在执行上述循环操作前则是之前的特征,self.m是动量,最佳为0.999,即样本字典中99.9%的特征都来自于之前的特征,只有0.1%来自于当前的更新,这保证了字典的高度一致性。
模型前向过程
前向过程比较常规,首先是将queue的图像通过queue编码器,得到特征:
# compute query features
q = self.encoder_q(im_q) # queries: NxC
q = nn.functional.normalize(q, dim=1)
然后动量更新key编码器,并得到key的特征:
self._momentum_update_key_encoder() # update the key encoder
k = self.encoder_k(im_k) # keys: NxC
k = nn.functional.normalize(k, dim=1)
再根据queue和key得到模型的loss,其中q和k是互为正例的,因此误差叫l_pos,而此时新的样本还没入队,所以q和样本队列中所有样本都互为负例,因此q和样本队列的误差叫做l_neg:
l_pos = torch.einsum('nc,nc->n', [q, k]).unsqueeze(-1)
l_neg = torch.einsum('nc,ck->nk', [q, self.queue.clone().detach()])
再通过torch.cat将正误差和负误差拼接起来,注意这里l_pos在前,因此正样本误差永远是每一行的第0号元素。
# logits: Nx(1+K)
logits = torch.cat([l_pos, l_neg], dim=1)
# apply temperature
logits /= self.T
由于正样本在每一行的第0号元素,在计算交叉熵的时候,输入的label代表正样本所在位置,因此label就是全0。
# labels: positive key indicators
labels = torch.zeros(logits.shape[0], dtype=torch.long).cuda()
最后,更新样本队列,老样本出队,新样本入队:
# dequeue and enqueue
self._dequeue_and_enqueue(k)
返回误差和标签后,会在main_moco.py的main_worker函数里,计算交叉熵损失,并更新queue编码器的参数。
return logits, labels
以上,就构成了一个完整的预训练过程。
2.4 main_cls.py
这一块主要是用预训练好模型,在下游任务上微调并测试,主要流程和main_moco类似,不同之处有以下几点:
模型结构不同:
main_cls中将预训练后的queue编码器直接抽取出来
'''
首先,构建骨干网络实例
'''
model = models.__dict__[args.arch]()
'''
然后,加载预训练模型,并保留queue编码器部分
'''
checkpoint = torch.load(args.pretrained, map_location="cpu")
# rename moco pre-trained keys
state_dict = checkpoint['state_dict']
for k in list(state_dict.keys()):
# retain only encoder_q up to before the embedding layer
if k.startswith('module.encoder_q') and not k.startswith('module.encoder_q.fc'):
state_dict[k[len("module.encoder_q."):]] = state_dict[k]
# delete renamed or unused k
del state_dict[k]
'''
最后,将保留的queue编码器加载到构建的实例中
'''
msg = model.load_state_dict(state_dict, strict=False)
使用部分不同:
这一块主要是模型的微调,因此并不会像训练那样对模型所有层进行梯度回传,仅对模型的线性层更新,因此需要冻住cnn层等其他层:
# freeze all layers but the last fc
for name, param in model.named_parameters():
if name not in ['fc.weight', 'fc.bias']:
param.requires_grad = False
# init the fc layer
model.fc.weight.data.normal_(mean=0.0, std=0.01)
model.fc.bias.data.zero_()
