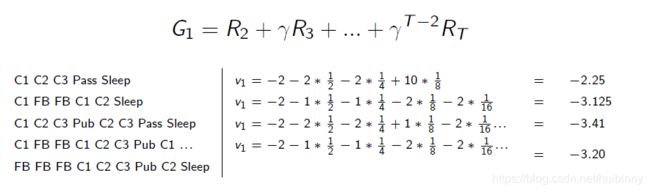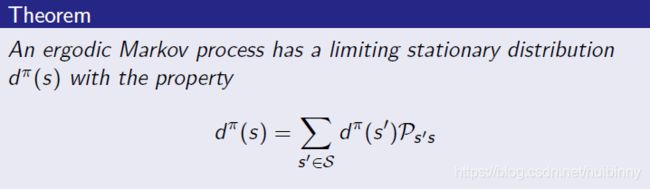David Silver强化学习笔记-Lecture 2: Markov Decision Processes

Lecture 2: Markov Decision Processes(马尔科夫决策过程)

一、Marokov Process

（一）Introduction

Introduction to MDPs

• 马尔可夫决策过程正式描述了强化学习的环境
  我们希望有一些对环境的描述。MDP可以对环境进行描述
• 环境是完全可观测的
• 也就是说当前状态完全特征化了过程
  被告知给agent的state在某种程度上特征化了整个环境展开的过程，环境的变化是依赖于一些state的，state是完全可观测的
• 所有的RL问题都可以形式化为MDPS，例如：
  • 最佳控制主要处理连续的MDP
  • 可以将部分可观察到的问题转换为MDP
  • 老虎机问题是单个状态的MDPs
    在某些时刻，你拥有一些actions的集合，你需要采取一个action，然后就可以得到该action对应的reward，之后任务就完成了。

（二）Markov Property（马尔科夫属性）

“The future is independent of the past given the present”

• 状态从历史中捕获所有相关信息
• 知道状态后，历史可能会被丢弃
• 即，状态是对未来的充分统计

State Transition Matrix（状态转移矩阵）

对于马尔可夫状态s和后继状态s‘，状态转移概率定义为：

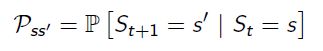
状态转移矩阵P定义了从所有状态s到所有后继状态s’的转移概率，

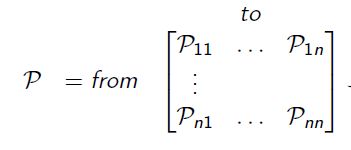
矩阵的每一行总和为1。

我们当前所处的state特征化了接下来会发生的一切，这就意味着，有一些良好定义的转移概率会告诉我，如果我之前处在这种state，就会有对应的一些概率值指出，在那种状态下我就将以一定概率值转移到一定的后继状态。例如：有一个机器人，我推了他一下，他有一定概率摔倒，或有一定概率向前走一步，这取决于之前所处的状态。

（三）马尔科夫链

Markov Process定义

马尔可夫过程是无记忆的随机过程，即具有Markov属性的一系列随机状态S1，S2 …

马尔科夫过程（或马尔科夫链）是一个元组，

• S 是一组有限的状态
• P 是状态转移概率矩阵

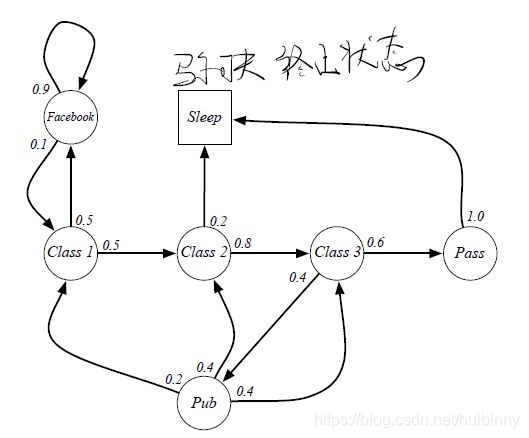
Example: Student Markov Chain

Example: Student Markov Chain Episodes

从S1 = C1开始的学生马尔可夫链样本集
S1, S2, …, ST

Example: Student Markov Chain Transition Matrix

有个这个矩阵后我们可以重复从这个矩阵中进行取样。

二、Markov Reward Process

（一）定义

马尔可夫奖赏过程是具有价值的马尔可夫链
带有value判断的Markov Process，value会告诉我们这个状态有多好。即对于一些从某个Markov Process取样得到的特定的序列，他们已经累计的多少reward。

R是当前时刻从状态S得到多少immediate reward,我们关心的是最大化累计的rewards。

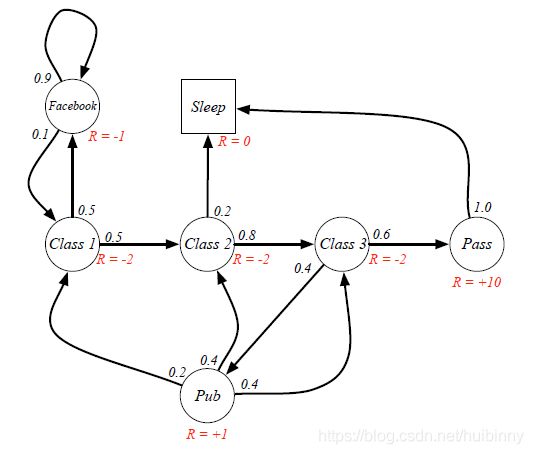
（二）Example: Student MRP

（三） Return

Gt是随机的，Gt只是一个样本，它来自我们的MRP，我们讨论的序列的rewards

• 折扣值$\gamma \in [0,1]$
• 经过k +1个时间步长后获得奖励R的值为${\gamma }^{k}R$
• 这将immediate reward为高于delayed reward。
  • $\gamma$接近0会导致“近视”评估
    越是喜欢现在的reward
  • $\gamma$接近0会导致“远视”评估
    我们越不关心现在的reward

为什么要有折扣因子

大多数马尔可夫奖赏和决策过程都被打折。 为什么？

• 数学上方便
• 避免循环马尔可夫过程中的无限收益
• 关于未来的不确定性可能无法完全体现
• 如果奖励是财务奖励，则即时奖励比延迟奖励可能会获得更多的利息
• 动物/人类行为显示出对立即奖励的偏好
• 有时可能会使用未折现的马尔可夫奖励流程（即$\gamma =1$）

即便决策过程本身包含了无限循环，单个sample都会是一个有限的连接，唯一的问题是在哪一步终止
我们没有一个关于环境的完美模型，我们认为我们已经提出了一个很不错的计划，我们认为我们确切知道如何走向未来的步骤，但如果我们不完全相信我们所做的决定，我们不完全相信我们的评估，我们可以选择打折。

（四）Value Function

value就是total reward
值函数v(s)给出状态s的长期值

MRP的状态值函数v(s)是从状态s开始的预期收益
衡量在状态s可以获得多少reward

Example: Student MRP Returns

学生MRP的return样本(随机取样)：
从S1 = C1开始,$\gamma =1$

Example: State-Value Function for Student MRP （1）

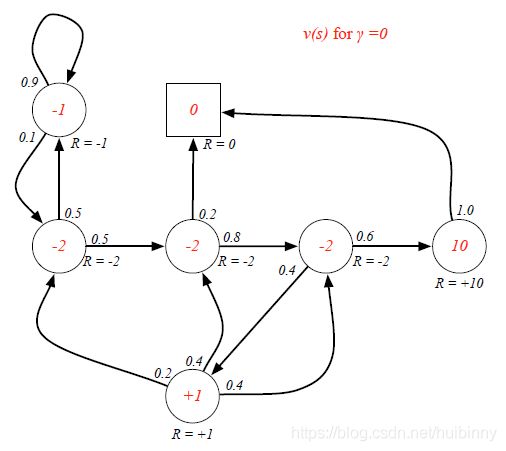
$\gamma =0$，我们完全不关心除了当前这一步其他时间步的reward

Example: State-Value Function for Student MRP （2）

$\gamma =0.9$，我们必须关心所有的state

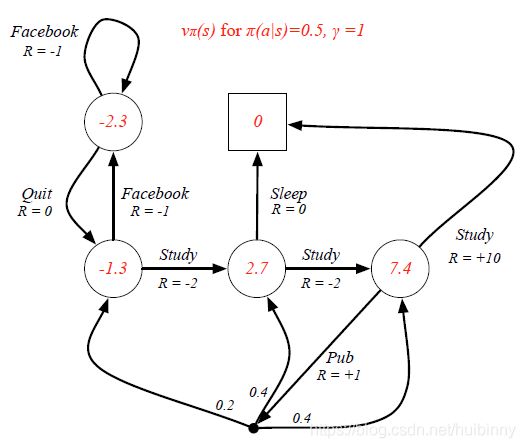
Example: State-Value Function for Student MRP （3）

$\gamma =1$，所有的state同等重要

（五）Bellman Equation

Bellman Equation for MRPs

value function可以分解为两部分：

• 即时奖励$R_{t+1}$
• 后继状态的折扣值$\gamma v(s_{t+1})$
  下一次状态的value function的返回值
  
  贝尔曼方程的基本思想是对value function进行递归分解。
  为什么即时奖励索引为t+1？
  这只是一种表示方式，也可以不这么表示。这种表示方式的理由是：考虑了environment和agent之间的界限，它的思想是，我们采取action进入环境后，然后一个时间步就产生了，环境发生改变后，因为下标是在控制环境传递回来的时间步，所以说是新时间步。环境发生改变之后，任何东西的下标都会变成t+1。

Bellman Equation for MRPs（2）

Example: Bellman Equation for Student MRP

Bellman Equation in Matrix Form（矩阵形式的Bellman方程）

Bellman方程可使用矩阵简明表示
$v=R+\gamma Pv$
其中v是一个列向量，每个状态一个条目

Solving the Bellman Equation(求解Bellman方程)

• 贝尔曼方程是线性方程
• 可以直接解决：
  
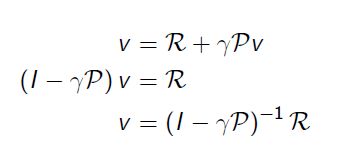
• 对于n个状态，计算复杂度为$O(n^3)$
• 直接求解仅适用于小型MRP
• 对于大型MRP，有很多迭代方法，例如：
  • Dynamic programming（动态编程）
  • Monte-Carlo evaluation（蒙特卡洛评估）
  • Temporal-Di↵erence learning（时差学习）

三、Markov Decision Process

（一）定义

马尔可夫决策过程（MDP）是具有决策的马尔可夫奖励过程（MRP）。 它在所有状态具有马尔可夫性质的环境中。

S，A是有限集合
状态转移矩阵依赖于action
R可能依赖于action，也可能不依赖与action。通常情况下以来与action

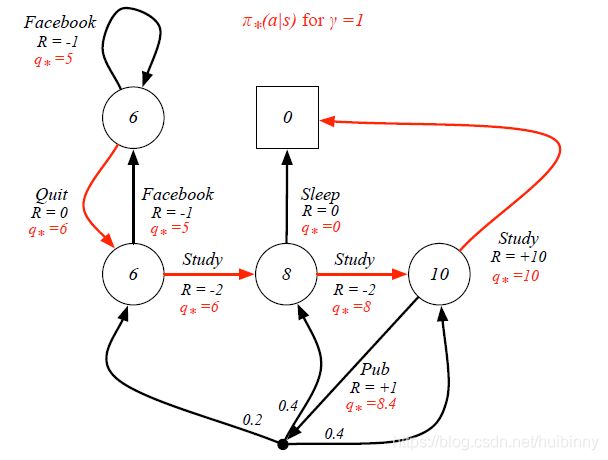
（二）Example: Student MDP

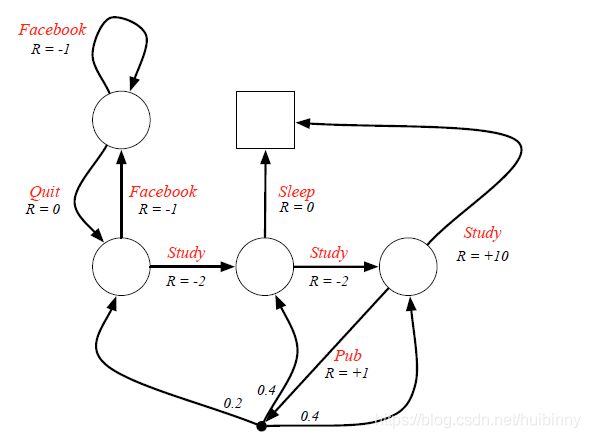
红色为各种action。
对于要走的路径，现在有了更多的控制权
现在的目标是：在决策过程中，找到最佳的一条路径，这条路径最大化的得到的reward

（三）Policies（1）

如何形式化做决策这件事，引入policy

policy实际上是一个状态转移矩阵。
现在讨论的是随机policy（随机这个概念是有用的，它使得我们可以进行探索），这些policy是在给定state的情况下，一个关于actions的概率分布，这个分布会给你一个映射，这个分布会告诉你，如果我处于这个state，这个映射反映的就是往左走的概率或往右走的概率。

• 策略完全定义了agent的行为
• MDP策略取决于当前状态（而不是历史记录）
• 即政策是静态的（与时间无关）
  $A_t\sim \pi (\cdot |S_t),\forall t>0$
  • 静态policy：不顾我们在哪个时间步到达这个状态，我们所采取的措施是一样的，policy所依赖的唯一一个因素是我们当前所处的state，跟时间无关。这对优化过程来说是很有效的，但根据定义来看，我们现在具有Markov Property，所以一个state就能特征化接下来所有会发生的事情。

为什么没有reward？

• 因为state s已经完全囊括了你未来的reward，在MRP、MDP中，Markov Property意味着state s完全特征化了从这个state开始以后的演化过程，所以你需要找的是给定state之后的policy，你想要找到一个能够最大化未来reward的action，我们需要查看我们当前所处的state，然后决定我们下一步采取的action，reward是未来的，我们不在乎过去得到了多少reward。

（四）Policies (2)

我们可以把一个MDP还原为MRP或MP，我们要抽取一些states序列，当我们遵循一个特定的流程，抽取得到一个states序列时，这个序列实际上就是一个Markov chain。不管我们选择了一个什么样的policy，我们选择的那个policy来找到对应的Markov chain，这实际上就定义了我们的动态过程。
如果我们一旦固定这个policy，之研究这个states序列和reward，再走一遍这个过程，这是一个MRP。

（五）Value Function

MDP的状态值函数$v_{\pi }(s)$是从状态s开始，然后遵循策略$\pi$的预期收益。
如果选择policy$\pi$，state s有多好，能得到多少reward

告诉我们在一个特定的状态，采取一个特定的action有多好，总的reward是多少。
action肯呢个会影响immediate reward和结束时所处的state，采取action可能是有成本的，不同的action和不同的成本联系，并带到不同的state。

Example: State-Value Function for Student MDP

（六）Bellman Expectation Equation（贝尔曼期望方程）

state-value function(状态值函数)可以再次分解为即时reward加上后继状态的discounted value

action-value function(动作值函数)可以类似地分解:

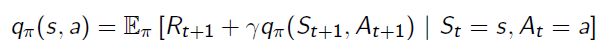
如果我在某一状态下，采取一个action，然后我会得到一些immediate reward（这个reward是给特定的action的）然后我看看我在哪里结束，我可以看看我结束的state的action value，从该起点跟随policy采取特定的action。

Bellman Expectation Equation for $V_{\pi }$

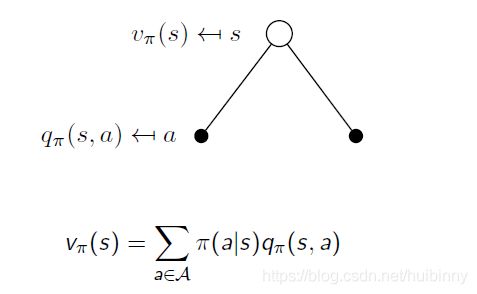
有一定概率向左走或向右走，由policy决定，qvalue告诉我们从这个state采取这一action有多好。
对这些q value求平均，得到$v_{\pi }(s)$在那个state下value是多少。

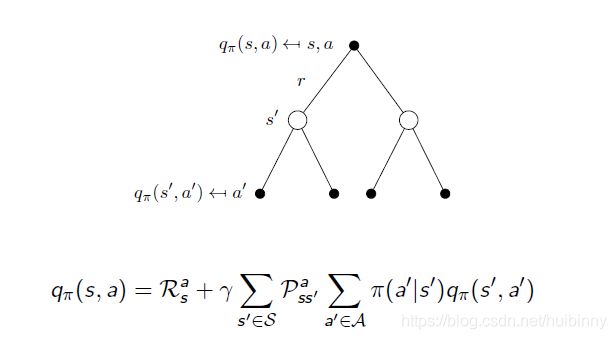
Bellman Expectation Equation for $Q_{\pi }$

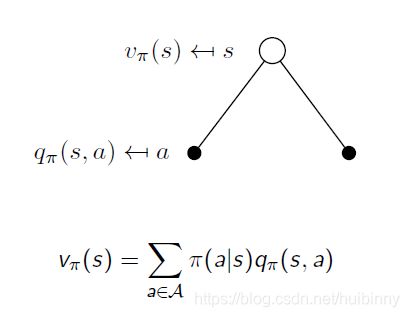
这棵树根部是一个state，我们在考虑这个特殊的state，从这个state向右走会有多好，我们呢必须把这些动态MDP求均值。
采取action a导致环境变化的可能状态有多种。

Bellman Expectation Equation for $V_{\pi }$（2）

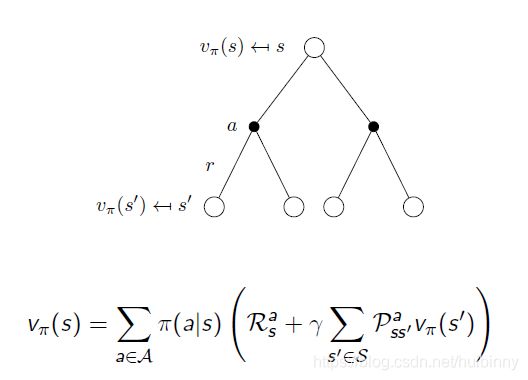
一个状态下可能执行多个不同的action，执行一个action也可能导致不同的环境变化，进而引起状态的变化。

Bellman Expectation Equation for $Q_{\pi }$（2）

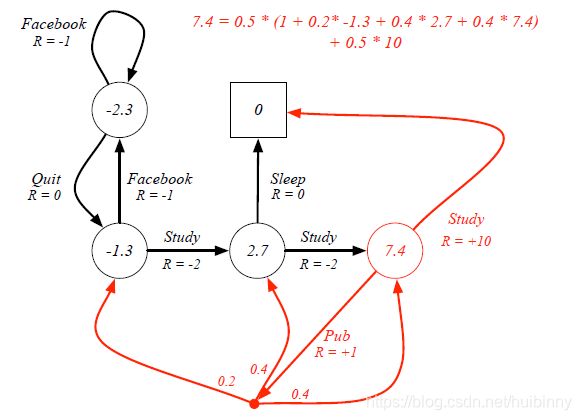
Example: Bellman Expectation Equation in Student MDP

Bellman Expectation Equation (Matrix Form)

Bellman期望方程可以使用归纳MRP简洁表达：

$R^{\pi }$,$P^{\pi }$都为平均值

（七）Optimal Value Function

我们真的不关心在马尔科夫链中我们可以获得多少rewards，我们关心的是再系统中找到最佳路径。一般来说，你要找到最优的方法来解决你的问题。

• 最佳值函数指定MDP中可能的最佳性能。
  我们可以通过马尔科夫链得到很多不同的policy，我们所关心的是这些policy中最好的。用不同的方式遍历系统，每一个不同的policy将导致不同的进化，我们关心那个policy可以带来期望中的最多的reward的，$V_{\ast }$没有告诉你最好的policy是什么，它告诉了你什么时最大可能的reward。
• 当我们知道最优值fn时，“已解决MDP”。
  在所有给定的policy和所有可能采取的action能得到最大reward。在所有不同的方法下，如果你向左走，你可能会得到17的单位的奖励，如果向右走，你可以得到80个单位的奖励，你会选择往右走，这马上告诉你采取向右走的action。如果你有$q_{\ast }$，你就完成了要做的事情。

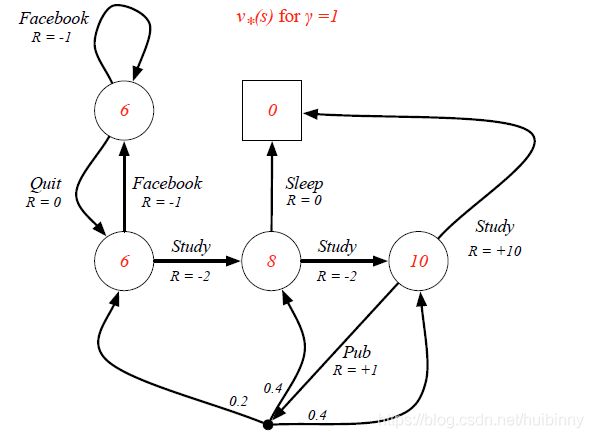
Example: Optimal Value Function for Student MDP

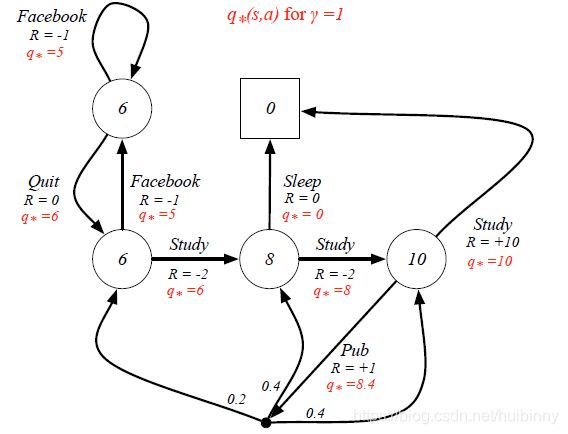
Example: Optimal Action-Value Function for Student MDP

Optimal Policy

定义一个基于policy的部分排序

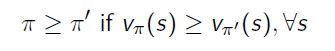
如果一个policy的value function大于另一个，则这个policy比另一个好。

定理：

至少存在一个最好的policy
可以有不止一个最优policy，多个最优policy必须达到相同数量的reward，例子：在你的MDP里有两个不同的action，可以带你到相同的state，对于你采取那个action其实无所谓，他们都可以是最优。

Finding an Optimal Policy

可以通过最大化$q_{\ast }(s,a)$来找到最佳策略.

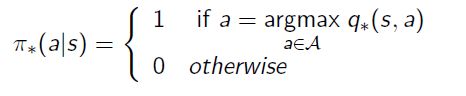
• 任何MDP始终都有确定性的最佳策略
• 如果我们知道$q_{\ast }(s,a)$，我们将立即获得最优策略

Example: Optimal Policy for Student MDP

红线是最优的action。

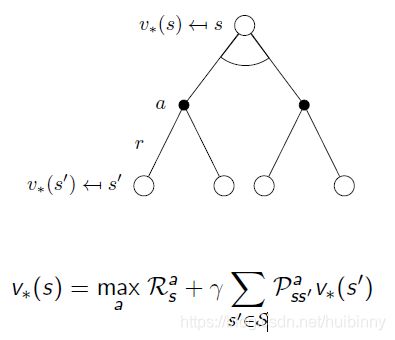
Bellman Optimality Equation（贝尔曼最优方程） for $V_{\ast }$

最佳值函数通过Bellman最优方程递归相关：

向前看一步，每个action对应的q值，计算这些值得最大值，而不是求平均。然后可以评估 $V_{\ast }(s)$有多好。

Bellman Optimality Equation（贝尔曼最优方程） for $Q_{\ast }$

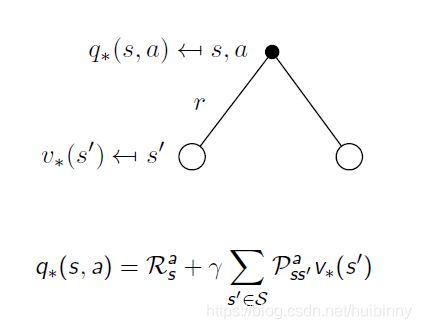
采取一个特定action的最优value是多少?
方法：
第一步：向前看一步，采取一个action可能到达多个state
第二步：每个state都会有一个最优value值
第三步：求多个state的value的平均值。

Bellman Optimality Equation（贝尔曼最优方程） for $V_{\ast }$（2）

Bellman Optimality Equation（贝尔曼最优方程） for $Q_{\ast }$（2）

Example: Bellman Optimality Equation in Student MDP

Solving the Bellman Optimality Equation（求解Bellman最优方程）

• 贝尔曼最优方程是非线性的
• 没有封闭式解决方案（通常）
• 许多迭代求解方法
  • Value Iteration
  • Policy Iteration
  • Q-learning
  • Sarsa

理解贝尔曼方程：
例子：Atari 游戏
当我们得到 $Q_{\ast }$或 $V_{\ast }$时，它会告诉你，你能得到的最大值是多少，假设你处于这个屏幕，你可以从这个屏幕的多少分，我们的直觉是，你需要做的唯一一件事就是得到最高分，这就是作为的最优原则。最优原则会告诉你获得最高分的方法是，在上一个状态尽力表现争取最大值，在接下来的轨迹中也要尽力去获得最大值，如果这样做了，骑士你就获得了结束状态的value function，所以你现在需要做的就是如何在上一个状态上去获得最大值，你去求得最大值的方式就是去最大化你有可能结束的那些状态的最优value function，贝尔曼方程的直觉就是把自己未来的轨迹分成两部分，分为当前最优决策和之后的最优决策，你可以在贝尔曼方程的帮助下，去描述最优的动态是什么。

如何表示一个大的MDP？
reward function是由动态环境给出的，例如Atari，有超过一百万个state，分数是关于state的一个函数，你处在这个state，然后你推出游戏模拟器，分数会在屏幕上显示。这只是一个依赖于所处state的函数。reward function是state和reward的一个映射，这个函数会特征化。
对于任何合理的问题，都有一个办法将问题进行转换。

四、Extension to MDPs

• 无限和连续的MDP
• 部分可观察的MDP
• 无折扣的平均奖励MDP

(一）Infinite MDPs（无限MDP）

以下扩展都是可能的：

• 无限的状态和/或动作空间
  • Straightforward
• 连续状态和/或动作空间
  • 线性二次模型（LQR）的封闭形式
• 连续时间
  • 需要偏微分方程
  • 汉密尔顿-雅各比-贝尔曼（HJB）方程
  • Bellman方程的极限情况为$time-step\to 0$

（二）Partially Observable MDPs（部分可观察）

POMDPs

部分可观察的马尔可夫决策过程是具有隐藏状态的MDP。 这是一个带有动作的隐马尔可夫模型。

Belief States

Belief States $b(h)$是状态的概率分布，条件是历史h

Reductions of POMDPs

• 历史$H_t$满足Markov性质
• Belief State$b(H_t)$满足Markov性质
  
• POMDP可以简化为（无限）历史树
• POMDP可以简化为（无限）置信状态树

(三)Average Reward MDPs

Ergodic Markov Process

遍历马尔可夫过程是

• Recurrent：每个状态都被访问了无数次
• Aperiodic(非定期的)：访问每个状态都没有任何系统的周期

遍历马尔可夫过程具有以下性质的极限平稳分布

Ergodic MDP

定义：如果任何策略引起的马尔可夫链都是遍历的，则MDP是遍历的。

对于任何策略$\pi$，遍历MDP的每个时间步长${\rho }^{\pi }$的平均奖励与开始状态无关。

Average Reward Value Function

• undiscounted, ergodic MDP(未打折的遍历MDP)的价值函数可以用平均奖励来表示。
• $v_{\pi }(s)$是从状态s开始的额外奖励，
  
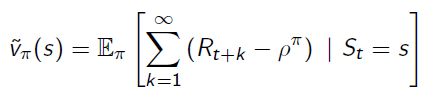
  有一个相应的平均奖励贝尔曼方程
  

Questions?

The only stupid question is the one you were afraid to ask but never did.
唯一愚蠢的问题你不敢提出但从未提出的问题
-Rich Sutton