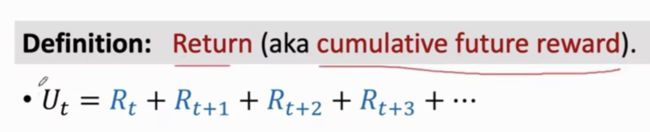【强化学习基础】强化学习的基本概念:状态、动作、智能体、策略、奖励、状态转移、轨迹、回报、价值函数
文章目录
- 1.状态(State)
- 2.动作(Action)
- 3.智能体(Agent)
- 4.策略(Policy)
- 5.奖励(Reward)
- 6.状态转移(State transition)
- 7.智能体与环境交互(Interacts with the environment)
- 8.强化学习随机性的两个来源(Randomness in RL)
-
- 8.1.动作具有随机性(Actions have randomness)
- 8.2.状态转移具有随机性(State transition have randomness)
- 9.轨迹(Trajectory)
- 10.回报(Return)和折扣回报(Discounted return)
- 11.价值函数(Value Function)
-
- 11.1.动作价值函数(Action-Value Function)
- 11.2.状态价值函数(State-Value Function)
1.状态(State)
超级玛丽游戏中,观测到的这一帧画面就是一个 状态(State)。

2.动作(Action)
3.智能体(Agent)
动作是由谁做的,谁就是 智能体(Agent)。自动驾驶中,汽车就是智能体;机器人控制中,机器人就是智能体;超级玛丽游戏中,玛丽就是智能体。
4.策略(Policy)
策略( Policy π \pi π)的含义就是,根据观测到的状态,做出动作的方案, π ( a ∣ s ) \pi(a|s) π(a∣s) 的含义是在状态 s s s 是采取动作 a a a 的概率密度函数PDF。

5.奖励(Reward)
强化学习的目标就是尽可能的获得更多的 奖励(Reward)。

6.状态转移(State transition)
当智能体做出一个动作,状态会发生变化(从旧的状态变成新的状态)。我们就可以说状态发生的转移。状态转移可以是确定的,也可以是随机的。
状态转移函数 p ( s ′ ∣ s , a ) p(s' | s, a) p(s′∣s,a) 的公式:
p ( s ′ ∣ s , a ) = P ( S ′ = s ′ ∣ S = s , A = a ) p(s' | s, a)=\mathbb{P}(S' = s' | S=s, A=a) p(s′∣s,a)=P(S′=s′∣S=s,A=a)
含义为: p ( s ′ ∣ s , a ) p(s' | s, a) p(s′∣s,a) 表示在状态 s s s 时,采取动作 a a a ,跳转到新的状态 s ′ s' s′ 的概率。
7.智能体与环境交互(Interacts with the environment)
步骤一: 智能体观测到环境的状态 s t s_t st,然后做出动作 a t a_t at

步骤二: 由于智能体做出了动作 a t a_t at,环境的状态发生了变化,变成了 s t + 1 s_{t+1} st+1;同时由于智能体做出的动作 a t a_t at, 获得了一个奖励 r t r_t rt。

8.强化学习随机性的两个来源(Randomness in RL)
8.1.动作具有随机性(Actions have randomness)

假定当前状态为 s s s,采取的动作 a a a 具有随机性,可能采取向左的动作,可能采取向右的动作,可能采取向上的动作。
8.2.状态转移具有随机性(State transition have randomness)
假定当前状态为 s s s,采取的动作为 a a a,环境会跳转到下一个状态 s ′ s' s′。状态从 s s s 到 s ′ s' s′ 的转移具有随机性。
9.轨迹(Trajectory)
由状态 s t a t e state state 、动作 a c t i o n action action 、奖励 r e w a r d reward reward 组成的一个序列,成为轨迹(trajectory)。

10.回报(Return)和折扣回报(Discounted return)
回报: 指未来的累计奖励。从t时刻的开始一直到游戏结束,把未来的奖励加起来称之为回报。注意:由于t时刻游戏还没有结束, R t 、 R t + 1 、 R t + 2 R_t、R_{t+1}、R_{t+2} Rt、Rt+1、Rt+2 等奖励, 都是随机变量,不是具体的数值。

折扣率: γ \gamma γ
折扣回报: 带折扣率的回报。
为什么回报具有随机性?
-
1)动作是随机的(状态为 s s s 时,采取的动作 a a a 具有随机性):
P = [ A = a ∣ S = s ] = π ( a ∣ s ) \mathbb{P}=[A=a | S=s] = \pi(a|s) P=[A=a∣S=s]=π(a∣s) -
2)状态转移是随机的(状态 s s s 时采取了动作 a a a ,跳转到下一个状态 s ′ s' s′ ,从状态 s s s 到 状态 s ′ s' s′ 具有随机性):
P = [ S ′ = s ′ ∣ S = s , A = a ] = p ( s ′ ∣ s , a ) \mathbb{P}=[S' = s'| S=s, A=a] =p(s'|s, a) P=[S′=s′∣S=s,A=a]=p(s′∣s,a)
因此,对于任意时刻 i ≥ t i≥t i≥t,奖励 R i R_i Ri 取决于 状态 S i S_i Si 和动作 A i A_i Ai 。
所以,回报 U t U_t Ut 取决于状态 S i 、 S i + 1 、 S i + 2 、 S i + 3 … S_i、S_{i+1}、S_{i+2}、S_{i+3}… Si、Si+1、Si+2、Si+3… 和动作 A i 、 A i + 1 、 A i + 2 、 A i + 3 … A_i、A_{i+1}、A_{i+2}、A_{i+3}… Ai、Ai+1、Ai+2、Ai+3…
11.价值函数(Value Function)
11.1.动作价值函数(Action-Value Function)
如何评估随机变量的好坏? ==> 求期望
动作价值函数: Q π ( s , a ) = E [ U t ∣ S t = s t , A t = a t ] Q_\pi(s,a) = \mathbb{E}[ U_t | S_t = s_t, A_t = a_t ] Qπ(s,a)=E[Ut∣St=st,At=at] ,与状态 S S S 有关,与动作 A A A 有关,同时也与策略 π \pi π 有关。
最优动作价值函数: Q ∗ ( s , a ) = max π Q π ( s , a ) Q^*(s,a) = \max_{\pi}Q_\pi(s,a) Q∗(s,a)=maxπQπ(s,a) , 策略 π \pi π 有无数种,我们要选择一个能让 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a) 最大化的策略 π \pi π。
11.2.状态价值函数(State-Value Function)
状态价值函数: V π ( s t ) = E A [ Q π ( s t , A ) ] V_\pi(s_t) = \mathbb{E}_A[ Q_{\pi}(s_t, A)] Vπ(st)=EA[Qπ(st,A)] ,利用求期望的方式可以把动作 A A A 去掉,因此状态价值函数只与状态 S S S 和策略 π \pi π 有关。