卷积神经网络-高级篇Advanced-CNN

卷积神经网络-高级篇Advanced-CNN

在基础篇中我们学习了一个简单的CNN

下面介绍其他几个网络结构

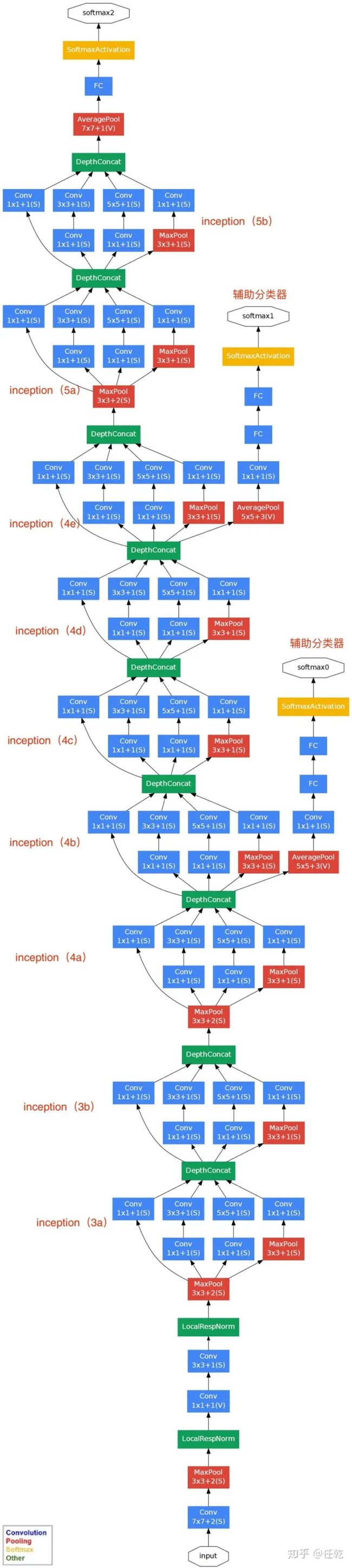
GoogLeNet

蓝色为卷积，红色是池化，黄色是softmax输出，绿色是一些拼接层。

在这个大型的网络结构中我们需要做到的是减少代码冗余（函数、类）

在这个网络结构中有很多相同重复得层，我们可以封装称为一个类

在GoogLeNet中把这样一些层叫做Inception

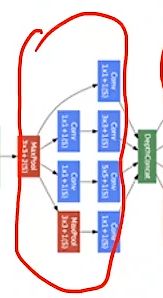
Inception概念

Inception就是把多个卷积或池化操作，放在一起组装成一个网络模块，设计神经网络时以模块为单位去组装整个网络结构。模块如下图所示

在未使用这种方式的网络里，我们一层往往只使用一种操作，比如卷积或者池化，而且卷积操作的卷积核尺寸也是固定大小的。但是，在实际情况下，在不同尺度的图片里，需要不同大小的卷积核，这样才能使性能最好，或者或，对于同一张图片，不同尺寸的卷积核的表现效果是不一样的，因为他们的感受野不同。所以，我们希望让网络自己去选择，Inception便能够满足这样的需求，一个Inception模块中并列提供多种卷积核的操作，网络在训练的过程中通过调节参数自己去选择使用，同时，由于网络中都需要池化操作，所以此处也把池化层并列加入网络中。

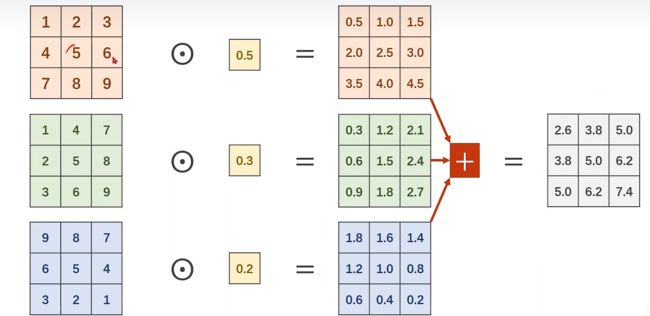
其中Concatenate是把张量拼接在一块，四条路径会产生四个张量，沿着通道拼起来

Average Pooling（平均池化）：可以通过设置padding和stride来保证输入输出的大小是一致的

https://blog.csdn.net/u013289254/article/details/99080916

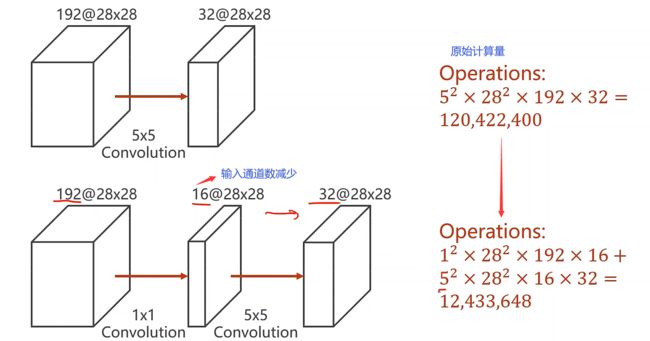
1*1Conv层表示将来的卷积核就是1*1的，他的个数取决于输入张量的通道。

比如有一个3*W*H的图像，通过1*1Conv层都变成1*W*H的feature map

他的作用主要有以下三方面：

1. 跨通道的特征整合
2. 特征通道的升维和降维
3. 减少卷积核参数（简化模型）

https://blog.csdn.net/nefetaria/article/details/107977597

以下图为例，我们可以看到，计算量明显减少。

Inception实现

我们用代码来实现Inception

代码说明：

在池化分支中首先使用average pooling，在对他进行1*1卷积

在1*1分支中直接创建一个1*1的卷积

在5*5分支中有两个模块，第一个是1*1的卷积，第二个模块是5*5的卷积

在3*3分支中包含了三个模块

整体的代码结构如下

最后我们需要把这一整块进行拼接Concatenate

拼接Concatenate代码如下

我们要沿着（B，C，W，H）中dim=1，就是通道的维数拼起来

我们把上面的代码进行整合就可以得到一个Inception类，在这个类中并没有把输入通道写死，说明可以在构造网络中作为参数输入

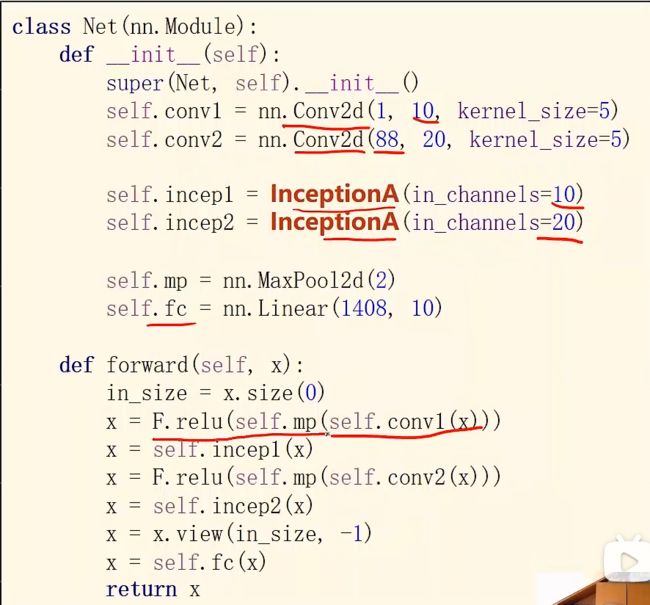
网络模型代码如下：

先是1个卷积层(conv，maxpooling，relu)，然后inceptionA模块(输出的channels是24+16+24+24=88)，接下来又是一个卷积层(conv，maxpooling，relu),然后inceptionA模块，最后一个全连接层(fc)。

1408这个数据可以通过x = x.view(in_size, -1)后调用x.shape得到。

模型实验

我们把这个Inception模型放入Mnist数据集中进行实验

代码演示

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

# prepare dataset

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])  # 归一化，均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


# design model using class

class InceptionA(torch.nn.Module):
    def __init__(self, in_channels):
        super(InceptionA, self).__init__()
        self.branch1x1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)

        self.branch5x5_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)
        self.branch5x5_2 = torch.nn.Conv2d(16, 24, kernel_size=5, padding=2)

        self.branch3x3_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)
        self.branch3x3_2 = torch.nn.Conv2d(16, 24, kernel_size=3, padding=1)
        self.branch3x3_3 = torch.nn.Conv2d(24, 24, kernel_size=3, padding=1)

        self.branch_pool = torch.nn.Conv2d(in_channels, 24, kernel_size=1)

    def forward(self, x):
        branch1x1 = self.branch1x1(x)

        branch5x5 = self.branch5x5_1(x)
        branch5x5 = self.branch5x5_2(branch5x5)

        branch3x3 = self.branch3x3_1(x)
        branch3x3 = self.branch3x3_2(branch3x3)
        branch3x3 = self.branch3x3_3(branch3x3)

        branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
        branch_pool = self.branch_pool(branch_pool)

        outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
        return torch.cat(outputs, dim=1)  # b,c,w,h  c对应的是dim=1


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(88, 20, kernel_size=5)  # 88 = 24x3 + 16

        self.incep1 = InceptionA(in_channels=10)  # 与conv1 中的10对应
        self.incep2 = InceptionA(in_channels=20)  # 与conv2 中的20对应

        self.mp = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(1408, 10)

    def forward(self, x):
        in_size = x.size(0)
        x = F.relu(self.mp(self.conv1(x)))
        x = self.incep1(x)
        x = F.relu(self.mp(self.conv2(x)))
        x = self.incep2(x)
        x = x.view(in_size, -1)
        x = self.fc(x)

        return x


model = Net()

# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)


# training cycle forward, backward, update

def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        # 获得一个批次的数据和标签
        inputs, target = data
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d,%5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # dim = 1 列是第0个维度，行是第1个维度
            total += labels.size(0)
            correct += (predicted == labels).sum().item()  # 张量之间的比较运算
    print('accuracy on test set: %d %% ' % (100 * correct / total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

结果演示

[1,  300] loss: 0.861
[1,  600] loss: 0.222
[1,  900] loss: 0.155
accuracy on test set: 95 % 
[2,  300] loss: 0.115
[2,  600] loss: 0.099
[2,  900] loss: 0.084
accuracy on test set: 97 % 
[3,  300] loss: 0.074
[3,  600] loss: 0.074
[3,  900] loss: 0.073
accuracy on test set: 98 % 
[4,  300] loss: 0.058
[4,  600] loss: 0.062
[4,  900] loss: 0.059
accuracy on test set: 98 % 
[5,  300] loss: 0.050
[5,  600] loss: 0.055
[5,  900] loss: 0.054
accuracy on test set: 98 % 
[6,  300] loss: 0.047
[6,  600] loss: 0.048
[6,  900] loss: 0.046
accuracy on test set: 98 % 
[7,  300] loss: 0.042
[7,  600] loss: 0.043
[7,  900] loss: 0.043
accuracy on test set: 98 % 
[8,  300] loss: 0.039
[8,  600] loss: 0.040
[8,  900] loss: 0.038
accuracy on test set: 98 % 
[9,  300] loss: 0.035
[9,  600] loss: 0.034
[9,  900] loss: 0.038
accuracy on test set: 98 % 
[10,  300] loss: 0.032
[10,  600] loss: 0.032
[10,  900] loss: 0.033
accuracy on test set: 98 % 

结果如下

ResidualNet（ResNet）

随着网络结构的加深，带来了两个问题：

• 一是vanishing/exploding gradient，导致了训练十分难收敛，这类问题能够通过normalized initialization 和intermediate normalization layers解决；
• 另一个是被称为degradation的退化现象。对合适的深度模型继续增加层数，模型准确率会下滑（不是overfit造成），training error和test error都会很高，相应的现象在CIFAR-10和ImageNet都有出现。

https://blog.csdn.net/u011808673/article/details/78836617

残差结构

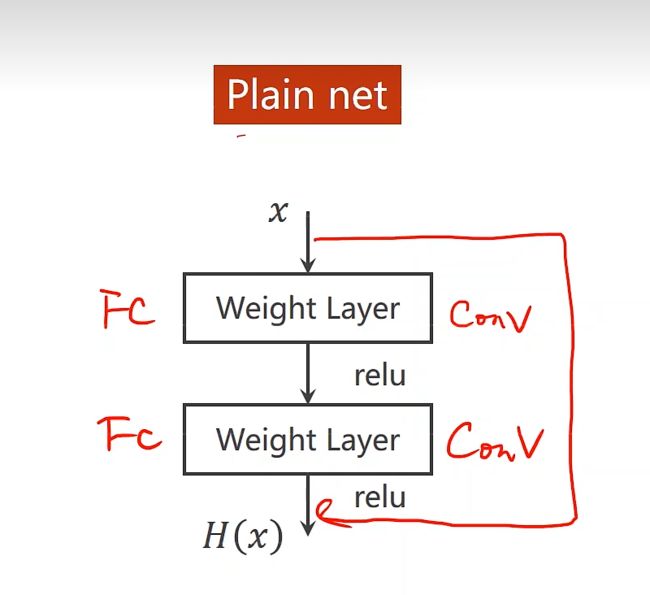
可以看到普通直连的卷积神经网络和 ResNet 的最大区别在于，ResNet 有很多旁路的支线将输入直接连到后面的层，使得后面的层可以直接学习残差，这种结构也被称为 shortcut connections。传统的卷积层或全连接层在信息传递时，或多或少会存在信息丢失、损耗等问题。ResNet 在某种程度上解决了这个问题，通过直接将输入信息绕道传到输出，保护信息的完整性，整个网络则只需要学习输入、输出差别的那一部分，简化学习目标和难度。 同时34层 residual network 取消了最后几层 FC，通过 avg pool 直接接输出通道为1000的 Softmax，使得 ResNet 比16-19层 VGG 的计算量还低。 注意：实现部分是深度未发生变化的连接，虚线部分是深度发生变化的连接。 对应深度有变化的连接有两种解决方案：

1. 使用 zero-pading 进行提升深度 parameter-free。
2. 使用 1*1的卷积核提升维度 有卷积核的运算时间。

两种方法，使用下面一种方法效果更好，但是运行会更耗时，一般还是更倾向于第一种方案节约运算成本。

残差块

在正常的神经网络中就是一层连一层

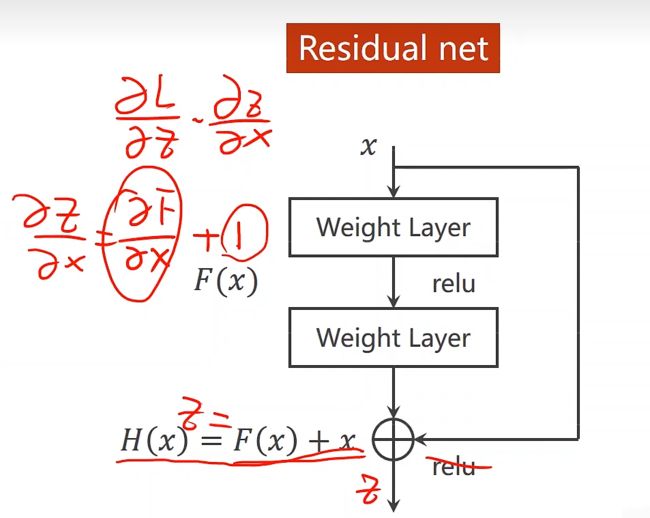
在ResNet中，假定某段神经网络的输入是 x，期望输出是 H(x)，即 H(x) 是期望的复杂潜在映射，但学习难度大；如果我们直接把输入 x 传到输出作为初始结果，通过下图“shortcut connections”，那么此时我们需要学习的目标就是 F(x)=H(x)-x，于是 ResNet 相当于将学习目标改变了，不再是学习一个完整的输出，而是最优解 H(X) 和全等映射 x 的差值，即残差 F(x) = H(x) - x;

ResNet shortcut 没有权值，传递 x 后每个模块只学习残差F(x)，且网络稳定易于学习，同时证明了随着网络深度的增加，性能将逐渐变好。可以推测，当网络层数够深时，优化 Residual Function：F(x)=H(x)−x，易于优化一个复杂的非线性映射 H(x)。

ResNet网络结构

Residual Block 实现

值得注意的是，我们需要输入通道和输出通道一致

第一层中先做卷积在做relu（conv1（x）），第二层中做卷积conv2（y），最后返回relu（x+y）

ResNet代码实现

代码演示

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

# prepare dataset

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])  # 归一化，均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


# design model using class
class ResidualBlock(torch.nn.Module):
    def __init__(self,channels):
        super(ResidualBlock, self).__init__()
        self.channels = channels
        self.conv1 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)
        self.conv2 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)

    def forward(self,x):
        y = F.relu(self.conv1(x))
        y = self.conv2(y)
        return  F.relu(x+y)


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
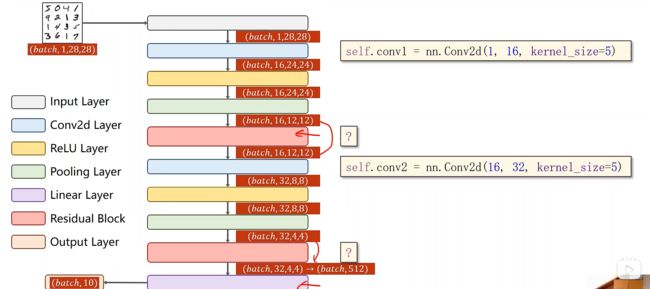
        self.conv1 = torch.nn.Conv2d(1, 16, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(16, 32, kernel_size=5)
        self.mp = torch.nn.MaxPool2d(2)

        self.rBlock1 = ResidualBlock(16)
        self.rBlock2 = ResidualBlock(32)

        self.fc = torch.nn.Linear(512,10)

    def forward(self, x):
        in_size = x.size(0)
        x = self.mp(F.relu(self.conv1(x)))
        x = self.rBlock1(x)
        x = self.mp(F.relu(self.conv2(x)))
        x = self.rBlock2(x)
        x = x.view(in_size, -1)
        x = self.fc(x)
        return x


model = Net()
# 使用GPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)

# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)


# training cycle forward, backward, update

def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        # 获得一个批次的数据和标签
        inputs, target = data
        # 使用GPU
        inputs, target = inputs.to(device), target.to(device)

        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d,%5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 2000))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            # 使用GPU
            images, labels = images.to(device), labels.to(device)
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # dim = 1 列是第0个维度，行是第1个维度
            total += labels.size(0)
            correct += (predicted == labels).sum().item()  # 张量之间的比较运算
    print('accuracy on test set: %d %% [%d/%d]' % (100 * correct / total, correct, total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

输出结果

[1,  300] loss: 0.085
[1,  600] loss: 0.025
[1,  900] loss: 0.018
accuracy on test set: 97 % [9728/10000]
[2,  300] loss: 0.014
[2,  600] loss: 0.013
[2,  900] loss: 0.011
accuracy on test set: 97 % [9781/10000]
[3,  300] loss: 0.009
[3,  600] loss: 0.009
[3,  900] loss: 0.009
accuracy on test set: 98 % [9842/10000]
[4,  300] loss: 0.007
[4,  600] loss: 0.007
[4,  900] loss: 0.007
accuracy on test set: 98 % [9868/10000]
[5,  300] loss: 0.006
[5,  600] loss: 0.006
[5,  900] loss: 0.006
accuracy on test set: 98 % [9898/10000]
[6,  300] loss: 0.006
[6,  600] loss: 0.005
[6,  900] loss: 0.005
accuracy on test set: 98 % [9896/10000]
[7,  300] loss: 0.005
[7,  600] loss: 0.005
[7,  900] loss: 0.005
accuracy on test set: 98 % [9896/10000]
[8,  300] loss: 0.004
[8,  600] loss: 0.004
[8,  900] loss: 0.004
accuracy on test set: 99 % [9906/10000]
[9,  300] loss: 0.004
[9,  600] loss: 0.004
[9,  900] loss: 0.004
accuracy on test set: 99 % [9913/10000]
[10,  300] loss: 0.003
[10,  600] loss: 0.003
[10,  900] loss: 0.004
accuracy on test set: 99 % [9909/10000]