学习自旋电子学的笔记06:“扫参数”批量微磁模拟,ubermag介绍,微磁模拟求助
文章目录
- 前言
- 一、“扫参数”进行批量微磁模拟
-
- 1.“扫参数”的基本技巧
- 2.使用for命令让Boxsi“扫参数”实现批量化运行
- 二、一个非常综合的微磁模拟工具包“ubermag”
-
- 1.“ubermag”的简单介绍
- 2.“ubermag”的使用体验
- 三、微磁模拟求助
- 总结
空山不见人,但闻人语响。——王维《鹿柴》
前言
七月流火,大家的进展如何啊?这个月的总结内容相比以往Blog少了许多,主要原因是在复现一篇别人的文章时遇到了一些困难导致消耗了大量时间去做模拟,结果也是不出意外的出意外了----还是没有复现出来,,,在文末会介绍关于这篇文章的相关信息。本文开篇会介绍一个算不上新奇的技巧,即如何“扫参数”来实现批量并行微磁模拟。接着给大家推荐一个微磁模拟工具包“ubermag”,相信大家在了解这个工具包之后,都会有一种相见恨晚的感觉。一、“扫参数”进行批量微磁模拟
1.“扫参数”的基本技巧
相信大家对“扫频”和“扫场”两个名词都有所耳闻,它们分别表示对外场的频率和幅值进行连续调节,来研究对系统的影响,那么稍微扩展一下这个名词,“扫参数”的意思就是对系统的某个参数进行连续调节,从而研究这个参数对系统的影响。
在进行微磁模拟时,通常我们需要在某个参数的一定取值范围内连续调节这个参数来研究这个参数对研究对象的影响,比如在论文中常见的电流密度、外加磁场的幅值和频率,以及磁性材料的各种参数的变化等等情况,这时会出现对于同一个.mif文件(微磁问题描述文件)的内容,我们需要手动的连续多次修改文件中的一个参数,然后手动的打开多个Oxsii求解器并分别加载修改后的.mif文件,最后手动的点击运行。比如电流密度的大致范围是1e11到1000e11A/m2,在寻找使磁化翻转的精确电流密度阈值时,这时就需要在.mif文件中以1e11A/m2的步长连续调节电流密度,如此操作便需要手动修改并生成1000个.mif文件然后运行,显然我们可以使用批处理命令来自动实现这一流程。
那么在“扫参数”前应该做哪些准备工作呢?
①首先我们可以按照自己的代码风格编写一个微磁模型尺寸正确的,能量项无误的.mif文件,即使用Oxsii求解器来加载并运行此文件,通过Oxsii方便的手动交互式输出来检验这个基本的.mif文件是否满足以上要求。
②有了这个基本的.mif文件之后,之后才应该根据自己的需求去关联.mif文件中变化的参数。通常“扫参数”大致分为三种场景:改变磁体系的模型尺寸,改变材料的磁性参数,改变外加磁场(电流)的参数。对于一些需要自动变化的参数,特别是一些关联了模型尺寸的参数,比如各种空间不均匀的标量场和矢量场,这就需要在.mif文件中使用与参数关联的函数或者表达式来为它们赋值,而不是使用一些固定的数值为它们赋值,这样在“扫参数”时,真正做到 “牵一发而动全身” 的效果。
③在仔细关联好各种参数之后,就可以避免重复模拟相同的参数来浪费时间了。接着就可以用Parameter命令来定义需要被扫的参数了。
④最后,“扫参数”应按照从大到小的变化步长来细化模拟中的参数范围。先迈开“大步子”确定参数的大致范围之后,再从这个大致范围中迈出“小步子”,减少步长来精细化模拟。
2.使用for命令让Boxsi“扫参数”实现批量化运行
在前文笔记3,4,5中已经多次用到过批处理命令了,比如批量比较磁化文件之间的差异,批量转换矢量场文件的数据格式等,无非就是通过批处理命令结合OOMMF的命令行工具实现批量重复的操作而已。但是在前文中没有提到过Boxsi求解器,因此在这里补充一下其用法,通过OOMMF文档的第7.2节可知,相比Oxsii求解器而言,Boxsi更适合作为批量求解器。根据文档中Boxsi的相关参数,不难实现一个“扫参数”批量微磁模拟的代码框架如下:
@ rem 请将该批处理文件放在oommf安装根目录
@ rem 开启变量延迟
@ setlocal enabledelayedexpansion
@ rem 待运行的mif文件
@ set mif_file=D:\mif_run_dir\edge_mode_SW\relax#Hy@1e3Oe\relax#[email protected]
@ rem boxsi运行时的输出目录
@ set out_directory=D:\mif_run_dir\edge_mode_SW\relax#Hy@1e3Oe\
@ rem 定义一些字符串变量,方便后面拼接字符串
@ set symbol_at=@
@ set symbol_space=
@ set symbol_bracket_start="
@ set symbol_bracket_end="
@ rem “扫参数”的相关设置
@ set sweep_parameter_lable=xcell
@ set sweep_parameter_start=5
@ set sweep_parameter_step=-1
@ set sweep_parameter_end=2
@ rem 以下命令是使用boxsi的命令,请先理解它的命令参数
@ rem "md 文件夹名":表示创建一个文件夹
for /l %%p in (%sweep_parameter_start%,%sweep_parameter_step%,%sweep_parameter_end%) do (
@ set sweep_parameter=%%p
@ set sweep_parameter_directory=%out_directory%%sweep_parameter_lable%%symbol_at%!sweep_parameter!
@ md !sweep_parameter_directory!
@ set sweep_parameter_lableValue=%symbol_bracket_start%%sweep_parameter_lable%%symbol_space%!sweep_parameter!%symbol_bracket_end%
@ start /min cmd /c "tclsh oommf.tcl boxsi -outdir !sweep_parameter_directory! -parameters !sweep_parameter_lableValue! %mif_file%"
@ echo "boxsi已开始运行"%mif_file%",当前“扫参数”为:"!sweep_parameter_lableValue!
)
“扫参数”过程中,每一个参数对应的新建输出文件夹被命名为“参数名@参数值”的风格。不过此处设计为只有一个参数可以被扫,大家可以按自己需求做额外参数的补充,无非就是每多一个参数就多一个嵌套的for命令,推荐大家使用“#”来分割文件夹名称中的不同参数项,即使用“参数名1@参数值1#参数名2@参数值2#参数名3@参数值3”的风格来命名输出文件夹。
对于以上框架的内容,这里还是稍微解释一下两个地方:
① for /l %%p in (start,step,end): for命令后面的参数 /l 表示在数值start到end范围内,使参数%%p进行步长为step的迭代,这其实就达到了其他语言中的for循环的效果。
②start /min cmd /c :首先start /min表示 无阻塞的并行启动 一个程序,并使其窗口最小化,后面的cmd /c表示在Windows命令行程序“CMD”中执行完cmd /c尾随的命令后,自动关闭该命令行程序“CMD”的窗口。
二、一个非常综合的微磁模拟工具包“ubermag”
1.“ubermag”的简单介绍
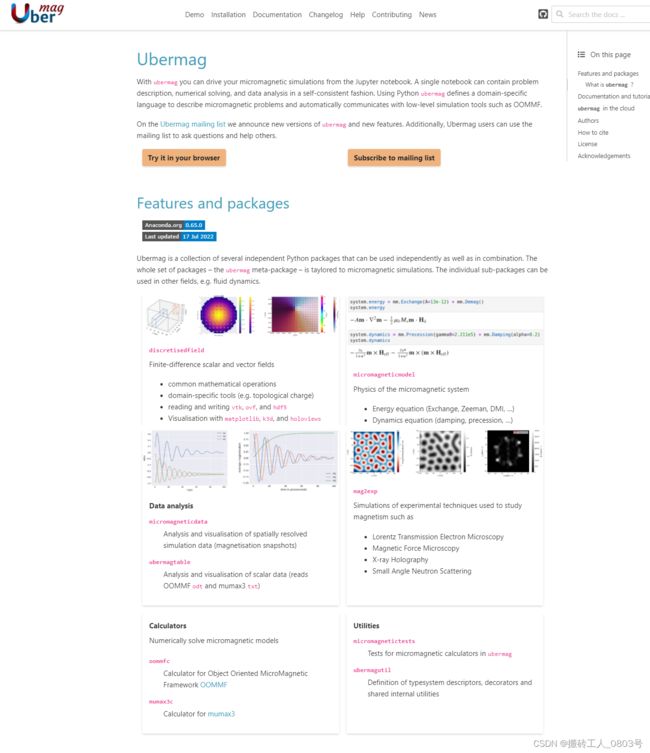
目前使用有限差分法(FDM)的主流微磁模拟程序包有:基于CPU运算的OOMMF,基于GPU运算的mumax3。关于微磁问题描述文件的编写,前者的.mif文件使用的语法是Tcl语言+OOMMF特有的命令和类,而后者的.mx3文件使用的语法是Go语言+mumax3特有的命令,两者各自特有的关键字和类不尽相同。对于部分人来说,会觉得完全不值得耗费精力把这两种程序包的语法都学会,那么在此给大家推荐一个非常综合的微磁模拟工具包“ubermag”,无论是已经掌握OOMMF和mumax3等微磁模拟程序的资深人士还是啥模拟程序都没学过的刚入门的小白,都值得上手体验一波。
之所以将“ubermag”叫做微磁模拟工具包而不是微磁模拟程序包,正如“ubermag”的名字那样,它自身并没有计算引擎,而是基于集成了其它现有的计算引擎作为计算后端的基础上,面向用户提供了更加简单的微磁问题描述文件的编写方式。到目前为止,这个工具包同时集成了OOMMF和mumax3作为计算后端,而“ubermag”作为前端来面向用户并与之交互,它屏蔽了OOMMF和mumax3的语法差异,取而代之的是使用Python语言+“ubermag”特有的类来编写微磁问题描述文件,当用户按照规范的“ubermag”语法来编写微磁问题描述文件(即.py文件)后,ubermag就会根据这个文件来生成OOMMF所需的.mif文件或者mumax3所需的.mx3文件,从而有了 “一份代码,到处运行” 的效果。而且由于用户采用的是Python语言来编写微磁问题描述文件,结合另一个工具包Jupyter lab,这极大的扩展了用户与微磁模型的交互方式,对微磁数据的后处理也会更加得心应手。
大家看看ubermag官网的首页,是不是感觉这个工具包十分高端大气上档次呢?
而且ubermag官网上的各种文档都是非常齐全,非常详细的,包含ubermag的安装指南,API使用文档,各种示例文档,微磁学相关能量项的解释等等。ubermag社区里面还有一份推导微磁学各种公式的笔记,无法去外网下载的用户,可以点击此处下载,里面包含了交换能,各向异性能,界面/体DMI能等能量项的推导过程,以及这些能量相互竞争导致对一维的布洛赫和奈尔型畴壁和二维的布洛赫和奈尔型斯格明子的影响,要彻底理解该笔记的内容,需要一定的矢量分析和变分法等数学知识。
如果大家在使用ubermag的过程中遇到了问题,可以去ubermag社区的帮助板块里面看看,里面有许多用户提出的问题和相关的解决方法。
2.“ubermag”的使用体验
“ubermag”的安装过程见官网,这里总结一下本人自己的安装和测试流程吧:
①下载并安装Python的包管理器Miniconda,安装结束后在Windows的开始菜单中会出现两个新的命令行程序:Anaconda Powershell Prompt (Miniconda3)和Anaconda Prompt (Miniconda3),虽然这两个命令行程序打开后外观显示都差不多,但是请往后看,了解两者为什么 不能混淆使用 。
②如官方文档所述,用户需要单独为ubermag创建一个虚拟的运行环境,即在Anaconda Prompt (Miniconda3)命令行中依次输入以下两条命令:
conda create -n ubermag_env python=3.8
conda activate ubermag
③接着是从代码仓库中抓取ubermag工具包的代码,即在上一步骤输入的命令执行完成之后,再输入以下命令:
conda install --channel conda-forge ubermag
④等待ubermag工具包的所有代码下载结束后,在上一步骤输入的命令执行完成之后,再输入以下命令对ubermag进行测试检验:
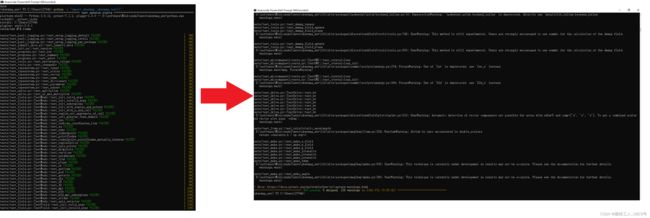
python -c "import ubermag; ubermag.test()"
整个测试检验过程大约半个小时,如下图:
在对ubermag测试结束无错误后,就可以关闭Anaconda Prompt (Miniconda3)命令行程序了,接下来我们就可以正常使用ubermag了。
众所周知,Python是解释型语言,而不是编译型语言,这意味着Python写一段代码就可以运行这一段代码,而不需要提前对整个.py文件进行编译。所以在某种程度上,对于小型的程序来说,使用笔记本类的代码编辑器来编写Python代码反而比IDE好用多了,特别是Jupyter lab这种编辑器,里面可以插入图片,插入公式等内容,无论是对自己编辑代码还是别人阅读代码都十分直观,这是其它类型的代码编辑器无法做到的。
Jupyter lab作为ubermag包中的discretisedfield的依赖包,在上一步骤安装ubermag的时候就自动下载好了,要启动Jupyter lab代码编辑器,只需在 Anaconda Powershell Prompt (Miniconda3) 中依次输入以下两条命令:
conda activate ubermag_env
jupyter lab
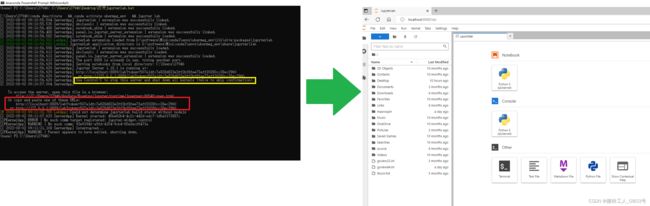
当然,为了以后能方便打开代码编辑器Jupyter lab,可以将这两条命令放入一个.bat文件中,保存在桌面上,然后需要打开时,直接用鼠标把这个文件拖进Anaconda Powershell Prompt (Miniconda3)窗口中就行了:
正如左图黄框中所述,在Anaconda Powershell Prompt (Miniconda3)窗口中使用“Ctrl + C”可以停止运行Jupyter lab。
正如左图红框中所述,若Jupyter lab正在运行中,可以在浏览器中输入这个本地网址从而打开右图的这个界面。
至于Jupyter lab代码编辑器的使用就没啥可讲的了,接下来会介绍一个切换mumax3作为计算后端时遇到的问题(oommf程序包是绑定在ubermag工具包里面被一起下载的,并作为默认的计算后端),正如ubermag社区中描述的问题那样,即使用户将mumax3的全路径添加进了系统的环境变量Path中,仍然会出现以下报错内容表示找不到mumax3的路径:
OSError: Mumax3 cannot be found. Mumax3 does not come automatically with Ubermag. Make sure it is properly installed and can be found on the command line.
其中有一个解决方法是在import mumax3c as mc语句的下面补充一条语句,显式的指定文件mumax3.exe的全路径,如下所示:
import mumax3c as mc # Micromagnetic Calculator
mc.runner.runner = mc.mumax3.ExeMumax3Runner(mumax3_exe='D:\\software\\微磁模拟\\mumax3\\mumax3.exe')
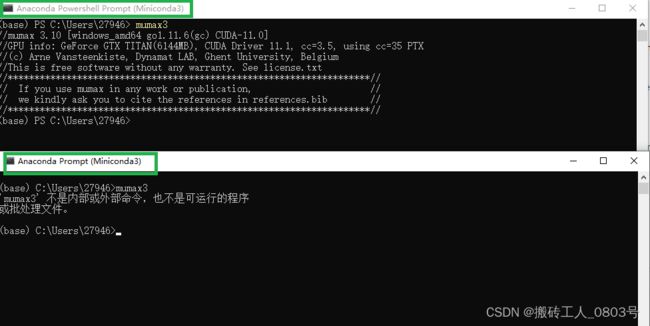
其实这是由于在ubermag的虚拟环境中没有识别到系统的环境变量导致的,对比分别在Anaconda Powershell Prompt (Miniconda3)和Anaconda Prompt (Miniconda3)窗口中输入mumax3,如下图:
显然只有Anaconda Powershell Prompt (Miniconda3)能识别到环境变量,这就是要在Anaconda Powershell Prompt (Miniconda3)中打开Jupyter lab代码编辑器的原因,因此不要混淆使用Anaconda Powershell Prompt (Miniconda3)和Anaconda Prompt (Miniconda3)。
三、微磁模拟求助
俗话说:赠人玫瑰,手留余香!如果有人看到了这里,并且您有基本的微磁模拟相关能力的话,并且最近有闲暇时间的话,请看完以下的微磁模拟求助信息。
硕士论文《自旋波逻辑器件的关键技术研究》,以及它的小论文《Bias-free reconfigurable magnonic phase shifter based on a spin-current controlled ferromagnetic resonator》(DOI:10.1088/1361-6463/ab5c81),我需要复现的是小论文的Figure 2.( c)、(d),Figure 3.(a)、(d)、(e),Figure 5.(b)总共6张图。
这里就不把图片放出来了,有兴趣的大佬可以去看一下原文,下面给出我的模拟结果:
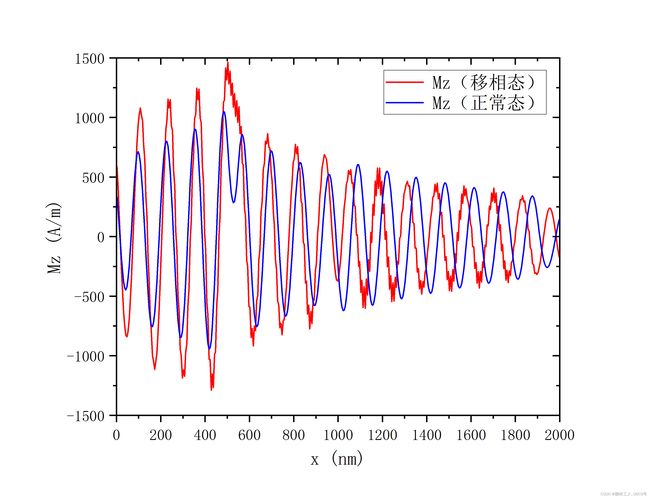
Figure 2.( c)表示对比正常态和移相态在10ns时刻,沿着波导的x方向磁化分量Mz的空间域分布:
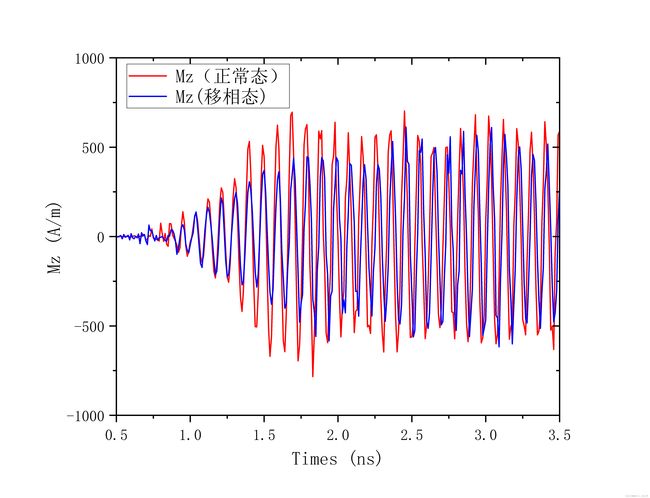
Figure 2.(d)表示对比正常态和移相态在波导x=1300 nm处,磁化分量Mz在0.5至3.5 ns内的时域分布:
Figure 3.(a)表示谐振器的动态偶极杂散场分布。这个完全不会,,,不过我有一个思路不晓得对不对:
①原有的微磁模型占据的容器尺寸为2000 X 150 X8nm,现在将原有的磁体系放入在容器尺寸为2000 X 300 X16nm的正中心,没有占据的单元格按无磁性处理。将原有5 X 5 X 2nm的网格尺寸改为5 X 5 X 1nm。
②在没有谐振体(即谐振体区域的Ms为0)的作用时,并且10.5GHz自旋波在波导中传播时,每1ps就保存一次Oxs_Demag-Field输出项,模拟总共运行200ps。
③在有谐振体(且谐振体的磁化方向指向-y)的作用时,并且10.5GHz自旋波在波导中传播时,每1ps就保存一次Oxs_Demag-Field输出项,模拟总共运行200ps。
④将第三步获取的矢量文件减去第二步获取的在时间上一一对应的矢量文件,从而可以得到200个差值文件,我个人觉得这应该就是动态偶极杂散场,,,了吧?
下图是通过以上方式获取的谐振体区域的“动态偶极杂散场”:
Figure 3.(d)表示正常态时,谐振体在2ns到2.09ns内磁化状态,其中颜色表示Mz的大小:
Figure 3.(e)表示移相态时,谐振体在2ns到2.09ns内磁化状态,其中颜色表示Mz的大小:
Figure 5.(b)表示在不同的电流密度改变谐振体的磁化状态(SOT效应)的情况下,在波导的x=1300nm处,获取自旋波在9.8到10ns时间内的时域分布:
由于并没有把这篇文章复现出来,所以这里就不张贴代码了,如果有大佬复现成功了,请务必私信或者评论区分享一下经验,如果您的结果和我的差不多,也请私信或者评论区分享一下,我们可以相互交流一下找找出错的原因。