《PyTorch深度学习实践》自学记录 第七讲 处理多维特征的输入
B站 刘二大人 ,传送门PyTorch深度学习实践——处理多维特征的输入![]() https://www.bilibili.com/video/BV1Y7411d7Ys?p=7&vd_source=7f566d315de0869cb5d989e64824dcbd
https://www.bilibili.com/video/BV1Y7411d7Ys?p=7&vd_source=7f566d315de0869cb5d989e64824dcbd
参考错错莫课代表的PyTorch *深度学习实践 第7讲*![]() https://blog.csdn.net/bit452/article/details/109682078
https://blog.csdn.net/bit452/article/details/109682078
笔记(视频截图):
之前的学习,我们学会了对一位特征输入进行处理,本节介绍了如何处理多维特征输入。
多维特征输入就需要每一个维度的x乘相应的权值w的和加上一个偏置量b,送入sigmoid函数进行二分类.
下载好数据集之后我们要构建网络计算图,从八维到一维共三层:第一层是8维到6维的非线性空间变换,第二层是6维到4维的非线性空间变换,第三层是4维到1维的非线性空间变换。
按理说层数是自己去设定的,层数越多,最终得到的模型可能效果越好,但值得注意的是,我们不能一味去追寻学习能力,因为过度的学习会将不需要的噪音也学习到,而噪音在实际中是随机的,所以说要提升我们算法模型的泛化能力。
源代码如下:
import numpy as np import torch import matplotlib.pyplot as plt # prepare dataset xy = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32) x_data = torch.from_numpy(xy[:, :-1]) # 第一个‘:’是指读取所有行,第二个‘:’是指从第一列开始,最后一列不要 y_data = torch.from_numpy(xy[:, [-1]]) # [-1] 最后得到的是个矩阵 # design model using class class Model(torch.nn.Module): def __init__(self): super(Model, self).__init__() self.linear1 = torch.nn.Linear(8, 6) self.linear2 = torch.nn.Linear(6, 4) self.linear3 = torch.nn.Linear(4, 1) self.activate = torch.nn.Sigmoid() # 将其看作是网络的激活层,不单是函数 self.sigmoid = torch.nn.Sigmoid() # 便于调试不同激活函数 def forward(self, x): x = self.activate(self.linear1(x)) x = self.activate(self.linear2(x)) x = self.activate(self.linear3(x)) return x model = Model() # construct loss and optimizer # 默认情况下,loss会基于element平均,如果size_average=False的话,loss会被累加。 criterion = torch.nn.BCELoss(size_average='mean') optimizer = torch.optim.SGD(model.parameters(), lr=0.1) loss_list=[] epoch_list=[] # training cycle forward, backward, update for epoch in range(100): y_pred = model(x_data) loss = criterion(y_pred, y_data) print(epoch, loss.item()) optimizer.zero_grad() loss.backward() optimizer.step() loss_list.append(loss.item()) epoch_list.append(epoch) plt.plot(epoch_list,loss_list) plt.xlabel('epoch') plt.ylabel('cost') plt.show()
部分输出结果:
0 0.7484310269355774
1 0.7369999289512634
2 0.7268263697624207...
998 0.6440109014511108
999 0.6440092325210571
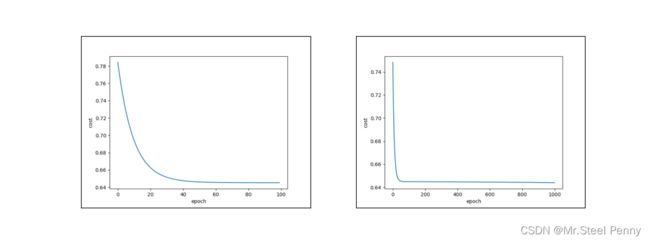
可视化效果:
分别是100次和1000次训练的效果
作业
使用不同激活函数(以Relu为例)
修改代码如下:
class Model(torch.nn.Module): def __init__(self): super(Model, self).__init__() self.linear1 = torch.nn.Linear(8, 6) self.linear2 = torch.nn.Linear(6, 4) self.linear3 = torch.nn.Linear(4, 1) self.activate = torch.nn.ReLU() # 将其看作是网络的激活层,不单是函数 self.sigmoid = torch.nn.Sigmoid() # 便于调试不同激活函数 def forward(self, x): x = self.activate(self.linear1(x)) x = self.activate(self.linear2(x)) x = self.sigmoid(self.linear3(x)) return x
发现ReLU作为激活函数效果要优于sigmoid
可视化效果:
想要查询不同层训练的参数结果,可以用以下代码
layer1_weight = model.linear1.weight.data layer1_bias = model.linear1.bias.data print("layer1_weight", layer1_weight) print("layer1_weight.shape", layer1_weight.shape) print("layer1_bias", layer1_bias) print("layer1_bias.shape", layer1_bias.shape)
ReLU输出结果
layer1_weight tensor
([[ 0.2356, -0.1352, -0.0183, 0.0658, 0.0455, -0.0447, 0.1511, -0.3455],
[ 0.2502, 1.0538, 0.0815, 0.0409, 0.0736, 0.6169, 0.2711, -0.2864],
[ 0.3174, -0.0265, 0.0488, -0.2160, -0.1974, -0.3026, 0.3972, 0.1656],
[-0.1203, -0.5546, 0.3052, -0.2091, -0.1776, -0.6289, -0.4244, -0.5209],
[ 0.3529, -0.3202, 0.0952, 0.1521, -0.1425, -0.0618, 0.3113, 0.0441],
[ 0.0666, -0.2283, 0.1030, 0.1746, 0.1792, 0.2001, 0.2396, 0.2563]])
layer1_weight.shape torch.Size([6, 8])
layer1_bias tensor([-0.3495, 0.5493, -0.0610, -0.2568, -0.2815, 0.2016])
layer1_bias.shape torch.Size([6])
layer2_weight tensor([[-0.2752, -1.0596, -0.2853, 0.8818, -0.2143, -0.1851],
[ 0.3950, 0.3152, 0.1579, -0.4310, -0.3323, -0.3955],
[ 0.0537, 0.4864, 0.3449, -0.1965, 0.1226, 0.2554],
[ 0.2260, -0.6714, 0.2942, 0.2321, 0.3767, -0.0583]])
layer2_weight.shape torch.Size([4, 6])
layer2_bias tensor([1.1316, 0.5149, 0.2538, 0.6514])
layer2_bias.shape torch.Size([4])
layer3_weight tensor([[ 1.7534, -0.6233, -0.5366, 0.7915]])
layer3_weight.shape torch.Size([1, 4])
layer3_bias tensor([-0.3791])
layer3_bias.shape torch.Size([1])