清华大学邓俊辉-数据结构MOOC笔记-树的概念及逻辑表示
清华大学邓俊辉-数据结构MOOC笔记-树的概念及逻辑表示
有关概念:
- 与图论略有不同,数据结构中的树:1.需要为每一颗树指定一个特殊的顶点,作为“根”(root),对应rooted-tree;
vertex与node,关系紧密但略有不同,每一个vertex都将以node的形式在计算机中被表示和实现。
child孩子, sibling兄弟(需要定义长幼次序), parent父亲
degree(出)度,即任意节点的孩子的数目。
任何一颗数中顶点数目n和边e的数目同阶,并可以递归证明: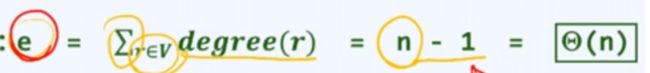
故以后可以使用n为参照,来度量相关算法的复杂度。
兄弟之间也定义了明确次序的数称之为有序树ordered tree。
树结构的拓扑特性
连通性+无环性
路径(或通路)path:V中的k+1个节点,通过E中的k条边依次相连,即称构成一条路径。
路径记为 π = ( v 0 , v 1 ) , ( v 1 , v 2 ) , . . . , ( v k − 1 , v k ) \pi={ (v_{0}, v_{1}), (v_{1}, v_{2}), ... , (v_{k-1}, v_{k}) } π=(v0,v1),(v1,v2),...,(vk−1,vk)
路径长度: ∣ π ∣ = 边 数 = k |\pi|=边数=k ∣π∣=边数=k
(k表边数而不是顶点数)
环路cycle/loop:其中某个顶点(大多是尾顶点),彼此短路,满足 v k = v 0 v_{k}=v_{0} vk=v0。
连通图connected------------无环图acyclic
树:无环联通图、极小连通图、极大无环图
一旦指定了根节点,任一节点v与根之间只存在唯一路径:
path(v, r)=path(v)
可以将所有节点按通路path(v)的长度划分为等价类,并定义depth(v)=|path(v)|,该通路(这里是前面提到的概念)上的节点称为v的祖先ancestor,v是他们的后代descendent(包括v);除去自身应该用“真”(proper)限定。
前驱(祖先)唯一性满足,而后继(后代)的唯一性不一定满足——故称半线性结构。
(每条路径,同深度仅有一个祖先)
不至于引起歧义时:
path from root to v
subtree rooted at v
v
三者的记号path(v)、v、subtree(v)可以混用
所有叶子深度中的最大者,称作(子)树(根)的高度
height(v)=height(subtree(v))
*注意下图中子树高度和全树高度的区别,应有:
子 树 深 度 + 子 树 高 度 ≤ 全 树 高 度 子树深度+子树高度 \le全树高度 子树深度+子树高度≤全树高度
*取等当且仅当该子树有延伸到d-1层的后代(d为全树高度)
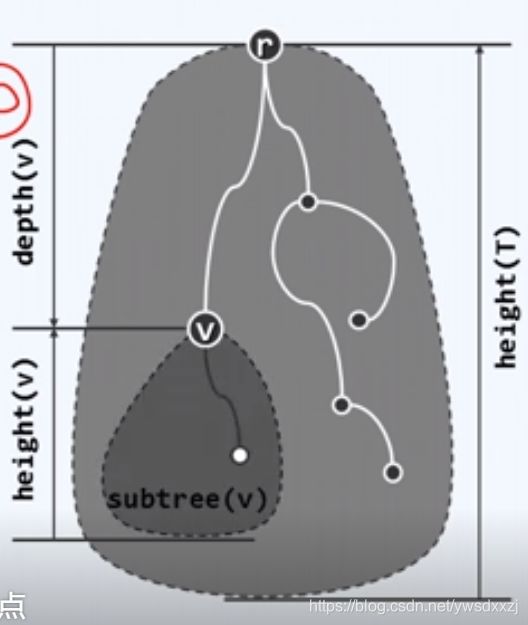
- 根节点是共同祖先,深度为0。
- 单节点的(子)树,高度为0——叶节点高度全为0,但是叶节点的深度中的最大值定义为全树的高度。
- 空子树高度-1。
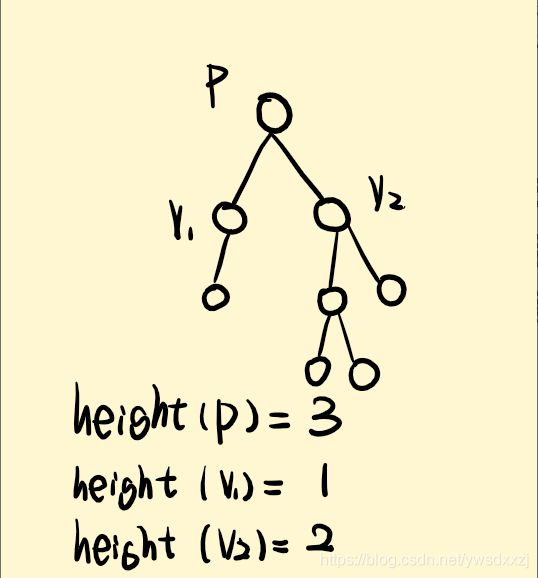
习题:任一颗树中,顶点p是顶点v的父亲,则它们的高度关系是?
提示:不要把高度和深度的概念混淆
基于数组的线性表示
(便于向上查找父亲)
观察易得规律:除根结点外,任一个节点有且仅有一个父节点。
rank:秩,概念同vector
data:数据域
parent:父节点的秩
根节点的parent域定义为-1。
空间性能
每个节点之占用常数空间,故为O(n)
时间性能
- 访问父节点parent():O(1)
- 访问根节点root():O(n),若根节点固定安置于Rank=0处则只需O(1)
- *访问长子firstchild():最坏花费需要**O(n)**遍历整个列表(来查询哪一个元素的parent域等于传入节点的秩)
- *访问兄弟nextSibling():同理O(n)
矛盾:如何自上而下,高效地访问某节点的后代/孩子?
分块(链式)存储
(便于向下查找孩子)
rank:秩,概念同vector
data:数据域
children:链表或数组,表示该节点的所有孩子(对应元素在表中的秩)
最好:长子O(1)
最坏:老幺O(degree(v))
矛盾:自下而上,若要访问某一节点的父亲,则需要遍历序列以一比对(是否在children中存有传入节点的秩),这不合逻辑。且在最坏情况下需要花费**O(n)**才能在表最后一个节点的最后一个孩子处才能命中自己。
以上两种的结合
兼具parent域和children域,方便双向查找
父亲O(1),长子O(1),老幺O(degree(v))
美中不足: ∑ d e g r e e ( v i ) = e = n − 1 ∑degree(v_{i})=e=n-1 ∑degree(vi)=e=n−1
可得平均而言,每一个节点vi的children规模不过O(1);而此处每个节点却需要花费至多O(n)储存,可见这种表示法缺乏常规性。
根源:每一个节点的出度相差悬殊,尤其是叶节点degree(vf)=0
更加深刻的理解
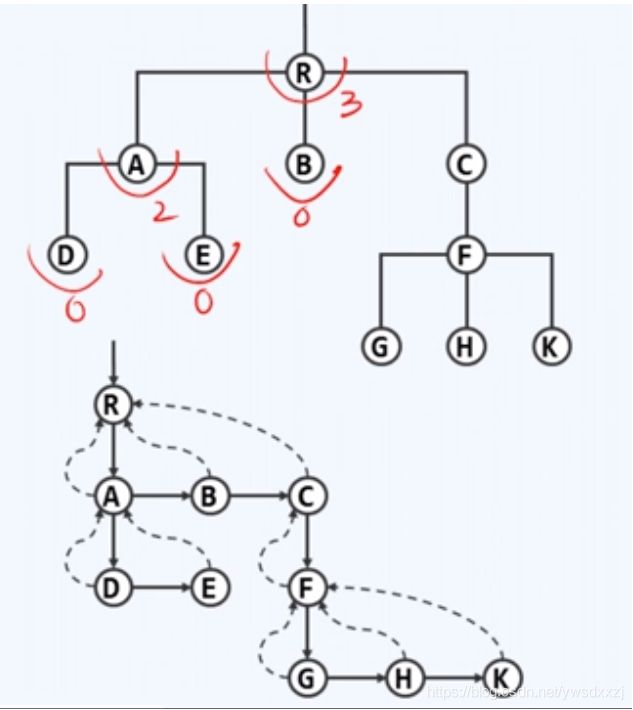
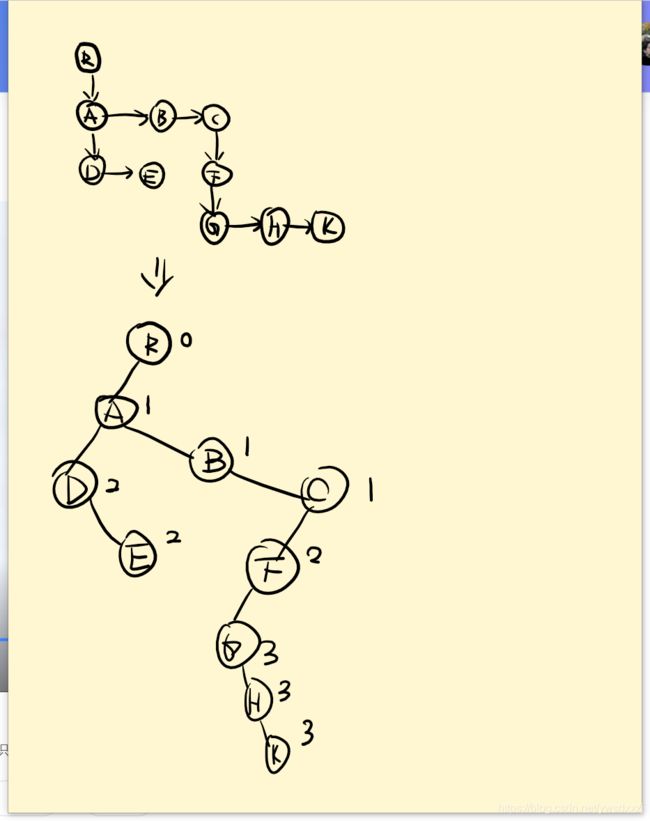
长子+兄弟法:
每一个节点只需记录两个数据(指针),即纵向的firstChild()和横向的nextSibling(),分别指向该节点的长子和下一兄弟。
采用这种表示法,每一个节点都只需记录两个数据,十分规整。
二叉树
-
深度为k的节点,至多2^k个。(当第k层为满时4取等)。
-
h-1<=n<=2^(h+1)-1,下界代表单链条(全序集),上界代表全h+1层全部排满——即称满树。
-
可得高度为h的满树,有h+1层节点;最少第0层,最大第h层,至多2^(h+1)-1个节点;最长通路长度为h+1-1=h。
真二叉树OR满二叉树,即:所有节点的出度均为偶数,非0即2,不存在出度为1的节点。
联系如上的长子兄弟表示法,将firstChild()指针类比于LeftChild(),nextSibling()类比于RightChild(),即可实现任意一颗多叉树到而相应二叉树的转换。