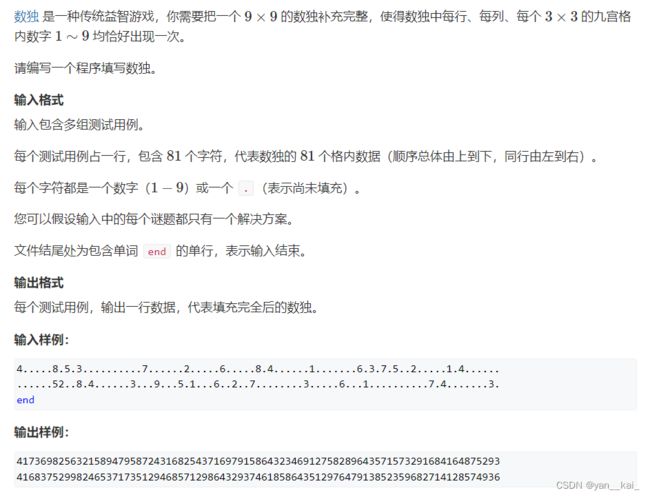
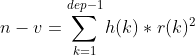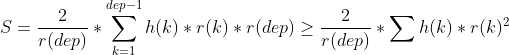搜索（4）dfs的剪枝与优化

一、剪枝方法概述

1.优化搜索顺序

1如在小猫爬山中，按照猫的重量递减的顺序来搜索

2在数独问题中，优先搜索能填的合法数字最少的位置。

2.排除等效冗余

在搜索过程中，如果我们能够判定从搜索树的当前节点上沿着某几条不同的分支的子树是等价的，那么我们只需要对一条子树进行搜索。

3.可行性剪枝

在搜索过程中及时对当前状态进行检查，如果发现分支已经到达递归边界，就执行回溯。

4.最优化剪枝

记录当前已经搜到的最优值，如果目前花费的代价超过了最优值，则直接剪枝

5.记忆化搜索

二、例题

1.小猫爬山

直觉：遍历所有猫，深搜过程记录当前已经开的车数量，记录已经搜过了几只猫。

深搜过程中，由于猫的重量不可能每次掐好填满某辆缆车，因此先遍历之前的缆车看能不能放下，若可以就放，不行就新开一辆。每次dfs下一层之后都需要回溯，因为不确定放到哪个缆车才是最优方案

剪枝：如果已经开的车的数量大于要求，就剪枝（可行性）

       如果当前开的车的数量大于目前最优解，剪枝（最优化）

#include
#include
#include
using namespace std;

const int N =20;

int n;
int w;
int c[N];
int cab[N];//记录某条缆车装了多少重量
int ans=N;

//对于每一只猫有两种决策 放入已租用的缆车 和 直接新开一个缆车
void dfs(int now,int cnt)//已经搜索了几只猫   当前用了多少个缆车
{
    if(cnt>=ans) return ;
    if(now==n)
    {
        ans=cnt;
        return;
    }

    for(int i=1;i<=cnt;i++)//分配到已租用的缆车
    {
        if(cab[i]+c[now]<=w)
        {
            cab[i]+=c[now];
            dfs(now+1,cnt);
            cab[i]-=c[now];
        }
    }
    //新开
    cab[cnt+1]+=c[now];
    dfs(now+1,cnt+1);
    cab[cnt+1]-=c[now];

}


int main()
{
    cin>>n>>w;
    for(int i=0;i>c[i];
    sort(c,c+n,greater());
    dfs(0,0);
    cout<

二、数独问题

 先看看简单版数独

#include
#include
#include
using namespace std;
const int N =11;
bool row[N][N],col[N][N],cell[N][N][N];
char g[N][N];


bool dfs(int x,int y)
{
    if(y==9)  x++,y=0;
    if(x==9)
    {
        for(int i=0;i<9;i++)
            cout<>g[i];
        for(int j=0;j<9;j++)
        {
            if(g[i][j]!='.') 
            {
                int t=g[i][j]-'1';
                row[i][t]=col[j][t]=cell[i/3][j/3][t]=true;
            }
        }
        
    }
    
    
    dfs(0,0);
    return 0;
}

现在考虑剪枝：

优化搜索顺序：当有几个空位的数字确定时，由于数独的特性，会导致其他很多空位的选择变少，因此我们要从可选择数字最少的地方开始深搜。

排除等效冗余:任意一个状态下,我们只需要找一个位置填数即可,而不是找所有的位置和可填的数字.
位运算:很明显这里面check判定很多,我们必须优化这个check,所以我们可以对于,每一行,每一列,每一个九宫格,都利用一个九位二进制数保存,当前还有哪些数字可以填写.

#include
#include
#include
using namespace std;

const int N =9,M=1<>j&1;
    
    while(cin>>str,str[0]!='e')
    {
        init();//初始化为每个位置每个数都可以填
        
        int cnt=0;
        for(int i=0,k=0;i

三、木棒

 直觉想法：设定原始木棒长度len，当前正在拼的木棒长度cab，当前正在拼第stick个原始木棒，接下来该从哪个木棒开始选，上次选了第i根，则last=i+1，拼新一根时last=0）。当cab==len时，拼下一根。从last开始枚举，试探将别的木棒拼入，能拼入的要求是：没被选择过、cab+这根木棒的长度小于len。拼入之后就继续dfs，没有木棒可以拼入就return false

剪枝：

1.最优性剪枝：从小到大枚举长度，如果成功就直接break了。

2.可行性剪枝：可以预先知道在len长度下将有多少根木棒，如果当前已经拼好的木棒超过这个数，直接返回false：当该木棍在开头和结尾都不可以使用的时候,那么该方案就失败了

3.排除等效冗余：如果长度为l的木棒已经被尝试过，回溯之后继续枚举时，也不需要在枚举长度为l的其他木棒，因为子树都是等价的。

补充：

如果木棍在第一个位置不合法的话：假设我们把该木棍用在其他的位置合法了，那么我们就可以把顺序颠倒一下，把该木棒放到第一个也是合法的，该假设与条件不符。
同理：如果木棍在最后一个位置不合法的话：假设我们把该木棍用在其他的位置合法了，那么我们就可以把顺序颠倒一下，把该木棒放到最后一个也是合法的，该假设与条件不符。

但是，放到中间的木棍就不一样了，因为这种情况也可能是该木棍和前面组成该木棒的某一个木棍不合适，所以才造就了他的不合法。在这种情况下，可能换一种方法就合适了

#include
#include
#include
using namespace std;

const int N =70;

int a[N];
int n;
int len;
int cnt;
bool st[N];


//正在拼第stick根原始木棒
//cab当前在拼的原始木棒的长度
//接下来该从那个木棒开始选择（上一次选了i,last=i+1,拼新一根时last=0）
bool dfs(int stick,int cab,int last)
{
    if(stick>cnt) return true;
    if(cab==len) return dfs(stick+1,0,0); //拼新一根 last置为0;
    
    int fail=0;//剪枝2
    for(int i=last;i>n,n!=0)
    {
        int val=0,sum=0;
        for(int i=0;i>a[i];
            sum+=a[i];val=max(val,a[i]);
        }
        sort(a,a+n);
        reverse(a,a+n);
        
        for(len=val;len<=sum;len++)
        {
            if(sum%len) continue;
            
            cnt=sum/len; //该有多少根原始木棒
            memset(st,false,sizeof st);
            if(dfs(1,0,0)) break;
        }
        cout<

四、生日蛋糕

  外表面：侧面积加上表面

搜索框架：从下往上搜索，枚举每层蛋糕的半径和高度，本题蛋糕层数的计数从上往下

搜索面对的状态：正在枚举第dep层，当前外表面积s，当前体积v和第dep+1层的高度和半径。因此我们可以用 h 和r 两个数组记录每层的高度和半径

在搜索过程中，上表面的面积之和等于最低层的圆面积，因此可以在第M层直接累加到s中，这样在第M-1层之前的搜索中，只需要计算侧面积

剪枝：

1.上下界剪枝：取极限情况，在枚举第dep层时，r一定要大于等于dep，因为r递增且为正整数。考虑极限情况，r一定要小于dep+1层的半径-1，取极限情况：当前是最后一层且H最小=1，则r最大值一定小于sqrt（N-v）。因为.

        其次，h的取值要在dep到dep+1层的H再-1。同样的还要小于（N-v）/R^2.

2.优化搜索顺序：R为平方项，对体积影响大，所以先枚举R，在枚举H

3.可行性剪枝：

可以预处理从上往下前i层的最小侧面积和体积。

如果当前体积v加上1~dep-1的最小体积大于N，则剪枝

4.最优化剪枝：如果当前表面积s大于当前最优值，则剪枝

5.最优化剪枝：利用h和r数组， 1~dep-1层的体积可以表示出来，表面积也可以表示出来。

所以当大于已经搜到的答案时，剪枝

#include
#include
#include
#include
using namespace std;

const int N=25,INF=1e9;

int n,m;
int minv[N],mins[N];
int H[N],R[N];
int ans=INF;

void dfs(int u,int v,int s)
{
    if(v+minv[u]>n) return ;
    if(s+mins[u]>=ans) return ;
    if(s+2*(n-v)/R[u+1]>ans) return ;

    if(u==0)
    {
        if(v==n) ans=s;
        return;
    }
    for(int r=min(R[u+1]-1,(int)sqrt(n-v));r>=u;r--)
        for(int h=min(H[u+1]-1,n-v/r/r);h>=u;h--)
        {
            int t=0;
            if(u==m) t=r*r;
            R[u]=r,H[u]=h;
            dfs(u-1,v+r*r*h,s+2*r*h+t);
        }
}



int main()
{
    cin>>n>>m;

    for(int i=1;i<=m;i++)
    {
        minv[i]=minv[i-1]+i*i*i;
        mins[i]=mins[i-1]+2*i*i;
    }

    if(minv[m]>n)//无解
    {
        puts("0");
        return 0;
    }

    R[m+1]=H[m+1]=1e9;//  因为R,H的搜索范围  且dfs用到R[m+1]

    dfs(m,0,0);
    cout<

总结

来自《算法竞赛进阶指南》：
搜索算法面对的状态可以看做一个多元组，其中每一元都是问题中的一个维度。一定要注意提取这些信息，构建合适的搜索框架

剪枝过程实际就是针对每个维度与该维度的边界条件，加以推导，得到一个相应的不等式来减少搜索树分支的扩张。

为了进一步提高搜索的效率，除了当前花费的代价外，还可以计算未来至少需要花费的代价进行预算。