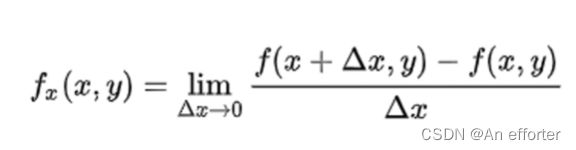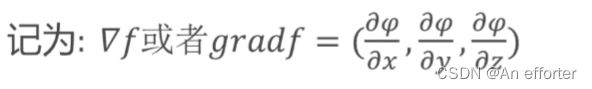Pytorch框架的学习(4)
目录
1.Pytorch与autograd(自动计算梯度)-导数-方向导数-偏导数-梯度的概念
2.梯度与机器学习中的最优解
3.Variable is Tensor(案例中见)
4.如何计算梯度
5.关于Autograd的几个概念
1.Pytorch与autograd(自动计算梯度)-导数-方向导数-偏导数-梯度的概念
(1).什么是导数?
导数(一元函数)是变化率、是切线的斜率、是瞬时速度。
(2).什么是方向导数?
函数在A点无数个切线的斜率的定义。每一个切线都代表一个变化的方向。
在上面图片中左边的a点画出了多个切线,方向都是不同。再看右边的A点,画出了这一点的切线,这就是某一方向的导数(方向导数)。
(3).什么是偏导数?
多元函数降维时候的变化,比如:二元函数固定y,只让x单独变化,从而看成是关于x的一元函数的变化来研究。
(4).什么是梯度?
函数在A点无数个变化方向中变化最快的那个方向。从而寻找到最优解。
2.梯度与机器学习中的最优解
上面说了,就是在无数个变化方向中找到变化最快的那个方向,经过多次迭代,找到最优解。
再做模型的时候,是有理论基础与优化函数的,在机器学习中有三大学习:有监督学习,无监督学习,半监督的学习。
有监督学习:简单的说有样本、有标签,进行训练。就比如说,判断男女,我们就拿出一些外貌特征作为样本,打上男女标签。最后训练出模型,就可以输入属性,得到结果。常见的有LDA、SVM、深度学习。
无监督学习:有样本,无标签的,常见的有聚类、PCA
半监督学习: 有三个条件:1.弱标签(标注的不准确),2.伪标签(通过某种方法进行标注的,比如说聚类),3.一半有标签一半无标签。
学过机器学习的同学一定都知道 Y=f(X)。 f()就是网络结构,就像函数一元,二元,多元函数。输入一个X,得到一个Y,网络结构肯定有很多参数W,b等等,可写为这样的f(w,b,x),为了得到最优解不断迭代,优化参数,减小loss=||f(w,b,x)- Y真 ||^2,才能得到最优解。
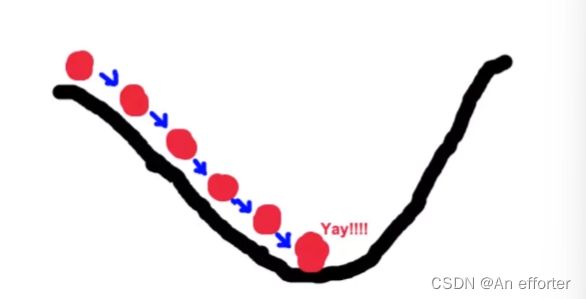
再深入一点,我们可以把f(w,b,x),这个函数想象成一个二元一次方程,开口向上的凹形曲线,一定是有最小值的,最小值就是最优解,这一点是loss最小值的地方,我们怎么样去找到那?
只要沿着梯度下降最快的方向,不断地调整,一个点不是,再往下找,当调整到最低谷的时候,就找到了这个点,参数w,b就找到了。我们还是最快的速度找的,因为我们找的是梯度下降最快的方向。方法就是求导。
还有一点就是我们的函数(网络模型)比较复杂,在编写代码时候,就用到了梯度下降法。
还有调整问题,我们每次迭代,需要调多少那,那就与学习率有关系了。(后面更新相关的概念)。
3.Variable is Tensor(案例中见)
- 目前Variable已经与Tensor合并。
- 每个tensor通过requires_grad来设置是否计算梯度。用来冻结某些层的参数
4.如何计算梯度
- 链式法则:两个函数组合起来的复合函数,导数等于里面函数代入外函数值的导乘以里面函数之导数。(大学里学过)
举个例子: y=2x,Z=y*y,求dz/dx。
5.关于Autograd的几个概念
grad vs grad_fn
- grad:该Tensor的梯度值,每次在计算backward时都需要将前一时刻的梯度归零,否则梯度值会一直累加。
- grad_fn:叶子节点通常为None,只有结果节点的grad_fn才有效,用于指示梯度函数是哪种类型。
backward函数
- torch.autograd.backward(tensors,grad_tensors=None,retain_graph=None,create_graph=False)
tensor:用于计算梯度的tensor,torch.autograd.backward(z)==z.backward()
grad_tensors:在计算矩阵的梯度时会用到。他其实也是一个tensor, shape
一般需要和前面的tensor保持一致。
retain_graph:通常在调用一次backward后,pytorch会自动把计算图销毁,所以要想对某个变量重复调用backward,则需要将该参数设置为True
create_graph: 如果为True,那么就创建一个专门的graph of thederivative,这可以方便计算高阶微分。
torch.autograd.grad()函数
- def grad(outputs, inputs, grad_outputs=None, retain_graph=None,create_graph=False, only_inputs=True, allow_unused=False)
计算和返回output关于 inputs的梯度的和。
outputs :函数的因变量,即需要求导的那个函数
inputs:函数的自变量,定义多个tensor。
grad_outputs : 同backward
only_inputs:只计算input的梯度
allow_unused( bool,可选)∶如果为False,当计算输出出错时(因此他们的梯度永远是0)指明不使用的inputs。
torch.autograd包中的其他函数
- torch.autograd.enable_grad:启动梯度计算的上下文管理器
- torch.autograd.no_grad :禁止梯度计算的上下文管理器
- torch.autograd.set grad_enabled(mode):设置是否进行梯度计算的上下文管理器。
torch.autograd.Function
每一个原始的自动求导运算实际上是两个在Tensor上运行的函数
- forward函数计算从输入Tensors获得的输出Tensors
- backward函数接收输出Tensors对于某个标量值的梯度,并且计算输入Tensors相对于该相同标量值的梯度
- 最后,利用apply方法执行相应的运算
比照着下面的代码看:
在底层,每一个原始的自动求导运算实际上是两个在Tensor上运行的函数。其中,forward函数计算从输入Tensors获得的输出Tensors。而backward函数接收输出Tensors对于某个标量值的梯度,并且计算输入Tensors相对于该相同标量值的梯度。
在PyTorch中,我们可以很容易地通过定义torch.autograd.Function的子类并实现forward和backward函数,来定义自己的自动求导运算。之后我们就可以使用这个新的自动梯度运算符了。然后,我们可以通过构造一个实例并像调用函数一样,传入包含输入数据的tensor调用它,这样来使用新的自动求导运算。
import torch
'''
1.ctx是context的缩写, 翻译成"上下文; 环境"
2.ctx专门用在静态方法中
3.self指的是实例对象;
而ctx用在静态方法中, 调用的时候不需要实例化对象, 直接通过类名就可以调用,
所以self在静态方法中没有意义.
4.自定义的forward()方法和backward()方法的第一个参数必须是ctx;
ctx可以保存forward()中的变量,以便在backward()中继续使用.
'''
class line(torch.autograd.Function):
def forward(ctx,w,x,b):
'''
前向传播
:param ctx: 上下文管理器
:param w:
:param x:
:param b:
:return:
ctx.save_for_backward(a, b)能够保存forward()静态方法中的张量,
从而可以在backward()静态方法中调用.
'''
ctx.save_for_backward(w,x,b)
return w*x+b
def backward(ctx,grad_out) :
w, x, b = ctx.saved_tensors
'''
通过w,x,b= ctx.saved_tensors重新得到w,x,b.
'''
# 获取在前向传播里面的变量信息
w, x, b = ctx.saved_tensors
# 对w求导
# 上一级梯度乘以当前梯度
grad_w = grad_out * x
# 对x求导
grad_x = grad_out * w
# 对b求导
grad_b = grad_out
return grad_w, grad_x, grad_b
w = torch. rand(2,2,requires_grad=True)
x = torch. rand(2,2, requires_grad=True)
b = torch. rand(2,2, requires_grad=True)
# 使用apply调用相应的运算
out=line.apply(w,x,b)
out.backward ( torch.ones(2,2))
print(w, x, b )
# 查看梯度值
print(w.grad, x.grad, b.grad)对于w*x+b,对于w的求导后,是x。对x求导后,是w。对b求导后是1。结果如上。