机器学习实验 - 决策树

报告内容仅供学习参考，请独立完成作业和实验喔~

一、报告摘要

1.1 实验要求

（1）了解pandas和sklearn数据科学库功能；
（2）学习在conda或pip环境下安装库；
（3）掌握决策树原理，包括划分选择中三种经典指标信息增益、增益率和基尼指数的优缺点，剪枝处理方法及作用、连续值与缺失值处理等；
（4）基于多分类数据集，使用pandas和sklearn库处理数据以及选择决策树模型，通过精确率、召回率和F1值度量模型性能，对比不同剪枝策略、不同划分选择标准的性能表现，给出模型的特征重要度。

1.2 实验思路

\qquad 使用Python读取数据集信息并利用sklearn训练决策树模型，随后使用生成的决策树实现多分类预测，调整决策树划分方法及剪枝方法，并根据精确率、召回率和F1值度量模型性能。

1.3 实验结论

\qquad 本实验训练了4个不同超参数的决策树模型，并通过计算精确率、召回率和F1值度量各模型性能。在训练得到的4个决策树模型中，使用Gini、max_depth=4、ccp_alpha=0.01参数的模型性能最优，其F1值为0.98005。

二、实验内容

2.1 方法介绍

\qquad 决策树(decision tree)是一种基本的分类与回归方法。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程，由节点和有向边组成，结点有2种结构：内部节点表示一个特征或属性，叶节点表示一个类别。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。
\qquad 学习时，利用训练数据根据损失函数最小化的原则建立决策树模型。预测时，对新的数据，利用决策树模型进行分类。决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪。
（1）特征选择
\qquad 特征选择是选择对训练数据分类能力强的特征，提高决策树的学习效率。直观上来讲，如果一个特征比另外一个特征有更好的分类能力，那就应该选择它，我们按照这个特征将训练数据分割成子集，各个子集在当前条件下就会有最好的分类结果。
\qquad 常用的准则：信息增益、信息增益比、基尼指数等。
\qquad 信息增益：以某特征划分数据集前后的熵的差值。当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分之后的熵更低，由于划分前的熵是一定的，因此信息增益更大，因此信息增益有偏向取值较多的特征这一缺点。
\qquad 信息增益比本质是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。当特征取值较少时H_A(D)的值较小，因此其倒数较大，因而信息增益比较大。故信息增益比有偏向取值较少的特征的缺点。
\qquad 基尼指数表示在样本集合中一个随机选中的样本被分错的概率。基尼指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。
（2）决策树的生成
\qquad 决策树生成算法：ID3（信息增益）、C4.5（信息增益比）、CART树（基尼指数）等。
\qquad 1）ID3算法
\qquad ID3算法是决策树的一个经典的构造算法，内部使用：信息熵，信息增益，来进行构建：每次迭代选择信息最大的特征属性作为分割属性。在ID3算法中节点纯度的度量为“信息熵”，分裂特征的选择用的是信息增益度作为衡量指标。
\qquad ID3算法只支持离散（类别型）特征属性，不支持连续特征属性。故ID3算法使用连续属性时要将连续属性进行离散化；此外ID3构建的是多叉树。
\qquad 优点：决策树构建速度快；实现简单。
\qquad 缺点：计算依赖于特征取值数目较多的特征，而属性值最多的属性并不一定最优；ID3算法不是递增算法；ID3算法是单变量决策树，对于特征属性之间的关系不会考虑；抗噪性差；只支持小数据等。
\qquad 2）C4.5算法
\qquad C4.5实际上是对ID3算法进行的优化算法。也是一种经典的决策树构建算法。使用信息增益率来取代ID3算法中的信息增益，并在树的构造过程中进行剪枝优化。同时，能够自动完成对连续属性的离散化处理，构建的是多分支的决策树。在分割属性时，C4.5算法选择的是信息增益率最大的属性。
\qquad 优点：产生的规则易于理解；准确率较高；实现简单。
\qquad 缺点：对数据集需要进行多次顺序扫描和排序，所以效率较低；只适合小规模数据集等。
\qquad 3）CART算法
\qquad CART既可以做分类任务，也可以做回归任务。在做分类树时，使用基尼系数作为数据纯度的度量指标，在做回归树时使用均方差作为数据纯度的度量指标。使用基尼增益率作为分割属性选择的标准，允许特征重复使用，构造的为二叉树。
\qquad 此外，在目前的使用中，CART算法是三种算法中最常用的一种决策树构建算法

（3）决策树的修剪
\qquad 决策树修剪主要降低模型复杂度，防止模型过拟合。主要分为：预剪枝和后剪枝。预剪枝：决策树生成过程中，提前停止某些分支生长。后剪枝：计算节点信息量（经验熵），自下而上地回缩节点。

2.2 实验细节

2.2.1 实验环境

硬件环境：Intel® Core™ i5-10300H CPU + 16G RAM
软件环境：Windows 11 家庭中文版 + Python 3.8

2.2.2 实验过程

（1）数据集引入及分割
\qquad 将数据集按2/3训练集，1/3测试集的比例进行随机分割。

X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=1/3,random_state=0)
print('数据集样本数：{},训练样本数：{},测试集样本数：{}'.format(len(X),len(X_train),len(X_test)))

（2）训练决策树
\qquad 利用sklearn提供的DecisionTreeClassifier()方法构造决策树，DecisionTreeClassifier()方法的常用参数如下：
\qquad 划分准则criterion，可选：基尼指数gini、信息增益entropy、对数损失log_loss，默认gini；
\qquad 最大树深度max_depth，整数型，默认为不限制；
\qquad 最大叶节点数max_leaf_nodes，整数型，默认为不限制；
\qquad 最大代价复杂度ccp_alphat，非负浮点型，默认为0.0。
\qquad 我们这里分别利用三种不同的划分准则，以4为最大深度对树进行前剪枝。以使用基尼指数的决策树为例，训练并查看树结构，代码如下：

gini_model = DecisionTreeClassifier(criterion='gini',max_depth=4,splitter='best')
gini_model.fit(X_train,y_train)
gini_y_pred = gini_model.predict(X_test)
tree.plot_tree(gini_model)
plt.show()

\qquad 得到的树结构如下图：

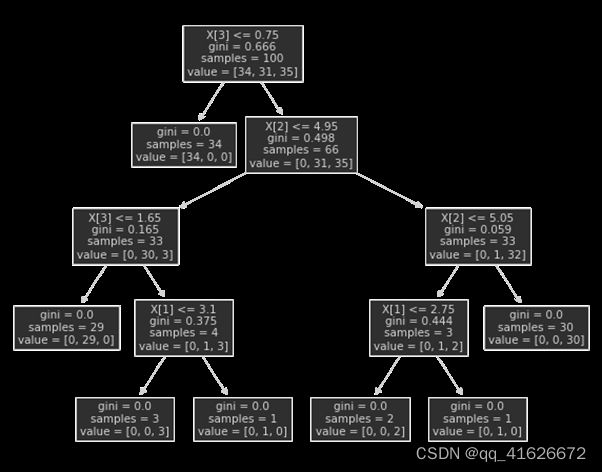
\qquad 可以看到，排除根节点，这颗决策树为4层的二叉树，这也符合基尼指数划分方法的特点。计算该树的精确率、召回率和F1度量值，得到如下结果：

\qquad 继续训练其他两种划分方式，在同等预剪枝条件下，对于信息增益Entropy方式划分，得到如下决策树及性能结果：

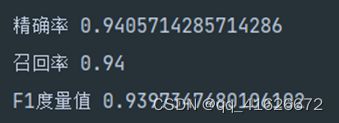
\qquad 对于对数损失log_loss方式划分，得到如下决策树及性能结果：

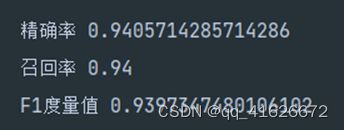
\qquad 根据对比，我们可以发现，在同等预剪枝条件下，以基尼系数划分的决策树性能更优。
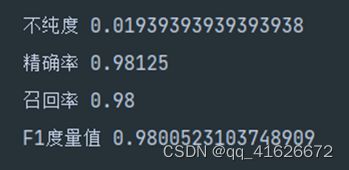
（3）利用CCP进行后剪枝
\qquad CCP（Cost Complexity Pruning）为代价复杂度剪枝法，核心思想为在树构建完成后，对树进行剪枝简化，使以下损失函数最小化：
$$L=\sum _{i=1}^T\frac{N_i}{N}{L}_i+\alpha T$$
\qquad 其中，T为叶子节点个数，N为所有样本个数，N_i为第i个叶子节点上的样本数，L_i为第i个叶子节点的损失函数，α为待定系数，用于确定惩罚节点个数，引导模型用更少的节点。
\qquad 具体操作中，首先使用cost_complexity_pruning_path()方法需要计算树的CCP路径，得到alpha与树纯度的关系，具体代码及结果如下：

pruning_path = gini_model.cost_complexity_pruning_path(X_train, y_train)
print("ccp_alphas:",pruning_path['ccp_alphas'])
print("impurities:",pruning_path['impurities'])

\qquad 其意义为，当0 \qquad 这里设置可以接受的不纯度为0.03874878，故在0.00969697和0.03519062之间选择ccp_alpha的值，令ccp_alpha=0.01,再次进行训练，得到如下结果：

2.3 实验数据介绍

\qquad 实验数据为来自UCI的鸢尾花三分类数据集Iris Plants Database。
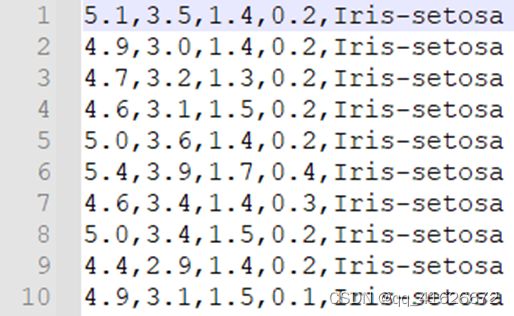
数据集共包含150组数据，分为3类，每类50组数据。每组数据包括4个参数和1个分类标签，4个参数分别为：萼片长度sepal length、萼片宽度sepal width、花瓣长度petal length、花瓣宽度petal width，单位均为厘米。分类标签共有三种，分别为Iris Setosa、Iris Versicolour和Iris Virginica。
\qquad 数据集格式如下图所示：

\qquad 为方便使用，也可以直接调用sklearn.datasets库中提供的load_iris()方法加载处理过的鸢尾花分类数据集。

2.4 评价指标介绍

\qquad 评价指标选择精确率P、召回率R、F1度量值F1，计算公式如下：
$$P=\frac{TP}{TP+FP}$$
$$R=\frac{TP}{TP+FN}$$
$$F1=\frac{2\ast P\ast R}{P+R}$$
\qquad 具体代码实现时，可以直接调用sklearn库中的相应方法进行计算。

2.5 实验结果分析

\qquad 根据计算，对于二分类数据集，可以得到如下结果：

超参数	Gini、max_depth=4	Entropy、max_depth=4	Log_loss、max_depth=4	Gini、max_dpeth =4、ccp_alpha=0.01
精确率P	0.96	0.94057	0.94057	0.98125
召回率R	0.96	0.94	0.94	0.98
F-Score(β=1)	10.96	0.93973	0.93973	0.98005

三、总结及问题说明

\qquad 本次实验的主要内容为使用决策树分类鸢尾花三分类数据集，并调整参数，计算生成模型的精确度Precision、召回率Recall和F1度量值，从而对得到的模型进行评测，弄清参数与效果之间的关系，选出更优的决策树模型。
\qquad 在本次实验中，未遇到很难解决的问题，可以选出效果较好的决策树模型，完成分类任务。

四、参考文献

[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] 决策树–信息增益，信息增益比，Geni指数的理解[EB/OL]. [2022-5-22]. https://blog.csdn.net/Tomcater321/article/details/80699044.
[3] 决策树构建算法—ID3、C4.5、CART树[EB/OL]. [2022-5-22]. https://blog.csdn.net/sinat_42247418/article/details/122221809.
[4] 细讲sklearn决策树后剪枝(带例子) [EB/OL]. [2022-5-22]. https://blog.csdn.net/ywj_1991/article/details/123021016.
[5] sklearn.tree. DecisionTreeClassifier — scikit-learn 1.1.1 documentation[EB/OL]. [2022-5-22]. https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html.

附录：实验代码

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
from matplotlib import pyplot as plt
from sklearn import tree
iris = load_iris()

plt.rcParams['figure.figsize'] = (10, 8)
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=1/3,random_state=0)
print('数据集样本数：{},训练样本数：{},测试集样本数：{}'.format(len(X),len(X_train),len(X_test)))

gini_model = DecisionTreeClassifier(criterion='gini',max_depth=4,splitter='best')
gini_model.fit(X_train,y_train)
gini_y_pred = gini_model.predict(X_test)
tree.plot_tree(gini_model)
plt.show()
print("精确率",precision_score(y_test, gini_y_pred, average='weighted'))
print("召回率",recall_score(y_test, gini_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, gini_y_pred, average='weighted'))

gain_model = DecisionTreeClassifier(criterion='entropy',max_depth=4,splitter='best')
gain_model.fit(X_train,y_train)
gain_y_pred = gain_model.predict(X_test)
tree.plot_tree(gain_model)
plt.show()
print("精确率",precision_score(y_test, gain_y_pred, average='weighted'))
print("召回率",recall_score(y_test, gain_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, gain_y_pred, average='weighted'))

loss_model = DecisionTreeClassifier(criterion='log_loss',max_depth=4,splitter='best')
loss_model.fit(X_train,y_train)
loss_y_pred = loss_model.predict(X_test)
tree.plot_tree(loss_model)
plt.show()
print("精确率",precision_score(y_test, loss_y_pred, average='weighted'))
print("召回率",recall_score(y_test, loss_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, loss_y_pred, average='weighted'))

gini_model = DecisionTreeClassifier(criterion='gini',max_depth=4,splitter='best')
gini_model.fit(X_train,y_train)
gini_y_pred = gini_model.predict(X_test)
acc = accuracy_score(y_test,gini_y_pred)
print('准确率：',acc)

#计算ccp路径
pruning_path = gini_model.cost_complexity_pruning_path(X_train, y_train)
print("ccp_alphas:",pruning_path['ccp_alphas'])
print("impurities:",pruning_path['impurities'])

#CCP后剪枝
clf = tree.DecisionTreeClassifier(max_depth=4,random_state=0,ccp_alpha=0.01)
clf = clf.fit(X_train, y_train)
#计算纯度
is_leaf =clf.tree_.children_left ==-1
tree_impurities = (clf.tree_.impurity[is_leaf]* clf.tree_.n_node_samples[is_leaf]/len(y_train)).sum()
clf_y_pred = clf.predict(X_test)
tree.plot_tree(clf)
plt.show()

print("不纯度",tree_impurities)
print("精确率",precision_score(y_test, clf_y_pred, average='weighted'))
print("召回率",recall_score(y_test, clf_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, clf_y_pred, average='weighted'))