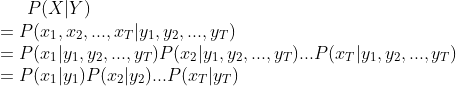隐马尔可夫模型（HMM）——从理论证明、算法实现到实际应用

目录

历史简述

建模

HMM一般表述

观测序列生成机理

经典问题一之前向算法

经典问题二

经典问题三之viterbi算法

viterbi算法求解案例

viterbi算法代码实现

HMM模型应用

---

历史简述

        对于马尔可夫链，比较多的说法是：由俄国数学家安德雷·马尔可夫（Андрей Андреевич Марков）在1906-1907年间发表的一篇研究中而来，研究中为了证明随机变量间的独立性不是弱大数定律（weak law of large numbers）和中心极限定理（central limit theorem）成立的必要条件，构造了一个按条件概率相互依赖的随机过程，并证明其在一定条件下收敛于一组向量。在这个研究被提出之后，真的是一发不可收拾，后人在此基础上相继提出了各种模型，比如保罗·埃伦费斯特（Paul Ehrenfest）和Tatiana Afanasyeva在1907年使用马尔可夫链建立了Ehrenfest扩散模型（Ehrenfest model of diffusion） 。1912年亨利·庞加莱（Jules Henri Poincaré）研究了有限群上的马尔可夫链并得到了庞加莱不等式（Poincaré inequality）  。1931年，安德雷·柯尔莫哥洛夫（Андрей Николаевич Колмогоров）在对扩散问题的研究中将马尔可夫链推广至连续指数集得到了连续时间马尔可夫链，并推出了其联合分布函数的计算公式  。独立于柯尔莫哥洛夫，1926年，Sydney Chapman在研究布朗运动时也得到了该计算公式，即后来的Chapman-Kolmogorov等式  。二十世纪50年代，前苏联数学家Eugene Borisovich Dynkin完善了柯尔莫哥洛夫的理论并通过Dynkin公式（Dynkin formula）将平稳马尔可夫过程与鞅过程（martingale process）相联系。

        不幸地是，今天，马尔可夫模型被应用在了机器学习中，困扰着我…… ，对于历史真实性，不做考证，随它遗留在历史角落中……

---

建模

        在机器学习中，马尔可夫链(Markov chain)得到了极大的应用。它究竟是什么？又能解决什么样问题呢？先从一个最简单的生活案例谈起（以下简称“案例“）。

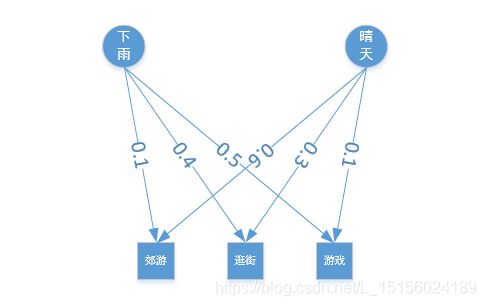
        小宝有3天假期，每天可以从“郊游”、“逛街”和“打游戏”中选择一种活动。如果是晴天，小宝更可能选择去郊游，而如果下雨，小宝就可能会待在家打游戏了。小宝知道如下信息：

（1）当天的天气只与前一天的天气有关；

（2）第一天下雨的概率为0.6，晴天的概率为0.4；

（3）天气变化概率如下：如果前一天下雨，那么第二天仍然下雨的概率为0.7，而转为晴天的概率为0.3；但是如果前一天是晴天，则第二天有0.6的概率是晴天，而有0.4的概率将会下雨；

小宝根据天气情况如下选择活动：

（a）如果下雨，3个活动的被选择的概率分别为：0.1,  0.4,  0.5；

（b）如果是晴天，3个活动的选择概率分别是：0.6,  0.3,  0.1；

现在如果已经知道了小宝3天假期安排的活动按顺序分别是：郊游、逛街、游戏，我们会面临如下三个问题：

（i）小宝这样安排活动的可能性多大？

（ii）上面（1）~（3）假设的这些概率值是不是导致小宝最后选择这3种活动的最佳概率呢？也就是说有没有其他的这些概率值更可能导致小宝选择这3种活动？

（iii）这3天的天气情况分别是？

 

        下面以案例为基础进行建模来解决这三个问题。这个模型就是马尔可夫模型（Hidden Markov Model，HMM）。下面开始建模。

（1）天气——隐状态

        使用表示连续T天的天气情况，每个可以看成一个随机变量，可能的取值为，称为隐状态空间，因为通常天气情况是无法观察的。对于案例来说，天气情况序列为，状态空间为S={ 下雨， 晴天}，如果第一天是晴天，则=晴天。

（2）活动——观测状态

        使用表示连续T天小宝选择的活动，每个也是一个随机变量，可能的取值为，称为观测状态空间。对于案例来说，活动序列为，观测状态空间为O={ 郊游，逛街，游戏 }。

（3）齐次马尔科夫链假设

       天气变化的概率可以使用条件概率表示，它表示在第1天到第t-1天的天气情况之后，第t天出现何种天气的概率。根据案例中的（1），当天的天气只与前一天的天气有关，我们有

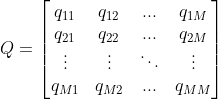
这就是齐次马尔科夫链假设。根据隐状态空间的各种状态的转移的可能，构成如下阶矩阵：

表示由隐状态转移到的概率，称之为隐状态转移矩阵。对案例来说，转移矩阵如下：

   

注意到隐状态转移矩阵和时刻t无关。可以使用如下图来表示：

（4）观测独立性假设

        即任意时刻t的观测状态只仅仅依赖于当前时刻的隐藏状态，这是为了简化模型。如果在时刻t的隐藏状态, 而对应的观察状态为, 则该时刻在隐藏状态下观察值到的的概率记为，如下：

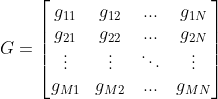
考虑所有可能的情况，构成一个阶矩阵，如下：

表示在状态为的情况下，观测到的概率，称之为观测状态矩阵。对于案例来说，如下：

.

注意到观测状态转移矩阵和t也无关。观测状态矩阵可以使用如下图表示：

（5）初始隐状态分布

        案例中的信息（3）是天气的初始状态，也就是，概率分布如下：

	下雨	晴天
	0.6	0.4

称之为隐状态初始分布。

        有了上面这些之后，马尔科夫模型就可以如下形式地表示：

其中F是隐状态初始分布，Q是隐状态转移矩阵，G是观测状态矩阵。

案例的马尔可夫模型可以直观地用下面这个图来表示：

图中表示三天的隐状态和观察状态之间的关系。箭头表示依赖关系。熟悉概率图的知道，这就是HMM的概率图。现在对案例中三个问题进行建模，分别如下：

（1） 估计观察序列X概率

        即给定模型和观测序列，计算在模型λ下观测序列X出现的概率P(X|λ)。

（2）模型参数的学习问题

        即给定观测序列，在满足马尔科夫条件和独立性假设前提下，求解模型，使该模型下观测到序列X的条件概率P(X|λ)最大，即：。

（3）预测问题，也称为解码问题

        即给定模型和观测序列，求给定观测序列条件下，最可能出现的对应的状态序列。

这三个问题是HMM模型的三个经典问题。好在我们都可以解决。

---

HMM一般表述

        下面我们给出HMM模型的一般表述。首先我们假设是所有可能的隐藏状态的集合，是所有可能的观测状态的集合，即：

，

其中，M是隐状态的个数，N是观测状态的个数。

　　对于一个长度为T的序列，Y是对应的状态序列, X是对应的观测序列，即：

，

其中，。

        我们对这里提到的序列做些解释，在t时刻和t+1时刻的状态序列和观测序列分别是：

t 时刻：

t+1时刻：

它们之间有一个关系，也就是在t+1时刻只是在t时刻的基础上增加了状态和对应的观测值。因为只有经历了t时刻才能到达t+1时刻，然后才出现状态和对应的观察值。理解这一点对后面的理论证明会很有帮助。

---

观测序列生成机理

        观测序列生成机理指的是HMM在已知模型后，是如何一步步生成观测序列的。它有助于我们理解HMM为什么可以表示成形式。以上面的HMM模型表示图为例：

假设现在你站在的位置上，因为隐状态的初始分布式是已知的，而且隐状态到观测状态的概率也是已知的，所以此时你可沿着箭头方向向下走一步生成观测值，此时序列的第一个值已经生成，因为到的状态转移概率是已知的，此时可以得到的隐状态的概率，也就是你可以从走到，达到了之后，那么现在从走到就与从走到是类似的了，此时会生成第2个观测值，依次走下去，就可以生成整个观测序列了。下面使用案例按照这个思路具体来生成。

模型对应的隐状态初始分布，隐状态转移矩阵，观测状态矩阵分别如下：

	下雨	晴天
	0.6	0.4

小宝应该如下做出选择：

（1）第1天

根据如下公式来计算

最后一项中的项都是已知的，分别是观测状态概率和隐状态初始分布，如下：

P(x1=郊游)=P(郊游|晴天)P(晴天)+P(郊游|下雨)P(下雨)=0.6*0.4+0.1*0.6=0.3

同理，

P(x1=逛街)=0.3*0.4+0.4+0.6=0.36，

P(x1=游戏)=0.1*0.4+0.5+0.6=0.34

因为P(x1=逛街)概率最大，所以小宝第一天很可能会选择逛街。

（2）第2天

根据如下两步计算：

P(y2=晴天)=P(y2=晴天|y1=晴天)P(y1=晴天)+P(y2=晴天|y1=雨天)P(y1=雨天)

同理计算出P(y2=下雨)。

P(x2=郊游)=P(x2=郊游|y2=晴天)P(y2=晴天)+P(x2=郊游|y2=下雨)P(y2=下雨)

同理得到P(x2=逛街)和P(x2=游戏)，最后根据计算结果，做出活动选择。

（3）第3天

计算与第二天相同。

        以上HMM观测序列的生成思路，可以一般地如下叙述：

（1）生成x1

由初始分布F和观测矩阵G，得到第一个观测值x1，计算公式如下：

（2）生成（）

分为两步：

a、由转移矩阵Q和的状态概率分布Q生成的状态概率分布；

b、将的状态概率分布看成是初始分布，重复步骤（1）生成xi；

---

        接下来，我们来解决HMM的三大经典问题。

经典问题一之前向算法

问题：给定模型和观测序列，求？

解：为了方便起见，将简记为，在本经典问题求解过程中关于λ的条件概率也都如此简记。

        对于任意一个状态序列，可能出现的状态序列总共有个。这里先假设是其中一个。那么

上式最后一步是由观测独立性假设得到，即只与中的有关。同理将递推下去，最终得到

由隐状态转移矩阵和隐状态初始分布可以计算得到。

我们再来计算在隐状态序列Y下生成观测序列X的条件概率：

第2步由观测独立性假设，即观测值只与当前的状态有关。由观测矩阵可以得到。

有了和，我们就能计算X和Y的联合概率了，如下： 

那么最终就可以如下计算：

等式右边表示在各种可能的状态下（个），所以

到此就完成了的计算。

        下面对以上方法计算的复杂度做个简单说明。根据的计算公式，完成一个观测值的概率计算，需要计算个运算（计算每一个Y有2T个乘积，总共有的Y），使用大O表示就是复。这种暴力计算手段，计算复杂度随着T和N的增长成指数级增长，实际中根本无法计算。实际上，我们在<观测序列生成机理>一节使用的就是这种暴力方法。下面介绍另一种更简单的计算方法，称之为“前向算法”。

        假设在时刻t，状态为，观察值为的概率记为，称之为前向概率。现在假设我们已经找到了t时刻，所有可能状态下，观察值为的前向概率，现在我们使用递推法计算出在t+1时刻各个状态的前向概率，其中即：

记表示t时刻状态为，且t+1时刻状态为，观察序列为的概率，所以

       （由观测独立性假设得到）

                                   

这样我们就得到了和的递推关系。另外，递推关系的初始值，也就是t=1时刻的前向概率为：

这样有了前向概率的初始值和递推关系，就可以计算任意时刻t的前向概率了。

经典问题一中需要求的，其实就是在时刻T，观察到的概率，即：

       （1）

        下面对该算法的计算复杂度说明，我们先计算从到的计算量，即：

总共做个乘积和加法运算，那么从到就需要计算个乘积和加法运算，

再根据（1）式，总共需要计算，大O表示为。从复杂度看，比之前的暴力方法提升了很多。实际上，暴力方法是穷举法，前向概率是递推法。

 

经典问题二

略。

 

经典问题三之viterbi算法

问题：给定模型=（F，Q，G）和观测序列，预测最可能出现的隐状态序列。数学表达如下：

解：因为，已经给定，所以是常数，问题等价于找到使得联合概率最大即可。

下面结合图介绍viterbi算法，如图：

图中每个实心圆表示某个时刻可能出现的状态，每个方块表示对应的观测值。实心圆之间的箭头，表示隐状态转移，比如图中的红色箭头，表示t-1时刻状态Y1，在t时刻转移为状态Y2。

         我们注意到，任意一个状态序列正好与图中的一条路径一一对应，这条路径从t=1时刻状态为的实心圆开始，然后沿着箭头连接到t=2时刻状态为的实心圆，一直连接下去，直到t=T时刻状态为的实心圆。对应的这条路径记为。所以求解，其实就是从图中寻找一条最优路径使得联合概率最大。这是viterbi算法思想一。下面我们来寻找这样的路径。

        我们知道从时刻1到达时刻t总共有条不同路径，将它们根据时刻t的不同状态分为类，也就是在时刻t隐状态为的所有路径分为一类，时刻t到达状态的路径分为一类，等等，记类别分别为。现在从所有路径中寻找一条使得最大的最优路径问题就转化为从M个类中先分别找出一条使得最大的路径，然后再从这M条路径中找到使最大的路径。这样我们就将一个问题分解成了M个小问题。这是viterbi算法思想二。现在固定t时刻的状态，假设为，在类别中使达到最大的路径记为，最大概率记为。另外，我们还需要记录下此时的状态，也就是倒数第二个节点的状态，记为，即。为了书写方便，引用之前的记号

，

根据的定义，它可以如下表示：

同理t+1时刻对应的，如下表示：

下面推导和两者的关系，注意到与无关，只与有关，所以

   （2）

等式（2）两边先对变量求最大值，然后对变量求最大值：

                            （3）

最后一项最大值是从下面这些值中选取：

这样和递归就建立起来了。

这个递归说明：如果我们已经找到了从时刻1到时刻t的所有可能状态对应的最大概率，这个概率乘以转移概率，然后求得它们乘积中的最大值，最后再乘以观测概率，也就找到了从时刻1到时刻t+1状态为的最大概率。可以用如下图表示：

最优路径就是概率乘积值最大的那条路径。假设它们中的最大者是，那么现在我们至少能够确定最优的路径的最后两个节点，分别是和。最优路径中前面这些节点如何找到呢？事实上，上面的递推公式（3）隐含了一个性质：

的最优路径的前t个节点组成的路径是对应的最优路径。因为是的最优路径，所以公式（3）简化为

当状态i和j固定后，和成正比，那么就是的最优路径，如果不是，假设的最优路径是，那么路径将是的最优路径，矛盾。

 

基于上面这些介绍，我们们使用记录的状态往回追溯就可以找出最优路径。具体如下：

（1）使得最大，所以就是t+1时刻的状态；

（2）记录了在t+1时刻时，第t个节点的状态，就是这个节点的状态，记作；

（3）的值记录的就是在t时刻，t-1时刻的状态，记作

...

按照递归可以追溯到t=1时刻的状态，也就能得到

 

viterbi算法基本思路：

（1）由初始时的和递推公式，计算出任意时刻t的，同时记录前一个节点的状态;

（2）找到中的最大者，它对应的路径就是我们要找的，此时可以得到最后两个节点状态i和；

（3）使用记录的前一个状态，回溯出所有时刻的状态，得到

 

viterbi算法求解案例

下面我们以“小宝出行”案例来熟悉下vertibi算法。

（1）对于时刻t=1，也就是第一天，可能的状态为{下雨，晴天}，小宝第一天选择的是郊游，另外，从Start开始只有一条路径到达晴天，所以

(晴天)=P(x1=郊游，y1=晴天)=P(x1=郊游|y1=晴天)P(y1=晴天)=0.6*04=0.24

(下雨)=P(x1=郊游，y1=下雨)=P(x1=郊游|y1=下雨)P(y1=下雨)=0.1*0.6=0.06

因为第一天的前一天没有状态，所以不存在。

 

（2）对于时刻t=2，也就是第二天，小宝选择的是逛街，根据递推有：

，所以，

(晴天)=P(x2=逛街|y2=晴天)*max{P(y2=晴天|y1=晴天)(晴天)，P(y2=晴天|y1=下雨)(下雨)}

            =0.3*max{0.6*0.24，0.3*0.06}=0.3*max{0.144，0.018}=0.0432

(晴天)=晴天

同理，

(下雨)=P(x2=逛街|y2=下雨)*max{P(y2=下雨|y1=晴天)(晴天)，P(y2=下雨|y1=下雨)(下雨)}

             =0.4*max{0.4*0.24，0.7*0.06}=0.4*max{0.096，0.042}=0.0384

(下雨)=晴天

 

（3）对于时刻t=3，也就是第三天，小宝选择游戏，根据递推：

，所以，

(晴天)=P(x3=游戏|y3=晴天)*max{P(y3=晴天|y2=晴天)(晴天)，P(y3=晴天|y2=下雨)(下雨)}

             =0.1*max{0.6*0.0432，0.3*0.0384}=0.1*max{0.02592，0.01152}=0.002592

(晴天)=晴天

(下雨)=P(x3=游戏|y3=下雨)*max{P(y3=下雨|y2=晴天)(晴天)，P(y3=下雨|y2=下雨)(下雨)}

             =0.5*max{0.4*0.0432，0.7*0.0384}=0.5*max{0.01728，0.02688}=0.01344

(下雨)=下雨

 

下面开始回溯：

(下雨)>(晴天)，所以第3天下雨，而(下雨)=下雨，所以第二天也是下雨，根据(下雨)=晴天，所以第一天是晴天。

推算出3天天气是：晴天，下雨，下雨。

 

viterbi算法代码实现

import numpy as np


def viterbi(trans_prob, emit_prob, init_prob, views, states, obs):
    """
    viterbi算法

    :param trans_prob: 状态转移概率矩阵
    :param emit_prob: 观察概率矩阵，也称为发射概率矩阵
    :param init_prob: 初始状态分布
    :param views: 所有可能的观测值集合
    :param states: 所有可能的状态集合
    :param obs: 实际观测值序列
    :return:
    """

    state_num, obs_len = len(states), len(obs)
    delta = np.array([[0] * state_num] * obs_len, dtype=np.float64)
    phi = np.array([[0] * state_num] * obs_len, dtype=np.int64)
    print('state_num=', state_num, 'obs_len=', obs_len)
    print('delta=', delta)
    print('phi=', phi)
    # 初始化
    for i in range(state_num):
        delta[0, i] = init_prob[i] * emit_prob[i][views.index(obs[0])]
        phi[0, i] = 0
    print('初始化后delta=', delta)
    print('初始化后phi=', phi)

    # 递归计算
    for i in range(1, obs_len):
        for j in range(state_num):
            tmp = [delta[i - 1, k] * trans_prob[k][j] for k in range(state_num)]
            delta[i, j] = max(tmp) * emit_prob[j][views.index(obs[i])]
            phi[i, j] = tmp.index(max(tmp))

    # 最终的概率及节点
    max_prob = max(delta[obs_len - 1, :])
    last_state = int(np.argmax(delta[obs_len - 1, :]))

    # 最优路径path
    path = [last_state]
    for i in reversed(range(1, obs_len)):
        end = path[-1]
        path.append(phi[i, end])

    hidden_states = [states[i] for i in reversed(path)]

    return max_prob, hidden_states


def main():
    # 所有可能的状态集合
    states = ('晴天', '下雨')
    # 观测集合
    views = ['郊游', '逛街', '游戏']
    # 转移概率: Q -> Q
    trans_prob = [[0.6, 0.4],
                  [0.3, 0.7]]
    # 观测概率, Q -> V
    emit_prob = [[0.6, 0.3, 0.1],
                 [0.1, 0.4, 0.5]]
    # 初始概率
    init_prob = [0.4, 0.6]
    # 观测序列
    obs = ['郊游', '逛街', '游戏']

    max_prob, hidden_states = viterbi(trans_prob, emit_prob, init_prob, views, states, obs)
    print('最大的概率为: %.5f.' % max_prob)
    print('隐藏序列为：%s.' % hidden_states)


if __name__ == '__main__':
    main()

 

HMM模型应用

中文分词

 

股市分析