(Java) 算法——动态规划 最长公共子序列 图解
前言
遇到了用动态规划来求解最长公共子序列问题,算法这块儿比较薄弱,便想着在网上找现成的思路和代码,也算拾人牙慧,但有一点没想到,都已经22年了,关于LCS问题网上给出的答案如此一言难尽……,只有零散几篇对于新手来说比较友好,但也仅仅这样,好在自己花了点时间,勉强领悟了一番,写以成文,以便来时温故。
动态规划基本思想及要点
这块儿是看吴师兄学算法(公众号)文章摘录的
基本思想
动态规划算法与分治法类似,其基本思想就是将待求解问题分解成若干子问题,先求解子问题,然后从这些问题的解得到原问题的解。与分治法不同的是,适合动态规划求解的问题,经分解得到的子问题往往不是相互独立的。
在用分治法求解时,有些子问题被重复结算了很多次,如果我们能够保存已解决子问题的答案,在需要时找出已求得答案,这样就可以避免大量重复计算,可以用一个表来记录所有已解决子问题的答案,不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中,而这就是动态规划的思想。
小结
- 将待求解问题分成若干子问题,先求子问题,然后从这些子问题的解得到原问题的解
- 经分解得到的子问题往往不是相互独立的
- 保存已解决子问题的答案,避免重复计算
要点
如何判定一个问题是否可以用动态规划来解决,就需要掌握动态规划的两个基本要素,最优子结构性质和重叠子问题性质
最优子结构性质
当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。问题的最优子结构性质提供了该问题可用动态规划求解的重要线索。
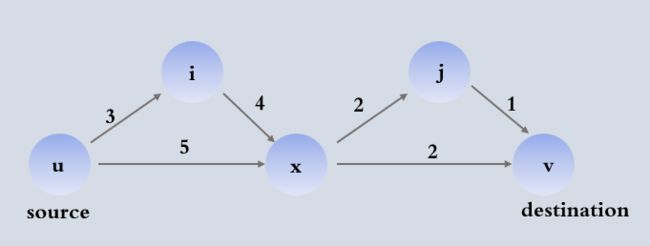
例如,最短路径问题有如下最优子结构:
结点x是从源结点u到目标结点v的最短路径上的节点,则源结点u到目标结点v的最短路径7就等于从源结点u到结点x的最短路径5加上从结点x到目标结点v的最短路径2的和。源结点u到目标结点v的最短路径就是要求解的最优解,源结点u到结点x的最短路径和从结点x到目标结点v的最短路径均为子问题的最优解,而问题的最优解包含了其子问题的最优解,则该问题具有最优子结构性质。
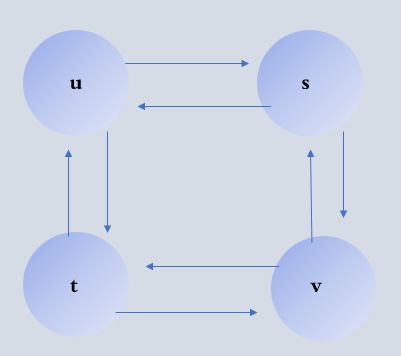
但最长路径问题就不具有最优子结构性质,注意这里的最长路径指的是从两个结点间的最长简单路径(即不存在环的路径)
从结点u到结点v有两条最长,分别为u——> s ——> v和u ——> t ——> v,但与最短路径问题不同,这些最长路径不具有最优子结构性质,比如,从结点u到结点v有两条最长路径u ——> s ——> v并不等于从u到s的最长路径u ——> t ——> v ——> s与从s到v的最长路径s ——> u ——> t ——> v的加和。
重叠子问题性质
简单讲就是子问题的解会被重复调用
LCS问题分析
字串与子序列
有图有真相
一个长度为n的序列,其子序列个数为2n-1,所以解决LCS问题最好不使用暴力搜索方法
分解
最长公共子序列问题分解成子问题根据已造轮子可知,设A=“a0、a1、……、am-1”,B=“b0、b1、……、bn-1”,Z=“z0、z1、……、zk-1”为它们最长公共子序列,不难证明有如下性质:
1). 如果am-1 = bn-1,则zk-1 = am-1=bn-1,简单讲就是A和B最后一个字符相等,那么这个字符肯定为最长公共子序列中的最后一个字符,于是就有“z0、z1、……、zk-2”是“a0、a1、……、am-2”和“b0、b1、……、bn-2”的一个最长公共子序列
2). 如果am-1!=bn-1,则若zk-1!=am-1,那么“z0、z1、……、zk-1”是“a0、a1、……、am-2”和“b0、b1、……、bn-1”的一个最长公共子序列
3). 如果am-1!=bn-1,则若zk-1!=bn-1,那么“z0、z1、……、zk-1”是“a0、a1、……、am-1”和“b0、b1、……、bn-2”的一个最长公共子序列
由此可以获得递推公式
dp数组推导(图解)
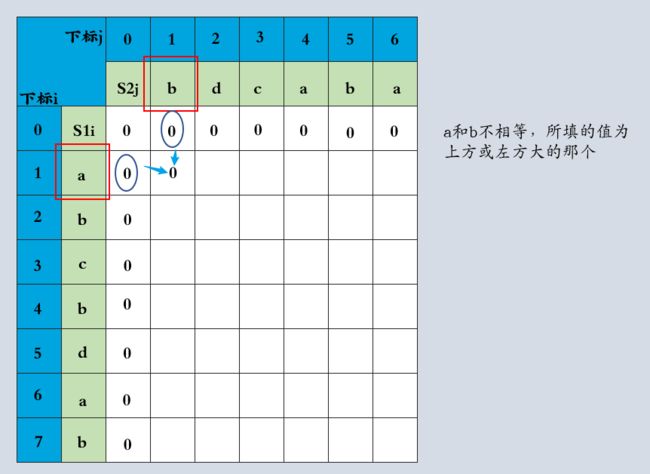
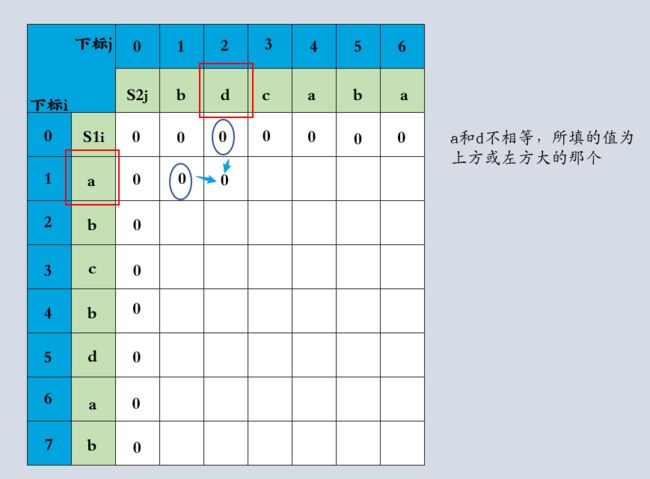
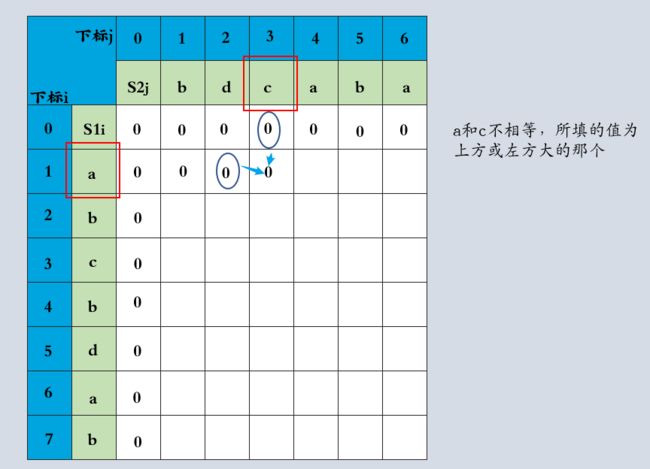
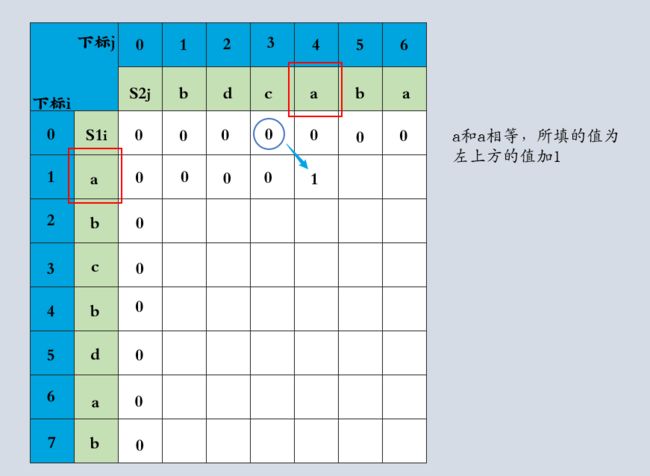
dp数组用于记录LCS长度,下面根据递归公式一行行进行推导


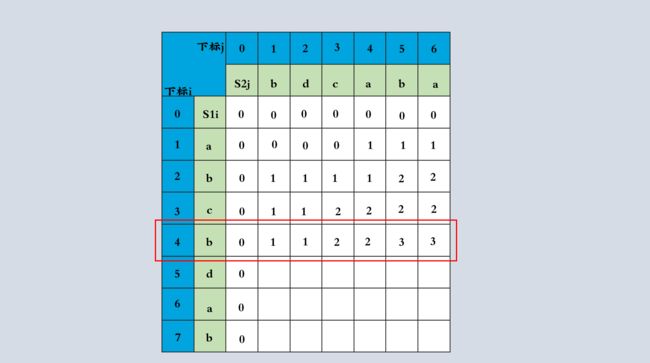
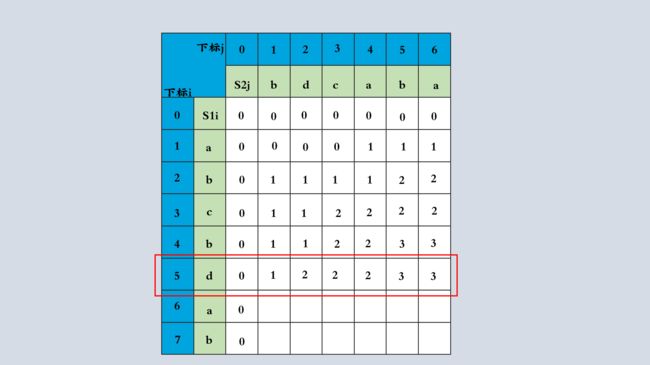
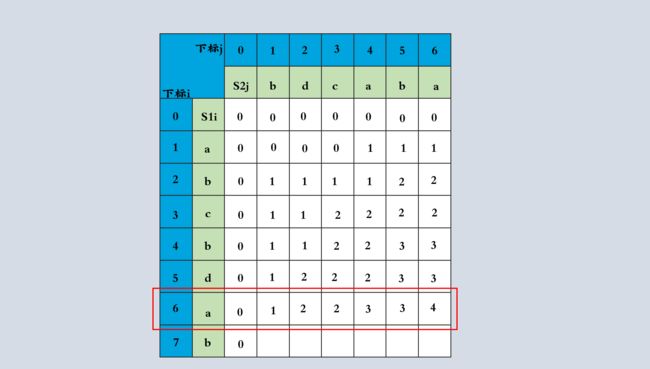

通过递推公式进行LCS长度推导这个过程,可以知道dp[i][j]是从三个方向推出的,分别是左上,向左,向上
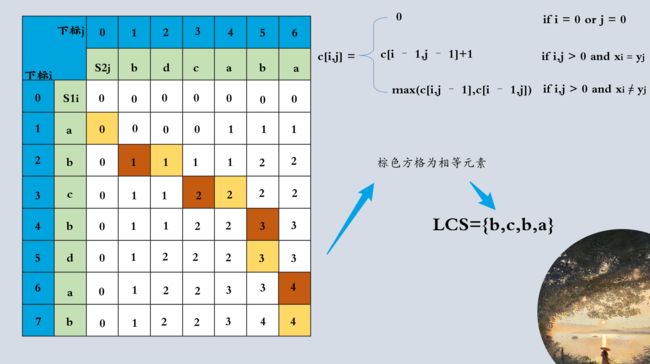
构造LCS(回溯)
得到dp数组后,为了得到LCS需要从dp[7][6]倒推出两序列共同元素,倒退有三种方向回溯
代码实现
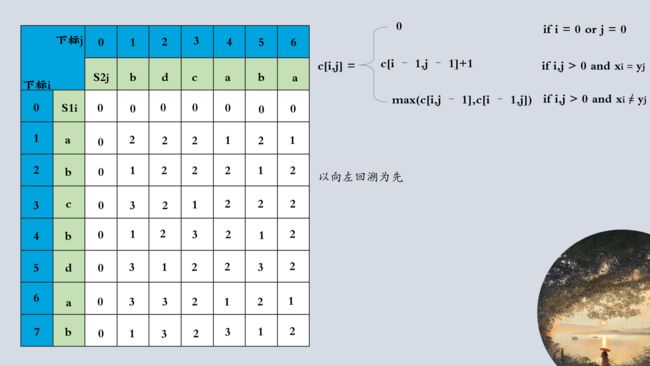
下面的代码为dp数组及回溯方向的实现(向左回溯为主)
package operation.dp;
public class LCSLD {
public static void LCS(int[][] dir, int [][] dp,String s1,String s2){
for(int i = 1;i <= s1.length();i++){
char c1 = s1.charAt(i - 1);
for(int j = 1;j <= s2.length();j++){
char c2 = s2.charAt(j - 1);
//开始列出状态方程
if (c1 == c2){
dp[i][j] = dp[i-1][j-1]+1;
dir[i][j] = 1; //来源左上方
}else{
if (dp[i][j-1] >= dp[i-1][j]){
dp[i][j] = dp[i][j-1];
dir[i][j] = 2; //来源左方
}
else{
dp[i][j] = dp[i-1][j];
dir[i][j] = 3; //来源上方
}
}
}
}
}
public static void LCSD(int [][] dir, int i, int j, String s1){
if(i== 0 || j == 0) {
return;
}
if(dir[i][j] == 1){
LCSD(dir,i - 1,j - 1,s1);
System.out.print(s1.charAt(i - 1));
}else{
if (dir[i][j] == 2)
LCSD(dir,i,j - 1,s1);
else
LCSD(dir,i - 1,j,s1);
}
}
}
下面的代码为dp数组及回溯方向的实现(向上回溯为主)
package operation.dp;
public class LCSFD {
public static void LCS(int[][] dir,int [][] dp,String s1,String s2){
for(int i = 1;i <= s1.length();i++){
char c1 = s1.charAt(i - 1);
for(int j = 1;j <= s2.length();j++){
char c2 = s2.charAt(j - 1);
if (c1 == c2){
dp[i][j] = dp[i-1][j-1]+1;
dir[i][j] = 1; //来源左上方
}else{
if(dp[i-1][j] >= dp[i][j-1]){
dp[i][j] = dp[i-1][j];
dir[i][j] = 2; //来源上方
}else{
dp[i][j] = dp[i][j-1];
dir[i][j] = 3; //来源左方
}
}
}
}
}
public static void LCSD(int [][] dir,int i,int j,String s1){
if(i == 0 || j ==0){
return;
}
if(dir[i][j] == 1){
LCSD(dir,i - 1,j - 1,s1);
System.out.print(s1.charAt(i - 1));
}else{
if(dir[i][j] == 2)
LCSD(dir,i - 1,j,s1);
else
LCSD(dir,i,j - 1,s1);
}
}
}
下面的代码为主程序代码
package operation.dp;
public class MainApp {
public static void main(String[] args) {
String s1 = "abcbdab";
String s2 = "bdcaba";
//先对dp数组做初始化操作
//Java中数组静态初始化在编译时就已完成,而动态初始化在运行时才完成,
//且动态初始化的初始值都为0
int [][] dp = new int[s1.length()+1][s2.length()+1]; //i+1行j+1列
int [][] dir = new int[s1.length()+1][s2.length()+1];
int [][] dp1 = new int[s1.length()+1][s2.length()+1]; //i+1行j+1列
int [][] dir1 = new int[s1.length()+1][s2.length()+1];
//开始时间
long stime = System.currentTimeMillis();
//以向左回溯为先
LCSLD.LCS(dir,dp,s1,s2);
System.out.println("dp数组如下:");
for(int i = 0;i <= s1.length();i++){
for(int j = 0;j <= s2.length();j++){
System.out.printf("%5d",dp[i][j]);
}
System.out.println();
}
System.out.println("回溯数组如下:");
for(int i = 0;i <= s1.length();i++){
for(int j = 0;j <= s2.length();j++){
System.out.printf("%5d",dir[i][j]);
}
System.out.println();
}
System.out.print("最长公共子序列为:");
LCSLD.LCSD(dir,s1.length(),s2.length(),s1);
System.out.println();
//以向上回溯为先
LCSFD.LCS(dir1,dp1,s1,s2);
System.out.println("回溯数组如下:");
for(int i = 0;i <= s1.length();i++){
for(int j = 0;j <= s2.length();j++){
System.out.printf("%5d",dir1[i][j]);
}
System.out.println();
}
System.out.print("最长公共子序列为:");
LCSFD.LCSD(dir1,s1.length(),s2.length(),s1);
System.out.println();
//结束时间
long etime = System.currentTimeMillis();
System.out.printf("执行时长: %d 毫秒",(etime - stime));
}
}
待解决问题
经过上述努力,发现LCS回溯的方向可以说是一根筋儿,这样就导致结果不全,以上述例子来说,LCS总共有三个,结果只能输出两个,暂时只能到这儿了,以后看看有没有机会实现
参考
主要是看了四篇文章有所启迪,一篇CSDN上的、一篇博客园上的、一篇公众号上的、一篇个人博客上的
小结
好的算法讲解真的很重要,可以事半功倍,就目前接触而言,代码随想录的算法讲解很不错(对新手友好且免费),其他成体系成专栏的讲解(暂时没有发现,可能都在自己的一亩三分地下)希望多多涌现,这样后来者学习算法就可以站在前人肩上前行了,也许时代造就了现在的社会氛围较为着急,很难静下心来公益的分享知识,所以不能一味归咎于个人(机构)老是搞钱,等中国的科技素养追赶上了中国的科技水平,那时候也许环境不会这么苛责,现在如果每个人认真发一份光,其实也可以燎原,不需要等待那天到来,说通透点就是,我花个一天时间把这个问题弄通透,然后分享出来,你花一天时间把那个问题弄通透分享出来,那么对于第三方来说在这两个问题就可以少走较小弯路了,当然,这说的也可能扯淡,不好把握全局,不好定性脉络,认知差信息差总是提醒着我,多走几步,再回头观望那时的想法是否正确