NLP基础:n-gram语言模型和神经网络语言模型
文章目录
- 语言模型的计算
-
- n-gram 语言模型
- n-gram 平滑技术
- 神经网络语言模型(NNLM)
-
- 基本思想
- 神经网络语言模型小结
- 语言模型评价指标—困惑度
语言模型是自然语言处理中的重要技术,假设一段长度为 T T T的文本中的词依次为 w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w1,w2,…,wT,语言模型将计算该序列的概率:
P ( w 1 , w 2 , … , w T ) . P(w_1, w_2, \ldots, w_T). P(w1,w2,…,wT).
语言模型有助于提升自然语言处理任务的效果,例如在语音识别任务中,给定一段“厨房里食油用完了”的语音,有可能会输出“厨房里食油用完了”和“厨房里石油用完了”这两个读音完全一样的文本序列。合适的语言模型能够判断出前者的概率大于后者的概率,于是可以得到正确的“厨房里食油用完了”这个文本序列。
语言模型的计算
我们可以把文本看作一段离散的时间序列 w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w1,w2,…,wT,假设每个词是按时间先后顺序依次生成的,那么在离散的时间序列中, w t w_t wt( 1 ≤ t ≤ T 1 \leq t \leq T 1≤t≤T)可看作在时间步(time step) t t t的输出或标签。于是,对于一个句子而言,有:
P ( w 1 , w 2 , … , w T ) = ∏ t = 1 T P ( w t ∣ w 1 , … , w t − 1 ) . P(w_1, w_2, \ldots, w_T) = \prod_{t=1}^T P(w_t \mid w_1, \ldots, w_{t-1}). P(w1,w2,…,wT)=t=1∏TP(wt∣w1,…,wt−1).
例如,一段含有4个词的文本序列的概率:
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) P ( w 4 ∣ w 1 , w 2 , w 3 ) . P(w_1, w_2, w_3, w_4) = P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_1, w_2, w_3). P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3).
n-gram 语言模型
如果一个句子特别长,那么计算和存储多个词共同出现的概率的复杂度会呈指数级增加。
由此引入 n-gram 语言模型,n-gram 是一种基于统计模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为n的滑动窗口操作,形成了长度为n的字节片段序列,每一个字节片段称为gram。
n-gram 模型基于马尔可夫假设,第n个词的出现只与前面 n-1 个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积:
P ( w 1 , w 2 , … , w T ) ≈ ∏ t = 1 T P ( w t ∣ w t − ( n − 1 ) , … , w t − 1 ) . P(w_1, w_2, \ldots, w_T) \approx \prod_{t=1}^T P(w_t \mid w_{t-(n-1)}, \ldots, w_{t-1}) . P(w1,w2,…,wT)≈t=1∏TP(wt∣wt−(n−1),…,wt−1).
这些概率可以通过直接从语料中统计 n 个词同时出现的次数得到。常用的是 n=2 的Bi-Gram和 n=3 的Tri-Gram。
例如,长度为4的序列 w 1 , w 2 , w 3 , w 4 w_1, w_2, w_3, w_4 w1,w2,w3,w4在Bi-Gram和Tri-Gram中的概率分别为:
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 2 ) P ( w 4 ∣ w 3 ) , P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) P ( w 4 ∣ w 2 , w 3 ) . \begin{aligned} P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_2) P(w_4 \mid w_3) ,\\ P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_2, w_3) . \end{aligned} P(w1,w2,w3,w4)P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3),=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w2,w3).
当 n n n较小时, n n n元语法往往并不准确。然而,当 n n n较大时, n n n元语法需要计算并存储大量的词频和多词相邻频率。
对于Bi-Gram而言,有:
p ( w t ∣ w t − 1 ) = c ( w t − 1 , w t ) ∑ w t c ( w t − 1 , w t ) p(w_t|w_{t-1}) = \frac{c(w_{t-1},w_t)}{\sum_{w_t}c(w_{t-1},w_t)} p(wt∣wt−1)=∑wtc(wt−1,wt)c(wt−1,wt)
当 t = 1 t=1 t=1时,为了使上式有意义,在句子的开头加上 < B O S >
用计算最大似然估计的方法计算概率:
p ( w i ∣ w i − 1 ) = c ( w i − 1 w i ) ∑ w i c ( w i − 1 w i ) p(w_i|w_{i-1}) = \frac{c(w_{i-1}w_i)}{\sum_{w_i}c(w_{i-1}w_i)} p(wi∣wi−1)=∑wic(wi−1wi)c(wi−1wi)
其中,函数 c 表示个数统计。
用计算最大似然估计的方法计算概率 p ( B R O W R E A D A B O O K ) p(BROW \quad \quad READ \quad A \quad BOOK) p(BROWREADABOOK),具体过程如下:
P ( B R O W ∣ < B O S > ) = c ( < B O S > B R O W ) ∑ w c ( < B O S > w ) = 1 3 P ( R E A D ∣ B R O W ) = c ( B R O W R E A D ) ∑ w c ( B R O W w ) = 1 1 P ( A ∣ R E A D ) = c ( R E A D A ) ∑ w c ( R E A D w ) = 2 3 P ( B O O K ∣ A ) = c ( A B O O K ) ∑ w c ( A w ) = 1 2 P ( < E O S > ∣ B O O K ) = c ( B O O K < E O S > ) ∑ w c ( B O O K w ) = 1 2 \begin{aligned} &P(BROW |
所以:
p ( B R O W R E A D A B O O K ) = P ( B R O W ∣ < B O S > ) × P ( R E A D ∣ B R O W ) × P ( A ∣ R E A D ) × P ( B O O K ∣ A ) × P ( < E O S > ∣ B O O K ) = 1 3 × 1 × 2 3 × 1 2 × 1 2 ≈ 0.06 \begin{aligned} &p(BROW \; READ\; A\; BOOK)\\ = &P(BROW |
n-gram 平滑技术
在自然语言处理处理中,难免会遇到未登录词(OOV),即测试集中出现了训练集中未出现过的词,或者未出现过的子序列,导致语言模型计算出的概率为0。使用平滑技术的目的就是在条件概率为0时,防止整个句子的概率为0,人为按一定规则,给0条件概率一定的值。常见的平滑方法有:
- 加法平滑方法
- 古德-图灵(Good-Turing)估计法
- Katz平滑方法
- Jelinek-Mercer平滑方法
- Witten-Bell平滑方法
- 绝对减值法
具体内容参考宗成庆老师的《统计自然语言处理 第二版》
神经网络语言模型(NNLM)
基本思想
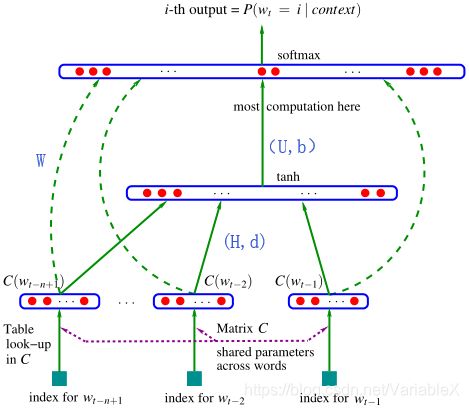
神经网络语言模型先给每个词赋予一个词向量,利用神经网络去建模当前词出现的概率与其前 n-1 个词之间的约束关系,即通过神经网络去学习词的向量表示。结构如下图所示:
具体而言,假设当前词出现的概率只依赖于前 n − 1 n-1 n−1个词。即:
p ( w t ∣ w 1 … w t − 1 ) = p ( w t ∣ w t − n + 1 … w t − 1 ) p(w_t|w_1\ldots w_{t-1}) = p(w_t|w_{t-n+1}\ldots w_{t-1}) p(wt∣w1…wt−1)=p(wt∣wt−n+1…wt−1)
假设 V V V表示所有N个词的集合, w t ∈ V w_t \in V wt∈V,存在一个 ∣ V ∣ × m |V|\times m ∣V∣×m的参数矩阵C,矩阵的每一行代表每一个词的特征向量,m代表每个特征向量由m个维度。 C ( w t ) C(w_t) C(wt)表示第 t 个词 w t w_t wt的对应的特征向量。
如上图所示,将句子的前 n-1 个词特征对应的向量 C ( w t − n + 1 ) … C ( w t − 1 ) C(w_{t-n+1})\ldots C(w_{t-1}) C(wt−n+1)…C(wt−1)作为神经网络的输入,输出当前的词是 w t w_t wt的概率。计算过程如下:
y = W x + U t a n h ( d + H x ) + b y = W x + U tanh(d+Hx) + b y=Wx+Utanh(d+Hx)+b
其中:
x = ( C ( w t − 1 ) , C ( w t − 2 ) , … , C ( w t − n + 1 ) ) x = (C(w_{t-1}),C(w_{t-2}),\ldots ,C(w_{t-n+1})) x=(C(wt−1),C(wt−2),…,C(wt−n+1))
经过上式得到 y w = ( y w , 1 , y w , 2 , … , y w , N ) T y_w = (y_{w,1},y_{w,2},\ldots,y_{w,N})^T yw=(yw,1,yw,2,…,yw,N)T ,其中,将 y w y_w yw进行softmax后, y w , i y_{w,i} yw,i 表示当上下文为 c o n t e x t ( w ) context(w) context(w)时,下一个词恰好是词典中第 i i i个词的概率,即:
P ( w ∣ c o n t e x t ( w ) ) = e y w , i w ∑ i = 1 N e y w , i P(w|context(w)) = \frac{e^{y_{w,i_w}}}{\sum_{i=1}^N e^{y_{w,i}}} P(w∣context(w))=∑i=1Neyw,ieyw,iw
其中, i w i_w iw表示词在词典中的索引。
计算集中在隐藏层和输出层之间的矩阵向量运算,以及输出层上的softmax归一化运算。该模型的参数是:
θ = ( b , d , W , U , C ) \theta = (b,d,W,U,C) θ=(b,d,W,U,C)
损失函数是:
L = − 1 T ∑ t log p ^ ( w t = i ∣ w t − n + 1 … w t − 1 ) + R ( θ ) L = -\frac{1}{T} \sum_t \log \hat p(w_t=i|w_{t-n+1}\ldots w_{t-1}) + R(\theta) L=−T1t∑logp^(wt=i∣wt−n+1…wt−1)+R(θ)
$ R(\theta)$是正则化项,用于控制过拟合。
有了损失函数,我们可以用梯度下降法,在给定学习率 η \eta η的条件下,进行参数更新:
θ ← θ − η ∂ L ∂ θ \theta \leftarrow \theta - \eta \frac{\partial L}{\partial \theta} θ←θ−η∂θ∂L
直至收敛,得到一组最优参数。
神经网络语言模型小结
只要词的表征足够好,就能具有比 n-gram 更好的泛化能力,从而很大程度地降低了数据稀疏带来的问题。不足之处是仅包含了有限的前文信息。
优点:(1) 长距离依赖,具有更强的约束性;(2) 避免了数据稀疏所带来的OOV问题;(3) 好的词表征能够提高模型泛化能力。
缺点:(1) 模型训练时间长;(2) 可解释性较差。
神经网络语言模型与 n-gram 模型相比,
1,相似的词具有相似的向量。对 n-gram 模型而言,如果语料中S1=“A dog is running in the room”出现了10000次,而S2=“A cat is running in the room”只出现了1次,p(S1)肯定会远大于p(S2)。而实际上,dog 和 cat 是相似的存在,神经网络语言模型所得到的词向量距离会比较近,表示两个词十分相似。
2,用向量表示的词自带平滑化功能(由p(w∣Context(w))∈(0,1)p(w|Context(w))∈(0,1)p(w∣Context(w))∈(0,1)不会为零),不再需要像 n-gram 那样进行额外处理了。
语言模型评价指标—困惑度
通常用困惑度作为语言模型的评价指标。
设存在文本序列 W = ( w 1 , w 2 , … , w N ) W=(w_1,w_2,\ldots,w_N) W=(w1,w2,…,wN),则每个词的平均交叉熵为:
H ( W ) = − 1 N log P ( w 1 , w 2 , … , w N ) H(W) = -\frac{1}{N}\log P(w_1,w_2,\ldots,w_N) H(W)=−N1logP(w1,w2,…,wN)
显然,交叉熵越小,得到的概率模型越接近真实分布,进一步我们定义困惑度为:
P r e p l e x i t y ( W ) = 2 H ( W ) = 1 P ( w 1 , w 2 , … , w N ) N Preplexity(W) = 2^{H(W)} = \sqrt[N]{\frac{1}{ P(w_1,w_2,\ldots,w_N)}} Preplexity(W)=2H(W)=NP(w1,w2,…,wN)1
由公式可知:困惑度越小,说明所建模的语言模型越精确。
参考文章
-
A Neural Probabilistic Language Model
-
深入理解语言模型 Language Model
-
6.1语言模型
-
语言模型基础