AutoML 与 Bayesian Optimization 概述
1. AutoML 概述
AutoML是指对于一个超参数优化任务(比如规定计算资源内,调整网络结构找到准确率最高的网络),尽量减少人为干预,使用某种学习机制,来调节这些超参数,使得目标问题达到最优。
这些学习机制包括最基本的
- Grid Search
- Random Search
也有比较传统的
- 贝叶斯优化
- 多臂老虎机(multi-armed bandit)
还有比较新颖的
- 进化算法
- 强化学习
在AutoML中有一个分支专注于自动学习深度神经网络的网络架构,叫做Neural architecture search (NAS),当下分类网络中效果最好的EfficientNets就是这个领域的产物。
2. Bayesian Optimization
2.1 Grid Search & Random Search
神经网络训练是由许多超参数决定的,例如网络深度,卷积类型,卷积核大小,channel数量等等。为了找到一个好的超参数组合,最直观的想法就是Grid Search,其实也就是对离散化的参数取值进行穷举搜索
不同于传统AutoML相关的问题,比如决策树相关的RandomForest,GBDT等。对于NAS领域,随着网络越来越复杂,超参数也越来越多,要想将每种可能的超参数组合都实验一遍(即Grid Search)明显不现实。
另一种比较朴素的想法是进行随机搜索,但显然也不是一种高效的策略。
2.2 Bayesian Optimization
贝叶斯优化是一种近似逼近的方法,用一个代理函数来拟合超参数与模型评价结果之间的关系,在每次迭代中,采集函数 根据当前代理函数的反馈选择最有潜力的超参数进行实验。实验得到了一组真实的超参数-模型评价结果的pair对,将这个结果喂回给代理函数进行修正,如此反复迭代,期望其在过程中以更高的效率找到比较好的超参数组合。
上面介绍的是贝叶斯优化中最简单的一种形式Sequential model-based optimization (SMBO),这段描述中涉及了3个概念:
- 代理函数
代理函数本质上就是一个概率模型,对超参数与模型效果背后对应的黑箱映射关系进行建模。
常用的代理函数有高斯过程,高斯混合模型,还有基于树的模型,比如回归随机森林
首先,我们用f代表超参数与模型效果背后对应的真实映射关系
我们用代理函数,记为模型M,来建模f代表的映射关系。
也就是通过已知的采样数据集D,拟合模型M,来得到一个近似表达f的概率模型
FITMODEL(M,D) -> p(y|x, D)
在后面的介绍中,都假设f服从高斯过程,也就是使用高斯过程作为代理函数
即f~GP(μ,K)。(GP:高斯过程,μ:均值,K:协方差kernel)。
所以预测也是服从正态分布的,即有p(y|x,D)=N(y|μ,σ^2)
- 采集函数
采集函数被用来根据当前的代理函数,选出本次迭代要尝试的超参数。
采集函数的选择有许多种,包括Probability of improvement、Expected improvement、Entropy search、 Upper confidence bound等。
这里给出Expected improvement的详细定义
假设f′=minf,这个f′表示目前已知的f的最小值。
utility function定义如下(代表超参数为x时的收益/提升):
u(x)=max(0,f′−f(x))
Expected improvement的含义是收益/提升的期望
因此 EI(x) = E[u(x)|x,D]
当带入我们的假设,即f服从高斯过程时,EI的计算公式如下

于是遍寻所有的超参数取值x,便可以通过采集函数获取本次迭代需要尝试的超参数。
- exploitation-and-exploration (利用与探索)
在学习贝叶斯优化的过程中,我思考了两个问题:
Grid Search & Random Search 不是很高效的结论很容易接受,究其根本原因是什么?
为什么不直接选择能够使代理函数取最优值的超参数组合,还要使用采集函数呢?
我发现很多资料使用exploitation-and-exploration的概念对此进行了解释。
上面两个问题,代表了搜索过程中的两种极端。
第一个问题,即 Random Search 对应了exploration,搜索过程只是一味的在探索位置区域,并没有对已经获得的信息进行任何的利用。
第二个问题,如果我们直接使用代理函数对应的概率模型进行搜索,对应了exploitation,即充分的对已知信息进行挖掘利用,但是缺乏对位置超参数区域的探索。
因此我们需要在利用与探索之间,进行一些权衡,来达到更高的搜索效率和更好的搜索结果。
Expected improvement这个采集函数就能很好的体现这一点,我们回到它的公式

当均值μ(x)较小时,EI(x)取值会因为左式较大而增大
当协方差K(x,x)较大时,EI(x)取值会因为右式较大而增大
μ(x)较小对应的是已经探索过的点中哪些比较好的超参数组合
K(x,x)较大对应的是那些为探索过的区域
因此,Expected improvement 公式从原理上对exploitation-and-exploration进行了很好权衡,当发现了一个点结果不错时,会更倾向于在它附近进行深入挖掘,但同时这个邻域内的点的方差不断变小,采集函数又会去探索那些完全未知的区域。
观察下面两幅图可以更直观的感受一下。其中蓝色曲线是要拟合的函数,红色点是已经探索过的采样点,橙色曲线对应在这些采样点上学习出来的概率模型的均值,浅蓝色阴影是置信区间。

3. Bayesian Optimization 练习
为了更好的学习贝叶斯优化的使用,这里做了一个练习。
首先,我选择的是scikit- optimization库的ask-and-tell方法实现我的贝叶斯优化器。
使用peaks函数加上一些随机噪声来作为待优化的目标函数。函数定义如下:
def cost_function(x, y):
z = 3 * (1-x)**2 * np.exp(-(x**2) - (y+1)**2) \
- 10 * (x/5 - x**3 - y**5) * np.exp(-x**2 - y**2) \
- 1/3 * np.exp(-(x+1)**2 - y**2) + np.random.randn()
return z
函数可视化如下:

编写 Bayesian Optimization 寻优代码如下:
# -*- coding: utf-8 -*-
"""
Created on Fri Oct 11 20:55:06 2019
skopt(Scikit Optimize) 练习1
使用ask-and-tell的流程来模拟进行超参数的优化
@author: zyb_as
"""
from mpl_toolkits.mplot3d import Axes3D
import imageio
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
def cost_function(x, y):
z = 3 * (1-x)**2 * np.exp(-(x**2) - (y+1)**2) \
- 10 * (x/5 - x**3 - y**5) * np.exp(-x**2 - y**2) \
- 1/3 * np.exp(-(x+1)**2 - y**2) + np.random.randn()
return z
def transform_coordinate2index(coordinate, interval=0.01):
index = int((coordinate + 3)/interval)
return index
# 计算目标函数Z(用于画图)
interval = 0.01
x=np.arange(-3, 3, interval)
y=np.arange(-3, 3, interval)
X, Y = np.meshgrid(x, y)
Z = np.zeros(X.shape)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
xij = X[i][j]
yij = Y[i][j]
Z[i][j] = cost_function(xij, yij)
# 绘制目标函数
fig = plt.figure()
ax = Axes3D(fig)
plt.xlabel('x')
plt.ylabel('y')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
ax.view_init(elev=-50.,azim=270)
plt.savefig('peaks.png')
plt.show()
# 计算理论最优值,用于判断优化效果
min_z = np.min(Z)
min_idx = np.where(Z==min_z)
x_min_idx = int(min_idx[1])
y_min_idx = int(min_idx[0])
# define the skopt optimizer
import skopt
opt = skopt.Optimizer(
[
skopt.space.Real(-3.0, 3.0, name='x'),
skopt.space.Real(-3.0, 3.0, name='y'),
],
n_initial_points=5,
base_estimator='GP',
acq_func='EI',
acq_optimizer='auto',
random_state=0,
)
cmap = mpl.cm.get_cmap('jet', 1000) # color map
images = []
total_epochs = 100
point_x_list = []
point_y_list = []
best_cost = 1e100
best_hyperparams = None
for i in range(total_epochs):
fig = plt.figure()
plt.imshow(Z, cmap=cmap)
# plot the hyperparams find before
plt.scatter(point_x_list, point_y_list, s=30, c='slategray')
# plot the theoretical best hyperparams
plt.scatter(x_min_idx, y_min_idx, s=50, c='white')
# ask a new hyperparams
cur_hyperparams = opt.ask()
# use the hyperparams to train the model
# ...
# evaluate the cost
cur_cost = cost_function(cur_hyperparams[0], cur_hyperparams[1])
print(i+1, cur_cost, cur_hyperparams)
find_new_best = False
if cur_cost < best_cost:
best_cost = cur_cost
best_hyperparams = cur_hyperparams
print('find new best hyperparams')
find_new_best = True
# tell the optimizer the cost
opt.tell(cur_hyperparams, cur_cost)
# 绘制本次超参的位置
new_x_list = []
new_y_list = []
new_x = transform_coordinate2index(cur_hyperparams[0])
new_y = transform_coordinate2index(cur_hyperparams[1])
new_x_list.append(new_x)
new_y_list.append(new_y)
point_x_list.append(new_x)
point_y_list.append(new_y)
if find_new_best:
plt.scatter(new_x_list, new_y_list, s=100, c='black')
else:
plt.scatter(new_x_list, new_y_list, s=30, c='black')
# 显示
plt.savefig('temp.png')
plt.close()
#plt.show()
# 记录一帧图像
images.append(imageio.imread('temp.png'))
# 生成gif图
imageio.mimsave('GP_rand5.gif', images, duration=0.5)
使用高斯过程作为代理函数的优化过程可视化如下:(前5次随机,共迭代100次,进行了3次实验均能收敛到最优值附近)
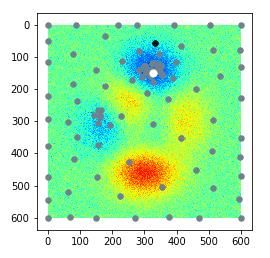
图中,白点是全局最优值,当前迭代的采样点显示为黑色,如果当前采样点是历史最优值,会进行放大显示。(图片大小原因gif图没传上来,只能放个静态图片在这里,感兴趣可以运行下代码看下具体效果)
使用随机森林作为代理函数(前5次随机,共迭代100次),进行了3次实验只有一次收敛到最优值附近),优化过程分别可视化如下:
实验1:成功

实验2:失败

实验3:失败
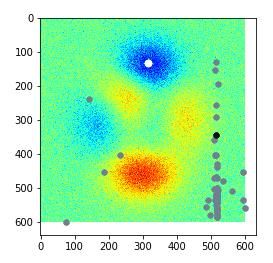
通过实验,我发现,在低维问题的优化中,高斯过程要比基于树模型的代理函数好用。有材料提到像随机森林,GBDT这样的树模型在高维空间中的表现要好很多(这个我没有验证)。
此外,随机森林这类的模型有个突出优势,就是能够处理离散输入,这使得在很多情况下它是唯一选择。
因此,我又修改了下代码,尝试让RF在本实验上的效果大幅提升。
思路是使用RandomForest+Random结合的方式进行并行的搜索。每次搜索3个点,一个点使用采集函数获得,两个点进行随机,然后将3个点的采样值都喂回给RF进行学习,这样就很好的解决了RF不喜欢探索未知区域,进而无法寻找到最优值的问题。
改进的代码如下:
# -*- coding: utf-8 -*-
"""
Created on Mon Oct 14 15:51:56 2019
skopt(Scikit Optimize) 练习3
练习2的优化版本
使用RandomForest+Random结合的方式进行并行的策略搜索
RF模型结合随机,试图解决RF模型探索未知区域能力差的缺点
@author: zyb_as
"""
from mpl_toolkits.mplot3d import Axes3D
import imageio
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
def cost_function(x, y):
z = 3 * (1-x)**2 * np.exp(-(x**2) - (y+1)**2) \
- 10 * (x/5 - x**3 - y**5) * np.exp(-x**2 - y**2) \
- 1/3 * np.exp(-(x+1)**2 - y**2) + np.random.randn()
return z
def transform_coordinate2index(coordinate, interval=0.01):
index = int((coordinate + 3)/interval)
return index
# 计算目标函数Z(用于画图)
interval = 0.01
x=np.arange(-3, 3, interval)
y=np.arange(-3, 3, interval)
X, Y = np.meshgrid(x, y)
Z = np.zeros(X.shape)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
xij = X[i][j]
yij = Y[i][j]
Z[i][j] = cost_function(xij, yij)
# 计算理论最优值,用于判断优化效果
min_z = np.min(Z)
min_idx = np.where(Z==min_z)
x_min_idx = int(min_idx[1])
y_min_idx = int(min_idx[0])
# define the skopt optimizer
import skopt
opt = skopt.Optimizer(
[
skopt.space.Real(-3.0, 3.0, name='x'),
skopt.space.Real(-3.0, 3.0, name='y'),
],
n_initial_points=1,
base_estimator='RF', # can choose "GP", "RF", "ET", "GBRT"
acq_func='EI',
acq_optimizer='auto',
random_state=0,
)
# use these api as a random augment polices loader
rand_opt = skopt.Optimizer(
[
skopt.space.Real(-3.0, 3.0, name='x'),
skopt.space.Real(-3.0, 3.0, name='y'),
],
n_initial_points=1e10,
base_estimator='RF', # no matter to choose what value
acq_func='EI',
acq_optimizer='auto',
random_state=3, # better to be different with opt's random_state
)
cmap = mpl.cm.get_cmap('jet', 1000) # color map
images = []
total_epochs = 30
point_x_list = []
point_y_list = []
best_cost = 1e100
best_hyperparams = None
parallel_level = 3
for i in range(total_epochs):
fig = plt.figure()
plt.imshow(Z, cmap=cmap)
# plot the hyperparams find before
plt.scatter(point_x_list, point_y_list, s=30, c='slategray')
# plot the theoretical best hyperparams
plt.scatter(x_min_idx, y_min_idx, s=50, c='white')
# ask for a list of new hyperparams
rand_hyperparams_list = rand_opt.ask(parallel_level - 1)
new_hyperparams = opt.ask()
new_hyperparams_list = rand_hyperparams_list
new_hyperparams_list.append(new_hyperparams)
# parallel distribute tasks
cost_list = []
for parallel_index in range(parallel_level):
cur_hyperparams = new_hyperparams_list[parallel_index]
# use the hyperparams to train the model
# ...
# evaluate the cost
cur_cost = cost_function(cur_hyperparams[0], cur_hyperparams[1])
print("epoch{}_parallel{}".format(i+1, parallel_index+1), cur_cost, cur_hyperparams)
cost_list.append(cur_cost)
if cur_cost < best_cost:
best_cost = cur_cost
best_hyperparams = cur_hyperparams
print('find new best hyperparams')
# tell the optimizer the cost
for parallel_index in range(parallel_level):
opt.tell(new_hyperparams_list[parallel_index], cost_list[parallel_index])
rand_opt.tell(new_hyperparams_list[parallel_index], cost_list[parallel_index])
# 绘制本次并行探索的超参的位置
new_x_list = []
new_y_list = []
for parallel_index in range(parallel_level):
cur_hyperparams = new_hyperparams_list[parallel_index]
new_x = transform_coordinate2index(cur_hyperparams[0])
new_y = transform_coordinate2index(cur_hyperparams[1])
new_x_list.append(new_x)
new_y_list.append(new_y)
point_x_list.append(new_x)
point_y_list.append(new_y)
plt.scatter(new_x_list, new_y_list, s=30, c='black')
# 显示
plt.savefig('temp.png')
plt.close()
#plt.show()
# 记录一帧图像
images.append(imageio.imread('temp.png'))
# 生成gif图
imageio.mimsave('parallel_randRF_rand5.gif', images, duration=1)
改进后的效果如下:
可以看到,改进的效果还是挺明显的,对于exploitation-and-exploration有了很好的权衡。
借助 Bayesian Optimization 自动搜索数据增强方法的探索
借鉴Insight研究员的一个工作:
AutoML数据增广
GitHub
我探索了使用 Bayesian Optimization 自动搜索数据增强方法的实验。
在上面工作的基础上,我主要做了如下的修改:
1 将代理任务的网络由一个5层CNN改为mobilenet。
这样做虽然明显提高了整个算法搜索过程的耗时,但是单个评估实验的结论会更可靠,基于mobilenet的规模,也不至于使得搜索过程的耗时完全不可接受。
2 对架构进行修改,使其支持并行训练
实际使用中经常面临可用的gpu资源比较零碎,要想提高实验速度,需要解决多卡多机器的问题。
因此我对程序框架进行了修改,采用单服务端,多客户端的模式。服务端负责学习贝叶斯优化器,并根据学习结果分发任务给客户端;客户端领任务,对收到的数据增强组合进行评估,然后把结果返回给服务端。并且简化了使用过程,仅需要修改一个类似如下的配置文件:

这个实验由于比较消耗资源,有很多细节需要实验和调整,暂时还没有得到很好的成果。再加上最近又出了PBA,Fast AutoAugment,RandAugment这三篇自动搜索数据增强方法的paper,个人认为更有价值去研究,毕竟时间有限,本实验对应的这种思路后面可能就不再继续跟进了。
不过我感觉这个尝试还是很有意义的,因为这份代码可以作为一个autoML的通用并行框架使用,稍微改改就可以跑其它任务。
整个项目的代码整理到了我维护的AI工具箱中,具体位置bayesian-autoaugment,感兴趣的小伙伴可以看看
参考文献
写作本文阅读的资料及文中部分配图出自以下地址:
AutoML数据增广
AutoML总结
贝叶斯优化(Bayesian Optimization)深入理解
机器学习贝叶斯超参数优化
贝叶斯优化(BayesianOptimization)
Bayesian Optimization Primer