【读点论文】FBNetV3: Joint Architecture-Recipe Search using Predictor Pretraining 网络结构和超参数全当训练参数给训练了
FBNetV3:使用预测器预训练的联合体系结构-配方搜索
Abstract
- 神经结构搜索(NAS)产生了最先进的神经网络，其性能优于最好的手动设计的对应物。然而，先前的NAS方法在一组训练超参数(即，训练方案)下搜索架构，忽略了更好的架构-方案组合。为了解决这个问题，本文提出了神经架构-方法搜索(NARS ),以同时搜索(a)架构和(b)它们相应的训练方法。
- NARS利用一个准确性预测器，对架构和训练配方进行联合评分，指导样本选择和排名。此外，为了补偿扩大的搜索空间，本文利用“free”架构统计数据(例如，FLOP count)来预训练预测器，从而显著提高其采样效率和预测可靠性。在通过约束迭代优化训练预测器之后，本文在仅仅几分钟的CPU时间内运行快速进化搜索来为各种资源约束生成architecturerecipe对，称为FBNetV3。
- FBNetV3构成了一系列最先进的compact neural networks，其性能优于自动和手动设计的竞争对手。例如，FBNetV3的EfficientNet和ResNeSt精度与ImageNet相当，但FLOPs分别减少了2.0倍和7.1倍。此外，FBNetV3显著提高了下游对象检测任务的性能，改善了mAP，而且与基于EfficientNet的同类产品相比，FLOPs减少了18%,参数减少了34%。
- FBNet系列论文是由Facebook推出的NAS算法搜索到的网络，V1、V2采用的是和DARTS一样的方法，通过构建Supernet和微分梯度方法计算出最佳的网络；V3采用的是自己独特的方法——JointNAS，将超参数和训练策略都作为搜索空间，通过粗粒度和细粒度两个stage搜索出来最好的网络和训练参数。
- 论文地址：[2006.02049] FBNetV3: Joint Architecture-Recipe Search using Predictor Pretraining (arxiv.org)
Introduction
-
设计高效的计算机视觉模型是一个具有挑战性但重要的问题:从自动驾驶汽车到增强现实的无数应用都需要高度精确的compact models——即使在功率、计算、内存和延迟方面受到限制。可能的约束和架构组合的数量非常大，使得手工设计几乎不可能。
-
尽管NAS在网路架构方面取得了非常好的结果，比如EfficientNet、MixNet、MobileNetV3等等。但无论基于梯度的NAS，还是基于super net的NAS，亦或基于强化学习的NAS均存在这几个缺陷
- 忽略了训练超参数，即仅仅关注于网络架构而忽略了训练超参数的影响；
- 仅支持一次性应用，即在特定约束下只会输出一个模型，不同约束需要不同的模型。
-
，作者提出了JointNAS，同时对网络架构与训练策略进行搜索，将网络架构与对应的训练策略通过NAS联合搜索，之前的NAS方法主要聚焦在网络架构，而没有在意网络性能验证时的训练参数的设置是否合适，这可能导致模型性能下降，而JointNAS可以在资源约束的情况下，搜索 最 准 确 的 训 练 参 数 以 及 网 络 结 构 \textcolor{red}{最准确的训练参数以及网络结构} 最准确的训练参数以及网络结构。
-
作为解决方案，最近的工作采用神经架构搜索(NAS)来设计最先进的高效深度神经网络。NAS的一个类别是可区分神经架构搜索(DNAS)。这些路径搜索算法是高效的，通常在训练一个网络所需的时间内完成一次搜索。然而，DNAS不能搜索对模型性能至关重要的非架构超参数。此外，基于超网的NAS方法受到搜索空间的限制，因为整个超图必须适合内存以避免缓慢的收敛[Proxylessnas]或paging。
-
其他方法包括强化学习(RL) [MnasNet]和进化算法(ENAS) [Large-scale evolution of image classifiers]。然而，这些方法都有几个缺点:
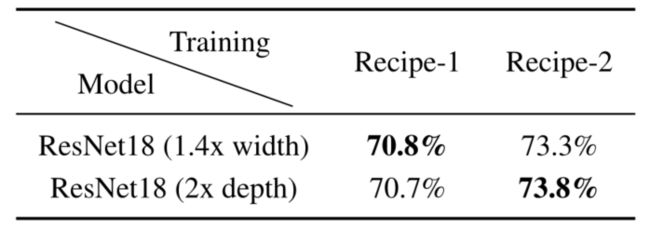
- Ignore training hyperparameters:顾名思义，NAS只搜索架构，而不搜索相关的训练超参数(即“训练方法”)。这忽略了一个事实， 即 不 同 的 训 练 方 法 可 能 会 极 大 地 改 变 一 个 架 构 的 成 败 \textcolor{red}{即不同的训练方法可能会极大地改变一个架构的成败} 即不同的训练方法可能会极大地改变一个架构的成败，甚至改变架构的排名(下表)。
-
-
不同的训练配方可以改变架构的等级。ResNet18 1.4x倍宽度和2倍深度分别指1.4倍宽度和2.0倍深度缩放因子的ResNet18。训练配方详情见附录A.1。
-
- Support only one-time use:许多传统的NAS方法 为 一 组 特 定 的 资 源 约 束 产 生 一 个 模 型 \textcolor{red}{为一组特定的资源约束产生一个模型} 为一组特定的资源约束产生一个模型。这意味着部署到一系列产品时，每个产品都有不同的资源限制，需要为每个资源设置重新运行一次NAS。或者，模型设计者可以搜索一个模型，并使用手动试探法对其进行次优缩放，以适应新的资源约束。
- Prohibitively large search space to search:在搜索空间中天真地包括训练配方要么是不可能的(DNAS，基于超网的NAS)，要么是极其昂贵的，因为训练仅架构的准确度预测器在计算上已经是昂贵的(RL，ENAS)。
- Ignore training hyperparameters:顾名思义，NAS只搜索架构，而不搜索相关的训练超参数(即“训练方法”)。这忽略了一个事实， 即 不 同 的 训 练 方 法 可 能 会 极 大 地 改 变 一 个 架 构 的 成 败 \textcolor{red}{即不同的训练方法可能会极大地改变一个架构的成败} 即不同的训练方法可能会极大地改变一个架构的成败，甚至改变架构的排名(下表)。
-
为了克服这些挑战，本文提出了Neural Architecture-Recipe Search(NARS)来解决上述限制。本文的见解有三个方面:
- (1)为了支持NAS结果在多个资源约束下的重用，本文训练了一个准确性预测器，然后使用该预测器在几分钟的CPU时间内为新的资源约束找到architecturerecipe对。
- (2)为了避免仅架构或仅配方搜索的陷阱，该预测器同时对训练配方和架构评分。
- (3)为了避免预测器训练时间的禁止性增长，本文在代理数据集上预训练预测器，以根据架构表示来预测架构统计(例如，FLOPs，#参数)。
-
在顺序执行预测器预训练，约束迭代优化和基于预测器的进化搜索后，NARS产生了可概括的训练配方和紧凑的模型，在ImageNet上获得了最先进的性能，超过了所有现有的手动设计或自动搜索的神经网络。本文的贡献总结如下:
- Neural Architecture-Recipe Search: 提出了一个预测器，它联合评分训练配方和架构，第一次联合搜索，在训练配方和架构上，以 设 计 者 的 知 识 为 尺 度 \textcolor{blue}{设计者的知识为尺度} 设计者的知识为尺度。
- Predictor pretraining: 为了能够在这个更大的空间上进行有效的搜索，本文进一步提出了一种预训练技术，显著提高了预测器的采样效率。
- Multi-use predictor: 本文的预测器可以用于快速进化搜索，在几分钟内快速生成各种资源预算的模型。
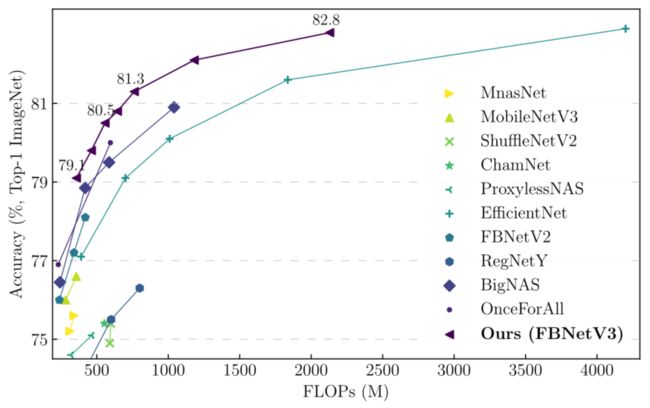
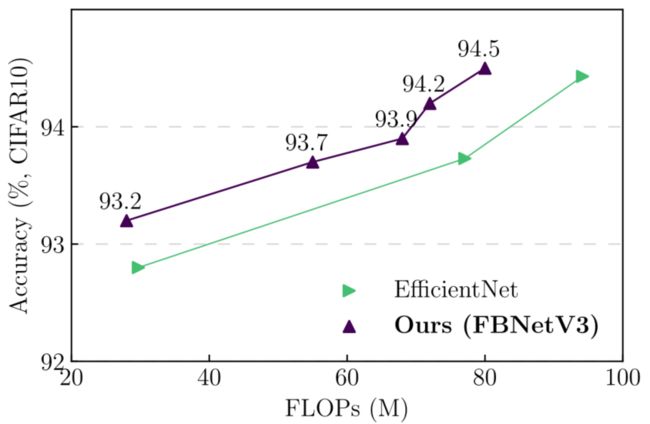
- State-of-the-art ImageNet accuracy：每FLOP的ImageNet精度达到了最高水平。例如，如下图所示，本文的FBNetV3和efficientnet相当的精度时，比efficientnet少49.3%的FLOPs,如下图所示。
-
-
ImageNet精度与模型FLOPs fbnet v3与其他高效卷积神经网络的比较。FBNetV3以557M (2.1G) FLOPs实现了80.8% (82.8%)的顶级精度，为精度-效率权衡设置了新的SOTA。
-
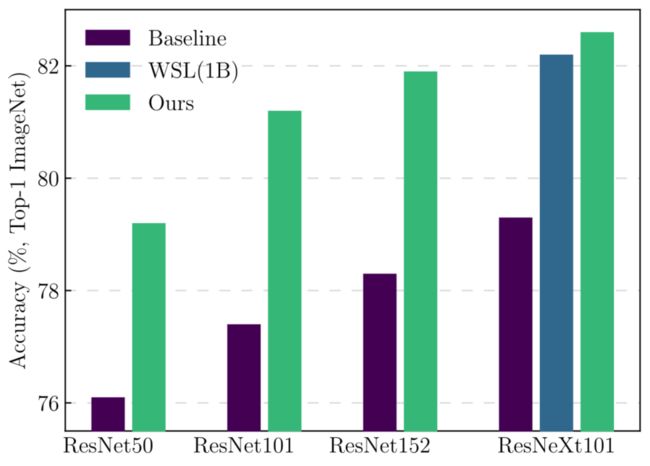
- Generalizable training recipe:NARS的单一方法搜索在各种神经网络中获得了显著的精度增益，如下图所示。本文的ResNeXt101-32x8d实现了82.6%的顶级精度；这甚至超过了在1B额外图像上训练的弱监督对手[Exploring the limits of weakly supervised pretraining]。
-
-
使用搜索到的训练配方提高现有架构的准确性。WSL指的是使用1B附加图像的弱监督学习模型。
-
-
网 络 架 构 与 训 练 策 略 同 时 进 行 搜 索 \textcolor{red}{网络架构与训练策略同时进行搜索} 网络架构与训练策略同时进行搜索。这是之前的方法所并未尝试的一个点，之前的方法主要聚焦在网络架构，而训练方法则是采用比较常规的一组训练方式。
-
FBnetV3将网络架构与对应的训练策略通过NAS联合搜索。在ImageNet数据集上，FBNetV3取得了媲美EfficientNet与ResNeSt性能的同时具有更低的FLOPs(1.4x and 5.0x fewer)；更重要的是，该方案可以跨网络、跨任务取得一致性的性能提升。
Related work
- 紧凑型神经网络的工作始于手工设计，可分为架构性和非架构性修改。
Manual architecture design:
- 大多数早期的工作都压缩了现有的架构。一种方法是修剪[Deep compression，NeST，Once for all: Train one network and specialize it for efficient deployment，Dreaming to distill: Data-free knowledge transfer via deepinversion]，其中层或通道根据某些试探法被移除。然而，修剪要么只考虑一个架构[Learning both weights and connections for efficient neural network]，要么只能顺序搜索越来越小的架构[NetAdapt]。这限制了搜索空间。
- 其他工作从头开始设计新的架构，使用成本友好的新操作。这包括卷积变体，如MobileNet中的深度方向卷积；MobileNetV2中的反转残差块；激活，如MobileNetV3中的hswish；以及像移位[Shift: A zero FLOP, zero parameter alternative to spatial convolutions]和通道混洗[shufflenet]这样的操作。虽然其中许多仍然用于最先进的神经网络，但手动设计的结构已经被自动搜索的结构所取代。
Non-architectural modifications:
- 许多网络压缩技术包括低位量化[Deep compression]到少至两位[Trained ternary quantization]甚至一位[Binarized neural networks]。其他工作下采样输入不均匀[Squeezeseg，Squeezesegv3，Efficient segmentation]以减少计算成本。
- 这些方法可以与架构改进相结合，以大致额外减少延迟。其他非架构修改涉及超参数调优，包括预深度学习时代的调优库[Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures]。几个深度学习专用的调优库也被广泛使用[Tune: A research platform for distributed model selection and training]。一类新的方法自动搜索数据扩充策略的最佳组合。这些方法使用策略搜索[Autoaugment]、基于人口的训练[Population based augmentation: Efficient learning of augmentation policy schedules]、基于贝叶斯的增强[A bayesian data augmentation approach for learning deep models]或贝叶斯优化[Neural architecture search with bayesian optimisation and optimal transport]。
Automatic architecture search:
- NAS自动化神经网络设计，实现一流的性能。几种最常见的NAS技术包括强化学习[Neural architecture search with reinforcement learning，MnasNet]，进化算法[Large-scale evolution of image classifiers，Regularized evolution for image classifier architecture search，Cars: Continuous evolution for efficient neural architecture search]和DNAS [Darts，Fbnet，V2，Single path one-shot neural architecture search with uniform sampling，SNAS: Stochastic neural architecture search]。
- DNAS用很少的计算资源快速训练，但是由于内存的限制而受到搜索空间大小的限制。一些工作试图解决这个问题，通过一次只训练子集[Proxylessnas]或通过引入近似值[Fbnetv2]。然而，它的灵活性仍然比不上竞争对手的强化学习方法和进化算法。反过来，这些先前的工作仅搜索模型架构[Progressive neural architecture search，Neural predictor for neural architecture search，Neural architecture search using deep neural networks and monte carlo tree search，Once for all: Train one network and specialize it for efficient deployment]或者在小规模数据集(例如，CIFAR) 上执行神经架构配方搜索。
- 相比之下，本文的NARS在ImageNet上联合搜索建筑和训练方法。为了弥补更大的搜索空间，本文(a)引入预测器预训练技术，以提高预测器的收敛速度,( b)采用基于预测器的进化搜索，在任何资源约束设置下，只需几分钟的CPU时间即可设计出架构接收对——显著优于进化搜索前预测器的最高排序候选。
- 本文还注意到先前的工作，即在一次搜索后生成一系列成本可忽略或为零的模型[Single path one-shot neural architecture search with uniform sampling，Cars: Continuous evolution for efficient neural architecture search，Nsganetv2: Evolutionary multi-objective surrogate-assisted neural architecture search]。
Method
-
本文的目标是找到最准确的架构和训练方法组合，以避免像以前的方法那样忽略架构配方对。然而，搜索空间通常组合起来很大，不可能进行彻底的评估。为了解决这个问题，本文训练一个准确度预测器，该预测器接受架构和训练配方表示。为此，本文采用了一个三阶段流水线(算法1):
- (1)使用架构统计对预测器进行预训练，从而显著提高其精度和采样效率。
- (2)使用约束迭代优化来训练预测器。
- (3)对于每组资源约束，仅在CPU时间内运行基于预测器的进化搜索，以产生高精度的架构-配方对。
-
JointNAS，分粗粒度和细粒度两个阶段，对网络架构和训练超参都进行搜索。
-
粗粒度阶段(coarse-grained)，该阶段主要迭代式地寻找高性能的候选网络结构-超参数对以及训练准确率预测器。
-
- 粗粒度搜索生成准确率预测器和一个高性能候选网络集, 这 个 预 测 器 是 一 个 多 层 感 知 器 构 成 的 小 型 网 络 \textcolor{green}{这个预测器是一个多层感知器构成的小型网络} 这个预测器是一个多层感知器构成的小型网络，包含了两个部分，一个代理预测器（Proxy Predictor），一个是准确率预测器（Accuracy Predictor）
- 预测器的结构如下图所示，包含一个结构编码器以及两个head，分别为辅助的代理head以及准确率head。代理head预测网络的属性(FLOPs或参数量等)，主要在编码器预训练时使用，准确率head根据训练参数以及网络结构预测准确率，使用代理head预训练的编码器在迭代优化过程中进行fine-tuned。
- Neural Acquisition Function，即预测器，见上图。它包含编码架构与两个head：
- （1）Auxiliary proxy head用于预训练编码架构、预测架构统计信息（比如FLOPs与参数两）。注：网络架构通过one-hot方式进行编码；
- （2）精度预测器，它接收训练策略与网路架构，同时迭代优化给出架构的精度评估。
- Early-stopping，作者还引入一种早停策略以降低候选网络评估的计算消耗；
- Predictor training，得到候选网络后，作者提出训练50个epoch同时冻结嵌入层，然后对整个模型再次训练50个epoch。作者采用Huber损失训练该精度预测器。该损失有助于使模型避免异常主导现象(prevents the model from being dominated by outliers)。
- Neural Acquisition Function，即预测器，见上图。它包含编码架构与两个head：
-
细粒度阶段(fine-grained stages)，借助粗粒度阶段训练的准确率预测器，对候选网络进行快速的进化算法搜索，该搜索集成了论文提出的超参数优化器AutoTrain。
-
-
Predictor
-
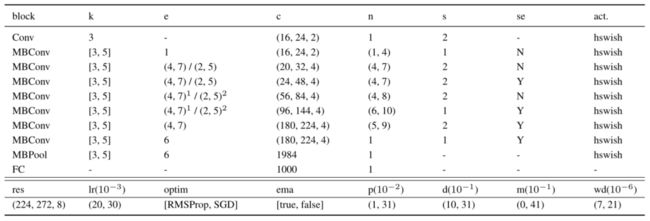
本文的预测器旨在预测给定架构和训练配方表示的准确性。使用one-hot分类变量(例如，对于块类型)和最小-最大归一化连续值(例如，对于通道计数)对架构和训练配方进行编码。参见下表中的完整搜索空间。
-
-
本文实验中的网络结构配置和搜索空间。MBConv、MBPool、k、e、c、n、s、se和act。
-
分别参考逆残差块[MobilenetV2]、efficient last stage[MobilenetV3]、核大小、扩展、#通道、#层数、步幅、挤压-激励、激活函数。res、lr、optim、ema、p、d、m和wd分别指分辨率、初始学习率、优化器类型、EMA、dropout率、随机深度dropout概率、mixup率和权重衰减。
-
EMA：指数移动平均（Exponential Moving Average）也叫权重移动平均（Weighted Moving Average），是一种给予近期数据更高权重的平均方法。
- 假设我们有n个数据： [ θ 1 , θ 2 , θ 3 , . . . , θ n ] [θ_1,θ_2,θ_3,...,θ_n] [θ1,θ2,θ3,...,θn].平均数为 v ˉ = 1 n ∑ i = 1 n θ i \bar{v}=\frac{1}{n}\sum_{i=1}^n\theta_i vˉ=n1∑i=1nθi.
- EMA: v t = β ⋅ v t − 1 + ( 1 − β ) ⋅ θ t v_t=β·v_{t-1}+(1-β)·θ_t vt=β⋅vt−1+(1−β)⋅θt，其中 v t v_t vt表示前 t 部分的平均值，β为加权权重值（一般为0.9~0.999）,v0=0
- 当 β = n − 1 n β=\frac{n-1}{n} β=nn−1时，EMA与普通的平均数两式形式上相等。
-
上面讲的是广义的ema定义和计算方法，特别的，在深度学习的优化过程中， θ t θ_t θt 是t时刻的模型权重weights， v t v_t vt是t时刻的影子权重（shadow weights)。在梯度下降的过程中，会一直维护着这个影子权重，但是这个影子权重并不会参与训练。基本的假设是，模型权重在最后的n步内，会在实际的最优点处抖动，所以取最后n步的平均，能使得模型更加的鲁棒。
-
-
实际使用中，如果令 v 0 = 0 v_0=0 v0=0，步数较少的情况下，ema的计算结果会有一定偏差。
-
理想的平均是绿色的，因为初始值为0，所以得到的是紫色的。因此可以加一个偏差修正（bias correction）。
-
v t = v t 1 − α t v_t=\frac{v_t}{1-\alpha^t} vt=1−αtvt
-
显然，当t很大时，修正近似于1。
-
-
令第n时刻的模型权重（weights）为 v n v_n vn，梯度为 g n g_n gn，可得：
- θ n = θ n − 1 − g n − 1 = θ n − 2 − g n − 1 − g n − 2 = θ 1 − ∑ i = 1 n − 1 g i θ_n=θ_{n-1}-g_{n-1}\\ =θ_{n-2}-g_{n-1}-g_{n-2}\\ =θ_{1}-\sum_{i=1}^{n-1}g_{i} θn=θn−1−gn−1=θn−2−gn−1−gn−2=θ1−i=1∑n−1gi
-
令第n时刻EMA的影子权重为 v n v_n vn ，可得：
-
v n = α v n − 1 + ( 1 − α ) θ n = α ( α v n − 2 + ( 1 − α ) θ n − 1 ) + ( 1 − α ) θ n = α n v 0 + ( 1 − α ) ( θ n + α θ n − 1 + α 2 θ n − 2 + . . . + α n − 1 θ 1 ) 代 入 上 面 θ n 的 表 达 ， 令 v 0 = θ 1 展 开 上 面 的 公 式 ， 可 得 ： v n = θ 1 − ∑ i = 1 n − 1 ( 1 − α n − i ) g i v_n=\alpha{v_{n-1}}+(1-\alpha)\theta_n\\ =\alpha(\alpha{v_{n-2}}+(1-\alpha)\theta_{n-1})+(1-\alpha)\theta_n\\ =α^nv_0+(1-α)(θ_n+αθ_{n-1}+α^2θ_{n-2}+...+α^{n-1}θ_{1})\\ 代入上面 θ_n 的表达，令 v_0=θ_1 展开上面的公式，可得：\\ v_n=θ_1-\sum_{i=1}^{n-1}(1-α^{n-i})g_i vn=αvn−1+(1−α)θn=α(αvn−2+(1−α)θn−1)+(1−α)θn=αnv0+(1−α)(θn+αθn−1+α2θn−2+...+αn−1θ1)代入上面θn的表达，令v0=θ1展开上面的公式，可得：vn=θ1−i=1∑n−1(1−αn−i)gi
-
EMA对第i步的梯度下降的步长增加了权重系数 1 − α n − i 1-α^{n-i} 1−αn−i ，相当于做了一个learning rate decay。
-
-
-
斜线左边的扩展用于阶段中的第一个块，而右边的扩展用于其余块。括号中的三元组代表最低值、最高值和步长；二值元组意味着步长为1，括号中的元组表示搜索过程中所有可用的选择。请注意，如果optim选择SGD，lr将乘以4。
-
具有相同上标的架构参数在搜索期间共享相同的值。
-
-
预测器结构是一个多层感知器(下图),由几个完全连接的层和两个头组成:
-
(1)一个辅助“代理”头，用于预训练编码器，从结构表示中预测结构统计(例如，FLOPs和#Parameters );
-
(2)精度头，在约束迭代优化中微调，从架构和训练配方的联合表示中预测精度。
-
-
预训练以预测架构统计数据(上图)。训练从架构-配方对预测准确性(底部)
-
Stage 1: Predictor pretraining
- 训练准确度预测器在计算上可能是昂贵的，因为每个训练标签表面上是在特定训练配方下完全训练的架构。为了减轻这一点，本文的解决方案是首先对代理任务进行预训练。预训练步骤可以帮助预测器形成输入的良好内部表示，从而减少所需的精度结构配方样本的数量。这可以显著降低所需的搜索成本。
- 为了构造一个用于预训练的代理任务，可以使用“free”的架构标签源:也就是说，像FLOPs和参数数量这样的架构统计数据。在这个预训练步骤之后，本文转移预训练的嵌入层来初始化精度预测器(见上图)。这将显著提高最终预测器的样本效率和预测可靠性。例如，为了达到相同的预测均方误差(MSE ),经过预训练的预测器只需要比未经预训练的预测器少5倍的样本，如下图(e)所示。因此，预测器预训练大大降低了整体搜索成本。
-
-
(a)和(b):预测器在代理度量上的性能，©和(d):预测器在有和没有预训练的准确性上的性能，(e):预测器的MSE与有和没有预训练的样本数的关系。
-
Stage 2: Training predictor
-
在此步骤中，本文训练预测器并生成一组high-promise候选项。如前所述，本文的目标是在给定的资源限制下找到最准确的架构和训练方法组合。因此，本文将架构搜索公式化为约束优化问题:
-
max ( A , h ) ∈ Ω a c c ( A , h ) s . t . g i ( A ) ≤ C i , i = 1 , . . . , γ ( 1 ) \max\limits_{(A,h)\inΩ}~acc(A,h)\\ s.t.~g_i(A)\leq{C_i},i=1,...,γ~(1) (A,h)∈Ωmax acc(A,h)s.t. gi(A)≤Ci,i=1,...,γ (1)
-
其中A、h和Ω分别指神经网络架构、训练配方和设计的搜索空间。acc将架构和训练方法映射到准确性。gi(A)和γ是指资源约束的公式和计数，如计算成本、存储成本和运行时延迟。
-
Constrained iterative optimization:
-
本文首先使用准蒙特卡罗(QMC) [Random number generation and quasiMonte Carlo methods]抽样来从搜索空间生成架构-配方对的样本池。然后，迭代地训练预测器:本文的(a)通过基于预测精度选择有利候选的子集来缩小候选空间，(b)使用early-stopping试探法来训练和评估候选，以及©使用 H u b e r 损 失 \textcolor{blue}{Huber损失} Huber损失来微调预测器。候选空间的这种迭代收缩避免了不必要的评估并提高了探索效率。
-
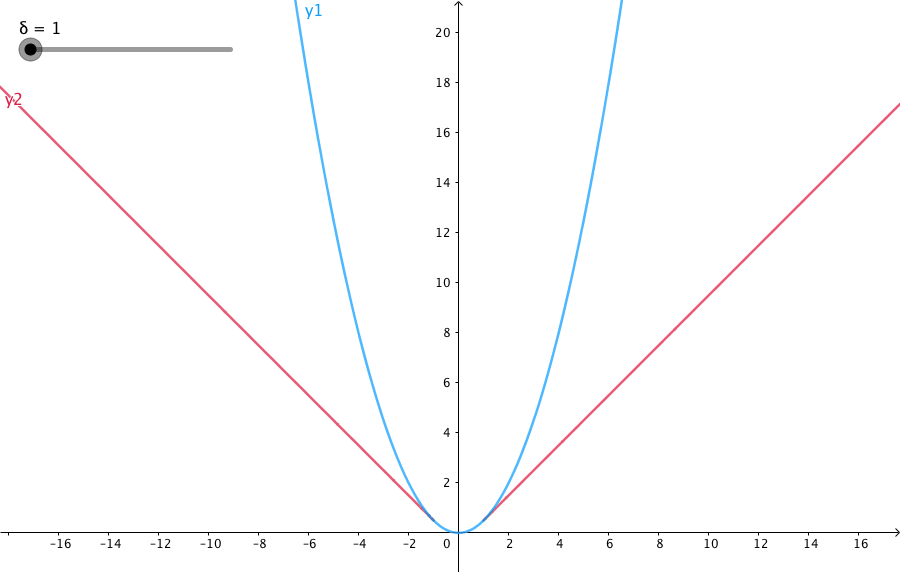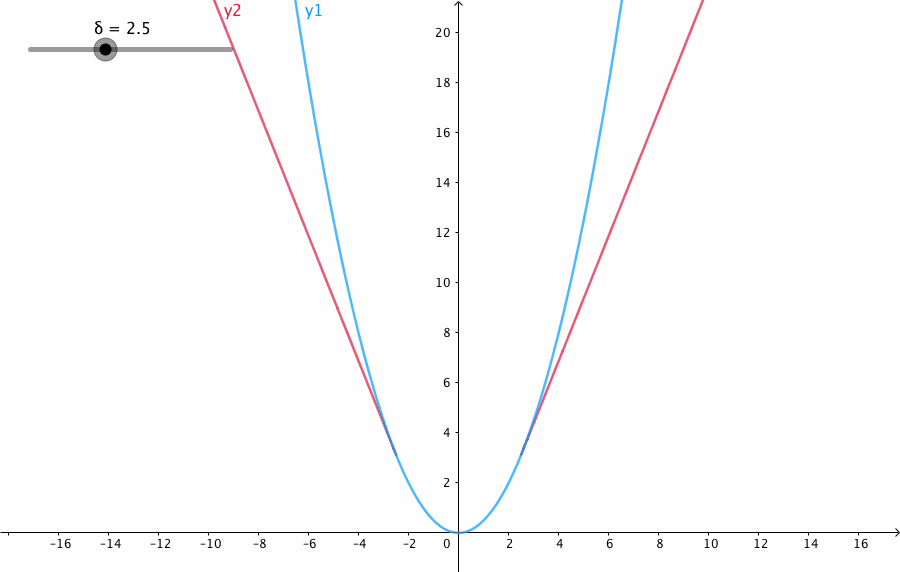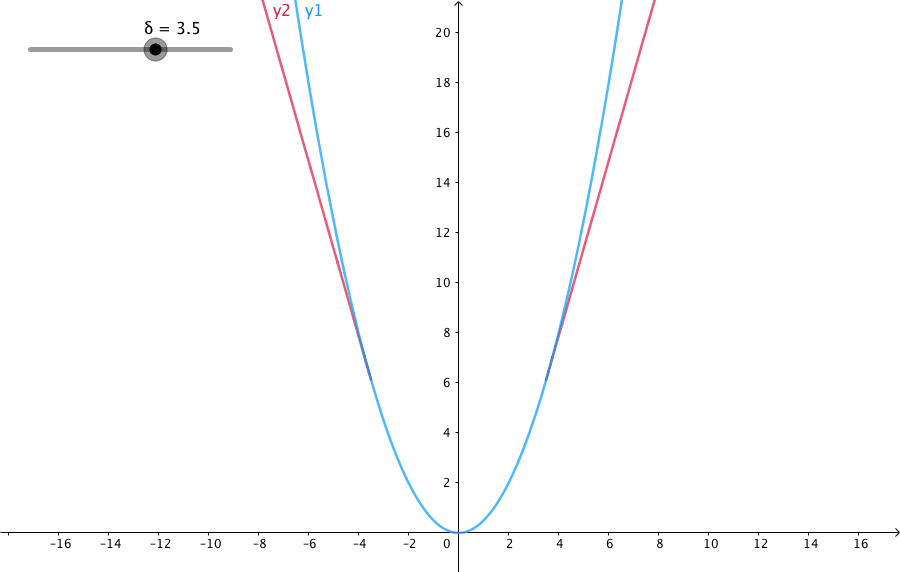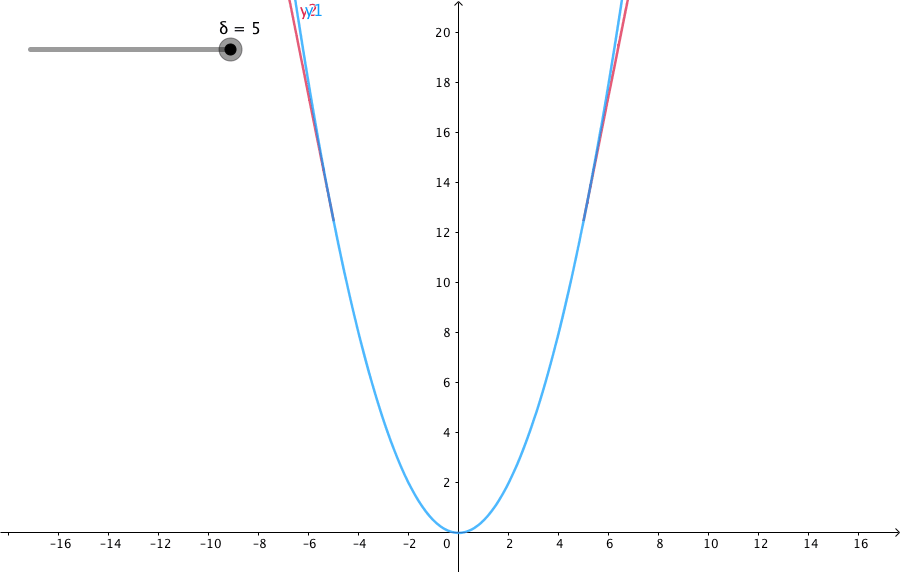
Huber损失函数
-
相比平方误差损失，Huber损失对于数据中异常值的敏感性要差一些。在值为0时，它也是可微分的。它基本上是绝对值，在误差很小时会变为平方值。误差使其平方值的大小如何取决于一个超参数δ，该参数可以调整。当δ~ 0时，Huber损失会趋向于MAE；当δ~ ∞（很大的数字），Huber损失会趋向于MSE。当预测偏差小于 δ 时，它采用平方误差,当预测偏差大于 δ 时，采用的线性误差。
-
L δ ( y , f ( x ) ) = { 1 2 ( y − f ( x ) ) 2 f o r ∣ y − f ( x ) ∣ ≤ δ δ ∣ y − f ( x ) ∣ − 1 2 δ 2 otherwise L_δ(y,f(x))=\begin{cases} \frac{1}{2}(y-f(x))^2 &for|y-f(x)|\leqδ\\ δ|y-f(x)|-\frac{1}{2}δ^2 &\text{otherwise}\\ \end{cases} Lδ(y,f(x))={21(y−f(x))2δ∣y−f(x)∣−21δ2for∣y−f(x)∣≤δotherwise
-
δ 是 HuberLoss 的参数，y是真实值，f(x)是模型的预测值, 且由定义可知 Huber Loss 处处可导。δ的选择非常关键，因为它决定了你如何看待异常值。残差大于δ，就用L1（它对很大的异常值敏感性较差）最小化，而残差小于δ，就用L2“适当地”最小化。
-
-
def huber(true, pred, delta): loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2)) return np.sum(loss) -
相比于最小二乘的线性回归，HuberLoss降低了对离群点的惩罚程度，所以 HuberLoss 是一种常用的鲁棒的回归损失函数。
-
-
Training candidates with early-stopping.
-
本文引入了一个提前停止机制来减少评估候选对象的计算开销。具体地，本文的(a)在约束迭代优化的第一次迭代之后，通过提前停止和最终精度对样本进行排序，(b)计算排序相关性，以及©找到相关性超过特定阈值(例如，0.92)的时期e，如下图所示。
-
-
等级相关性与epoch。相关阈值(青色)为0.92。
-
对于所有剩余的候选者，本文只训练e个时期的(A，h)来近似acc(A，h)。这允许使用少得多的训练迭代来评估每个查询的样本。
-
-
Training the predictor with Huber loss.
- 在获得预训练的架构嵌入之后，首先在嵌入层冻结的情况下训练预测器50个epoch。然后，以降低的学习率训练整个模型另外50个epoch。本文采用Huber损失来训练精度预测器，即 L = 0.5 ( y − y ^ ) 2 i f ∣ y − y ^ ∣ < 1 e l s e ∣ y − y ^ ∣ − 0.5 \mathcal{L}=0.5(y-\hat{y})^2 ~~~if~| y-\hat{y} |<1 ~else~|y-\hat{y}|-0.5 L=0.5(y−y^)2 if ∣y−y^∣<1 else ∣y−y^∣−0.5，其中y和 y ^ \hat{y} y^分别是预测和基本事实标签。这防止了模型被异常值所支配，异常值会混淆预测值。
Stage 3: Using predictor
- 所提出方法的第三阶段是基于自适应遗传算法的迭代过程[Adaptive probabilities of crossover and mutation in genetic algorithms]。来自第二阶段的最佳执行架构-配方对作为第一代候选的一部分被继承。
- 在每一次迭代中，本文将变异引入到候选对象中，并根据给定的约束条件生成一组子 C ⊂ Ω \mathcal{C} ⊂ Ω C⊂Ω 。使用预训练的准确度预测值u来评估每个子对象的分数，并为下一代选择前K名得分最高的候选对象。在每次迭代后计算最高分的增益，并在改进达到饱和时终止循环。最后，基于预测器的进化搜索产生高精度的神经网络结构和训练配方。
- 请注意，使用精度预测器，搜索网络以适应不同的使用场景只会产生可忽略不计的成本。这是因为准确性预测器可以在不同的资源约束下充分重用，而基于预测器的进化搜索只需要CPU分钟。
Predictor search space
- 本文的搜索空间包括训练配方和架构配置。训练配方的搜索空间以优化器类型、初始学习率、权重衰减、mixup ratio、drop out ratio、stochastic depth drop ratio以及是否使用模型指数移动平均(EMA)为特征。架构配置搜索空间基于反向残差块，包括输入分辨率、内核大小、扩展、每层通道数和深度。
- 在只有配方的实验中，只在固定的架构上调整训练配方。然而，对于联合搜索，在**上表【本文实验中的网络结构配置和搜索空间】**的搜索空间中搜索训练配方和架构。 总 的 来 说 ， 这 个 空 间 包 含 了 1 0 17 个 候 选 架 构 和 1 0 7 个 可 能 的 训 练 方 案 \color{red}{总的来说，这个空间包含了10^{17}个候选架构和10^7个可能的训练方案} 总的来说，这个空间包含了1017个候选架构和107个可能的训练方案。探索这样一个巨大的搜索空间来寻找一个最佳的网络架构及其相应的训练方法是很重要的。
Experiments
- 在本节中，首先在缩小的搜索空间中验证本文的搜索方法，以发现给定网络的训练方法。然后，评估本文的搜索方法的联合搜索架构和训练配方。本文使用PyTorch ，并在ImageNet 2012分类数据集上进行搜索。在搜索过程中，从整个数据集中随机抽取200个类来减少训练时间。然后，从200类训练集中随机保留10K图像作为验证集。
Recipe-only search
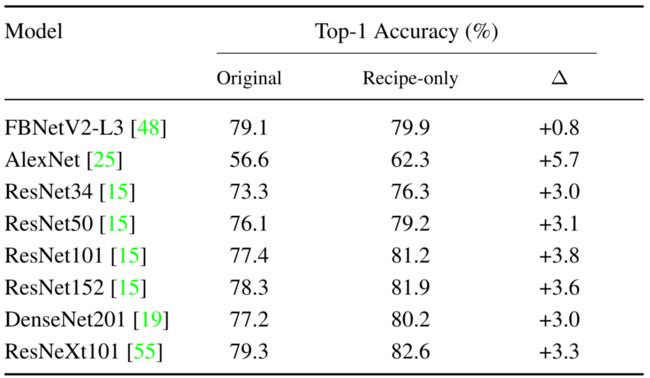
- 为了证明即使是现代NAS产生的体系结构的性能也可以通过更好的训练方案来进一步提高，本文针对固定体系结构优化了训练方案。本文采用FBNetV2-L3 作为本文的基础架构，这是一种DNAS搜索架构，使用[FBNet-V2]中使用的原始训练方法实现了79.1%的top-1准确性。
- 本文在约束迭代优化中设置样本池大小n = 20K，批量m = 48，迭代T = 4。本文在搜索期间以每个epoch 0.963的学习率衰减因子训练150个epoch的采样候选，并以3倍较慢的学习率衰减(即，每个epoch 0.9875)训练最终模型。
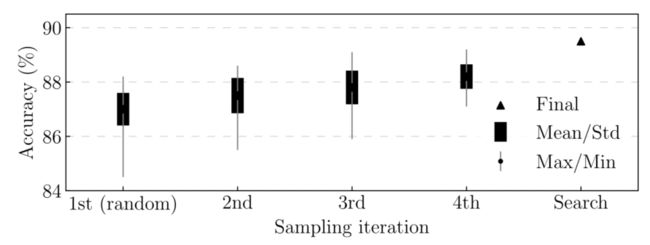
- 本文在下图中显示了每一轮的样本分布以及本文的实验中的最终搜索结果，其中第一轮样本是随机生成的。搜索到的训练配方(附录A.3)将本文的基础架构的准确性提高了0.8%。
-
-
取样和搜索过程的图示。
-
- 本文将NARS搜索的训练方法扩展到其他常用的神经网络，以进一步验证其通用性。尽管NARS搜索的训练方法是为FBNetV2-L3定制的，但它的泛化能力惊人地好，如下表所示。
-
-
在现有神经网络上搜索训练配方的准确性改进。以上，ResNeXt101指的是32x8d的变种。
-
- 在ImageNet上，NARS搜索的训练配方导致了高达5.7%的准确度增益。事实上，ResNet50比基准ResNet152高出0.9%。ResNeXt101-32x8d甚至超越了弱监督学习模型，该模型使用10亿幅弱标记图像进行训练，达到了82.2%的top-1准确率。值得注意的是，有可能通过为每个神经网络搜索特定的训练方案来实现甚至更好的性能，这将增加搜索成本。
Neural Architecture-Recipe Search (NARS)
- 搜索设置，本文执行架构和训练方案的联合搜索，以发现紧凑的神经网络。请注意，根据本文在上文的观察。缩小搜索空间，始终使用 E M A \textcolor{red}{EMA} EMA。大多数设置与仅配方搜索相同，但本文增加了优化迭代T = 5，并将样本池的FLOPs约束从400M设置为800M。本文使用包含20K个样本的样本池的80%来预训练架构嵌入层，并在上图【Stage 1: Predictor pretraining】中绘制剩余20%的验证。
- 在基于预测器的进化搜索中，本文设置了四个不同的FLOPs约束:450M、550M、650M和750M，并发现了具有相同精度预测器的四个模型(即FBNetV3-B/C/D/E)。本文进一步缩小和放大最小和最大模型，并生成FBNetV3-A和FBNetV3F/G，以分别适应更多的使用场景，使用[efficientnet]中提出的复合缩放。
- **训练设置,**对于模型训练，本文使用基于两步蒸馏的训练过程:
- (1)首先用具有基本事实标签的搜索配方训练最大的模型(即FBNetV3-G)。
- (2)然后，用蒸馏法训练所有的模型(包括FBNetV3-G本身)，这是[Once for all: Train one network and specialize it for efficient deployment，Bignas: Scaling up neural architecture search with big single-stage models]中采用的典型训练技术。
- 与[once for all,Bignas]中的就地蒸馏法不同，这里的教师模型是从步骤(1)中导出的ImageNet预训练FBNetV3-G。训练损失是两个分量的和： 按 0.8 缩 放 的 蒸 馏 损 失 和 按 0.2 缩 放 的 交 叉 熵 损 失 \textcolor{blue}{按0.8缩放的蒸馏损失和按0.2缩放的交叉熵损失} 按0.8缩放的蒸馏损失和按0.2缩放的交叉熵损失。在训练过程中，在8个节点和每个节点8个GPU的分布式训练中使用同步批处理规范化。在5个epoch的预热后，用每个epoch 0.9875的学习率衰减因子训练400个epoch的模型。
- 本文分别用搜索到的FBNetV3-B和FBNetV3-E的训练配方来训练比例模型FBNetV3-A和FBNetV3-F/G，仅将FBNetV3-F/G的随机深度下降比增加到0.2。更多训练详情请参见附录A.5。
- 搜索到的模型：本文将搜索到的模型与上图【ImageNet accuracy vs. model FLOPs comparison of FBNetV3 with other efficient convolutional neural networks.】中的其他相关NAS基准和手工制作的紧凑神经网络进行了比较，并在下表中列出了详细的性能指标比较，在下表中，本文根据模型的最高准确性对模型进行了分组。
-
-
不同紧凑神经网络的比较。对于基线，本文引用原始论文中ImageNet上的统计数据。本文的结果是加粗的。*:群体参数化。请参见A.6，了解有关训练技巧和其他效率网对比的讨论。
-
- 在所有现有的高效模型中，如EfficientNet、MobileNetV3 、ResNeSt 和FBNetV2 ，本文搜索的模型在精度-效率权衡方面提供了实质性的改进。
- 例如，在低计算成本制度下，FBNetV3-A仅使用357M FLOPs就实现了79.1%的顶级精度(比使用类似FLOPs的MobileNetV3-1.25x 高2.5%)。在高精度领域，FBNetV3-E的精度比ResNeSt-50 高0.2倍，而FBNetV3-G的精度与EfficientNetB4 相当，但FLOPs比ResNeSt-50少7倍。请注意，本文通过使用更大的教师模型进行蒸馏，进一步提高了FBNetV3的准确性，如附录A.7所示。
Transferability of the searched models
- CIFAR-10上的分类：本文进一步扩展了在CIFAR-10数据集上搜索的FBNetV3，该数据集具有来自10个类别的60K个图像，以验证其可转移性。请注意，与[efficientnet]将基本输入分辨率放大到224×224不同，本文将原始基本输入分辨率保持为32×32，并根据缩放比例放大更大模型的输入分辨率。
- 本文还将第二个二步模块替换为一步模块，以适应低分辨率输入。为了简单起见，不包括蒸馏。在下图中比较了不同模型的性能。同样，本文搜索的模型明显优于效率净基线。
-
-
CIFAR-10数据集上的精度与FLOPs比较。
-
- COCO上的检测：为了进一步验证所搜索的模型在不同任务上的可移植性，本文使用FB-NetV3作为主干特征提取器的替代，用于具有conv4 (C4)主干的faster R-CNN，并在COCO检测数据集上与其他模型进行比较。本文采用[Detectron2.](https://github. com/facebookresearch/detectron2)中的大多数训练设置，具有3倍的训练迭代，同时使用同步批量归一化，将学习率初始化为0.16，打开EMA，将非最大抑制(NMS)减少到75，并在预热后将学习率计划更改为余弦。请注意，本文只迁移搜索到的架构，并对所有模型使用相同的训练协议。
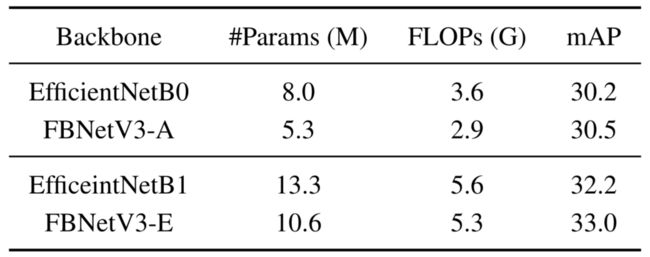
- 本文在下表中显示了详细的COCO检测结果。与EfficientNet backbones相比，在类似或更高的mAP下，本文的FBNetV3将FLOPs和参数数量分别减少了18.3%和34.1%。
-
-
COCO上不同主干的faster RCNN的目标检测结果。
-
Ablation study and discussions
- 在本节中，将重温联合搜索带来的性能提升、基于预测器的进化搜索的重要性，以及几种训练技术的影响和通用性。
Architecture and training recipe pairing.
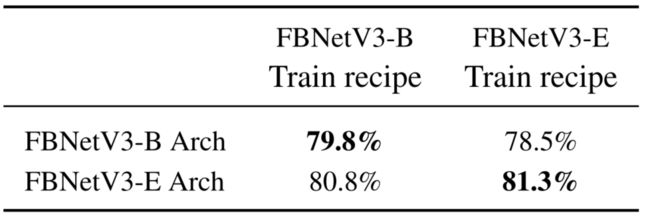
- 本文的方法为不同的模型产生不同的训练配方。例如，本文观察到较小的模型倾向于偏好较小的正则化(例如，较小的随机深度下降比和混合比)。为了说明神经架构配方搜索的重要性，本文交换了为FBNetV3-B和FBNetV3-E搜索的训练配方，观察到这两种模型的精确度都有显著下降，如下表所示。这突出了正确的体系结构方案配对的重要性，强调了传统NAS的衰落:忽略训练方案而只搜索网络体系结构无法获得最佳性能。
-
-
具有交换训练配方的搜索模型的精度比较。
-
Predictor-based evolutionary search improvements.
- 基于预测器的进化搜索在约束迭代优化的基础上产生了实质性的改进。为了证明这一点，本文比较了在相同FLOPs约束条件下从第二搜索阶段获得的最佳性能候选与最终搜索的FBNetV3(见下表)。观察到，如果丢弃第三级，精度会下降高达0.8%。因此，第三个搜索阶段虽然只需要很少的成本(即几分钟的CPU时间)，但对最终模型的性能同样至关重要。
-
-
基于预测的进化搜索的性能改进。*:从约束迭代优化中导出的模型。
-
Impact of distillation and model averaging
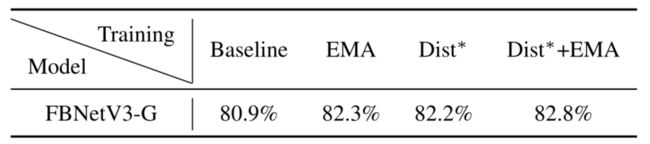
- 本文在下表中显示了不同训练配置下FBNetV3-G上的模型性能，其中基线指的是没有EMA或蒸馏的普通训练。EMA带来了更高的准确性，尤其是在训练的中间阶段。本文假设EMA本质上是一个强大的“集合”机制，从而提高单一模型的准确性。本文还观察到蒸馏带来了显著的性能改进。这与[once for all，Bignas]中的观察结果一致。注意由于老师模型是预训的FBNetV3-G，所以FBNetV3-G是自提的。EMA和蒸馏的结合将模型的前1名准确率从80.9%提高到82.8%。
-
-
使用EMA和蒸馏提高性能。*:蒸馏训练
-
Conclusion
- 顾名思义，以前的神经结构搜索方法只搜索结构，使用一组固定的训练超参数(即“训练方法”)。因此，以前的方法忽略了更高精度的架构副本组合。然而，本文的NARS没有，它是第一个同时在架构和训练方法上联合搜索像ImageNet这样的大型数据集的算法。至关重要的是，NARS的预测器对“free”架构统计数据(即FLOPs和#参数)进行预训练，以显著提高预测器的采样效率。在训练和使用预测器之后，得到的FBNetV3体系结构-配方对在ImageNet分类上达到了最先进的每FLOP精度。
A. Appendix
A.1. Training recipe used in Table 1
- 配方1和配方2共享相同的批量256、初始学习速率0.1、重量衰减为4×105、SGD优化器和余弦学习速率表。配方1训练模型30个epoch，配方2训练模型90个epoch。本文不会在Recipe-1或Recipe-2中引入训练技术，如dropout、随机深度和mixup。
- 当训练配方-1和配方-2使用相同的#epoch但不同的权重衰减时，得到了相同的观察结果:当权重衰减分别为 1 e − 4 1e^{-4} 1e−4和 1 e − 5 1e^{-5} 1e−5时，ResNet18 (1.4x宽度)的准确度比ResNet18 (2x深度)高0.25%和低0.36%。
A.2. Base architecture in recipe-only search
- 本文在下表中显示了仅用于配方搜索的基础架构(FBNetV2-L2的缩放版本)，输入分辨率为256×256。
-
-
仅配方搜索中使用的基线架构。模块符号与表【The network architecture configuration and search space in our experiments.】相同。如果输入和输出通道相等，跳过块指的是相同的连接，否则是1×1 conv。
-
- 这是在上文中的训练配方搜索中使用的基础架构。它在ImageNet上实现了79.1%的顶级准确率，并使用了FBNetV2的原始训练方法。使用搜索到的训练配方，它达到了79.9%的ImageNet top-1准确率。
A.3. Search settings and details
-
在仅配方搜索实验中，本文将early-stop等级相关阈值设置为0.92，并且发现对应的early-stop时期为103。在基于预测器的进化搜索中，本文将初始代的群体设置为100(来自约束迭代优化的50个最佳执行候选和50个随机生成的样本)。
-
从每个候选对象中产生24个子对象，并为下一代挑选前40名候选对象。大部分的设置都是由建筑和训练配方的联合搜索共享的，除了提早停止的纪元是108。准确度预测器由一个嵌入层(架构编码器层)和一个额外的隐藏层组成。对于联合搜索，嵌入宽度是24(注意，对于仅配方搜索，没有预训练的嵌入层)。对于联合搜索，本文将最小和最大FLOPs约束分别设置为400M和800M。
-
在约束迭代优化中选择m个性能最佳的样本包括两个步骤:
- (1)将FLOP范围平均分成m个仓，
- (2)在每个仓内挑选具有最高预测得分的样本。
-
本文在下表中显示了详细的搜索训练配方。也发布搜索到的模型。
-
-
Searched training recipe.
-
A.4. Comparison between recipe-only search and hyperparameter optimizers
- 许多著名的超参数优化器(ASHA、Hyberband、PBT)都在CIFAR10上进行评估。一个例外是[Using a thousand optimization tasks to learn hyperparameter search strategies]，它通过搜索优化器、学习率、权重衰减和动量，报告了ImageNet上ResNet50的0.5%的增益。相比之下，在相同空间(不含EMA)下的食谱搜索将ResNet50的准确率提高了1.9%，从76.1%提高到78.0%。
A.5. Training settings and details
-
对于最终的模型，本文使用具有8个节点的分布式训练，并且通过分布式节点的数量来按比例增加学习速率(例如，对于8节点训练是8倍)。每个节点的批处理大小设置为256。本文在训练中使用标签平滑和自动增强。此外，本文将批量标准化参数的重量衰减和动量分别设置为零和0.9。
-
本文将EMA模型实现为原始网络的副本(它们在t = 0时共享相同的权重)。在每次反向传递和模型权重更新后，本文将EMA权重更新为：
-
w t + 1 e m a = α w t e m a + ( 1 − α ) w t + 1 , ( 2 ) w_{t+1}^{ema}=αw_t^{ema}+(1-α)w_{t+1},(2) wt+1ema=αwtema+(1−α)wt+1,(2)
-
其中 w t + 1 e m a w^{ema}_{t+1} wt+1ema、 w t e m a w^{ema}_t wtema和 w t + 1 w_{t+1} wt+1是指步骤t+1的EMA权重、步骤t的EMA权重和t+1的模型权重。本文在ImageNet、CIFAR-10和COCO上的实验中分别使用了0.99985、0.999和0.9998的EMA衰减α。本文在下图中进一步提供了FBNetV3-G的训练曲线。
-
-
Training curve of the search recipe on FBNetV3-G.
-
-
基线模型(例如AlexNet、ResNet、DenseNet和ResNeXt)采用PyTorch开源实现，没有任何架构变化。输入分辨率为224×224。
A.6. More discussions on training tricks
-
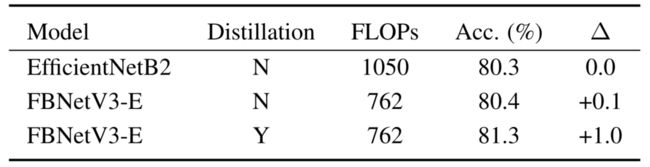
本文了解到EfficientNet不使用蒸馏。为了公平比较，本文报告了未经蒸馏的FBNetV3精度。本文在下表中提供了一个例子:与EfficientNet相比，在没有蒸馏的情况下，FBNetV3实现了更高的精度，同时FLOPs减少了27%。然而，本文所有的训练技巧(包括EMA和蒸馏)都在其他基线中使用，包括BigNAS和OnceForAll。
-
-
带蒸馏和不带蒸馏的模型比较。
-
-
Generality of stochastic weight averaging via EMA.
-
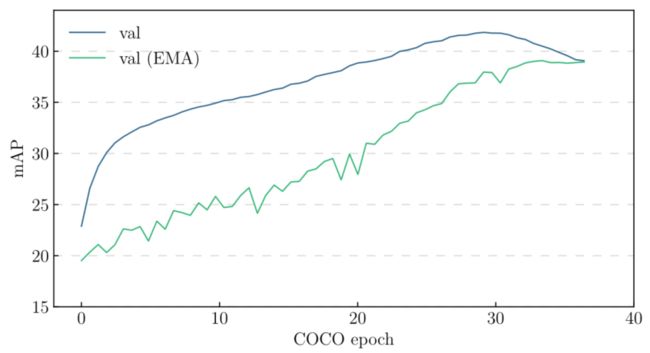
本文观察到，通过EMA进行随机加权平均可以显著提高分类任务的准确性，如之前所述[Large scale gan training for high fidelity natural image synthesis，Momentum contrast for unsupervised visual representation learning]。本文假设这种机制可以作为一种通用技术来改进其他DNN模型。为了验证这一点，本文使用ResNet50和ResNet101主干，在COCO对象检测上训练RetinaNet。本文遵循大多数默认的训练设置，但引入了EMA和余弦学习率。本文观察到与分类任务相似的训练曲线和行为，如下图所示：
-
-
具有ResNet101主干的RetinaNet在COCO对象检测上的训练曲线。
-
生成的具有ResNet50和ResNet101主链的RetinaNets 分别达到40.3和41.9的mAP，两者都大大优于[Detectron2]中报道的最佳值(ResNet50和ResNet101分别为38.7和40.4)。一个有希望的未来方向是研究这样的技术，并将其扩展到其他DNNs和应用。
-
A.7. Further improvements on FBNetV3
- 本文证明了使用具有更高精度的教师模型会进一步提高FBNetV3的精度。本文使用RegNetY -32G FLOPs(前1名准确率84.5%)作为教师模型，并提取所有FBNetV3模型。
- 本文在下图中显示了所有衍生模型，本文观察到所有模型的精度增益一致，为0.2% - 0.5%。
- ImageNet精度与模型FLOPs fbnet-v3(从giant RegNet-Y模型中提取)与其他高效卷积神经网络的比较。