《深入浅出强化学习原理入门》学习笔记（七）DQN

DQN采用的是Qleaning的基本框架，对Qlearning的修改主要体现在以下三个方面。
（1）DQN利用 深度卷积神经网络逼近值函数。
（2）DQN利用了 经验回放训练强化学习的学习过程。
（3）DQN采用 设置独立目标网络的方法来单独处理时间差分算法中的TD偏差。

本篇按照Qleaning框架、值函数逼近方法、卷积神经网络、经验回放、设置独立目标网络的顺序依次介绍。

其中，DQN的提出最大的贡献是，把认知科学的成果应用到了深度神经网络的训练之中，即经验回放和设置独立目标网络。

1、Qleaning框架

Qleaning框架中最重要的两个概念是异策略和时间差分。
异策略是指，行动策略（产生数据的策略）采用ε-greedy策略，目标策略（评估和改进策略）采用贪婪策略（每个状态取值函数最大的动作）。
时间差分方法是指，利用时间差分目标更新当前行为值函数。Qleaning的时间差分目标为

2、值函数逼近

之前介绍了很多强化学习方法，对于模型已知的系统基于动态规划的方法，对于模型未知的系统基于蒙特卡罗的方法或时间差分的方法。

这些方法的基本步骤都是评估值函数，再利用值函数改善当前的策略。都有一个基本前提，状态空间和动作空间是离散的，值函数其实是状态和行为值得表格，值函数的更新本质为表的迭代更新。所以之前讲过的强化学习算法又称表格型强化学习。

如果状态空间维数很大或者为连续空间，需要采用值函数逼近的办法表示值函数，并利用策略迭代和值迭代构建强化学习算法。

值函数逼近分为参数化逼近和非参数化逼近，其中参数化逼近又可以分为线性参数化逼近和非线性参数化逼近。

详细介绍一下参数化逼近。

当逼近的值函数结构确定时（如线性逼近时选定了基函数，非线性逼近时选定了神经网络的结构），那么值函数的逼近就等价于参数的逼近。 值函数的更新也就等价于参数的更新。需要利用试验数据来更新参数值。

从6.1-6.3的更新过程可以看出，值函数更新的过程就是向着目标函数的逼近。对于表格型强化学习，更新值函数，只有当前St处的值函数该表，其他地方的值函数不变。采用值函数逼近方法改变值函数时，因为更新的是参数，任意状态处的值函数都会改变。

值函数的更新可分为增量式学习方法和批学习方法。

增量式学习：随机梯度下降法

基于梯度的蒙特卡罗值函数评估

增量式学习：半梯度算法

要更新的参数不仅出现在要估计的值函数中，还出现在目标值函数中，但是只考虑对估计值函数的影响，忽略对目标值函数的影响，这种方法称为不完全的梯度法（半梯度算法）。
基于半梯度的TD值函数评估

基于半梯度的Sarsa算法

线性逼近

线性逼近的好处是只有一个最优值，所以可以收敛到全局最优，φ（s）为状态s处的特征函数（基函数）。

把线性逼近值函数代入随机梯度下降和半梯度下降，可以得到参数的更新公式。

批学习方法

特点：计算复杂，但是计算效率高。

非线性化逼近：神经网络

前向网络

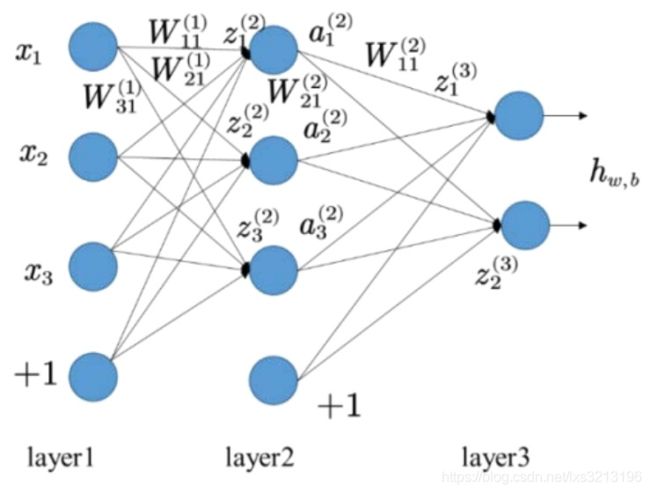
上图为前向神经网络，网络包括三层，用nl=3表示。将第l层记为Ll，第一层为输入层L1，第二层为隐含层，第三层为输出层L3。神经网络的参数用（W,b）表示W是第l层第j单元和第l+1层第i单元的连接参数,b是第第l+1层第i单元的偏置项。z表示第l层第i个单元的输入加权和，a表示第l层第i个单元激活，a=f(z)。

本例神经网络的前向计算可以总结如下

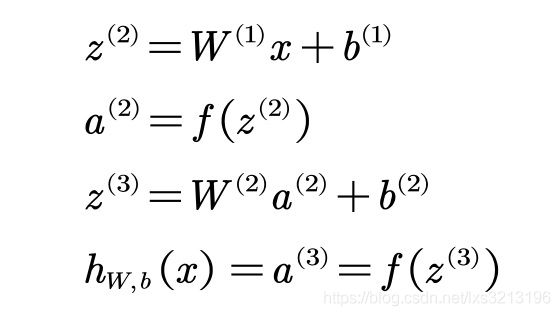
前向网络的反向求导

训练样本
单个样本的平方损失函数

训练集T上的损失函数，第一项为均方损失，目的是让神经网络逼近训练数据；第二项是权值正则项，目的是防止网络过拟合。

利用梯度下降法来更新每个权值的W和b

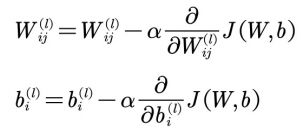
将损失函数代入得到损失函数对权值的梯度。


前向神经网络残差反向传播

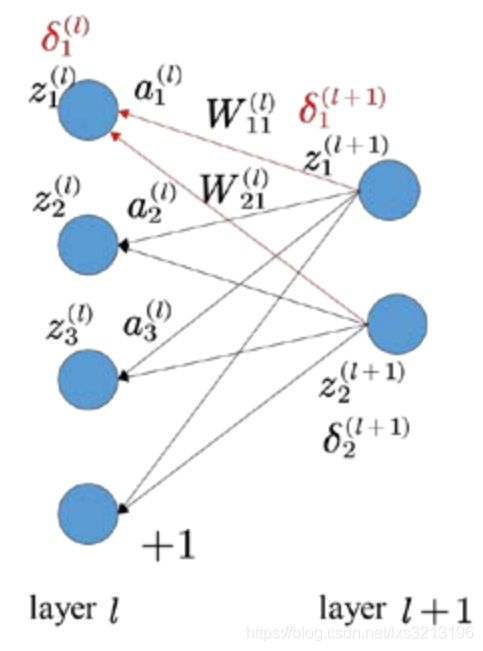
神经网络的每层都可以看做基于上一层的新的基函数，后面一层是前面一层的抽象，这样可以对高度输入降维。和浅层网相比，深度网络具有更强的表示能⼒。随着深度网络技术的突破性发展，深度学习已在各行各业广泛应用，尤其是卷积神经网络（CNN），被⼴泛应用于强化学习中，是深度强化学习算法最常用的深度网络。

3、卷积神经网络

在深度神经网络中，网络的参数个数往往达到几万甚至几百万，很难训练。卷积神经网络则通过卷积和池化降低参数个数，加快网络加速训练过程。

卷积运算

也写作s(t)=(x*w)t，第一个参数x通常为输入，第二个参数w为核函数，输出称为特征映射。在深度学习中，输入往往是多维数组，如输入是图片时，可表示为二维数组。

下图为一个二维卷积过程实例。

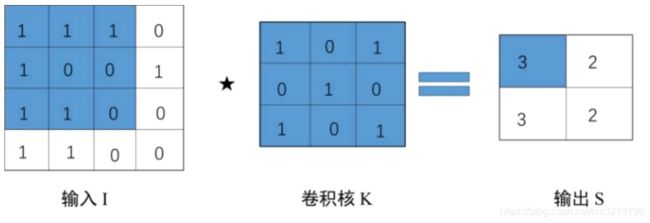
卷积神经网络将卷积操作引入神经网络的设计中，其中卷积核对应权重向量，卷积操作通过系数连接和权值共享帮助改进神经网络系统。

在前向神经网络中，每层神经元之间的连接是全连接，卷积核使相邻层的连接不再是全连接，而是使神经元只和临近的神经元连接。

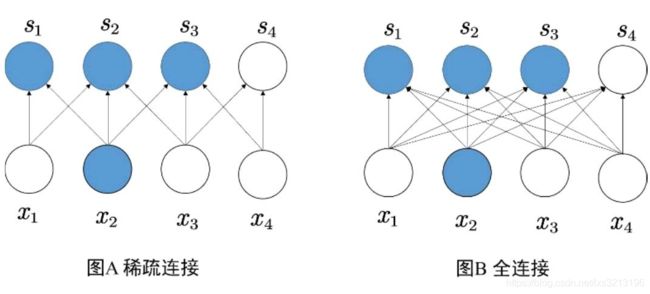
在稀疏连接中，下一层的元素只通过和与上一层部分输入相连，相连的输入个数由卷积核的大小决定，卷积核相当于神经元中的感受野。稀疏连接大大减少了深度神经网络的权值。

权值共享，是指神经元在连接下一层神经元时使用相同的权值。

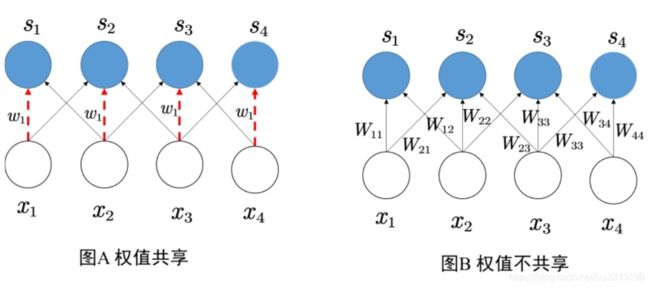
在权值共享机制中，权值处处相同，再次急剧减少了神经网络中的权值数。

池化

池化，就是用某区域的统计特征来表示该区域。

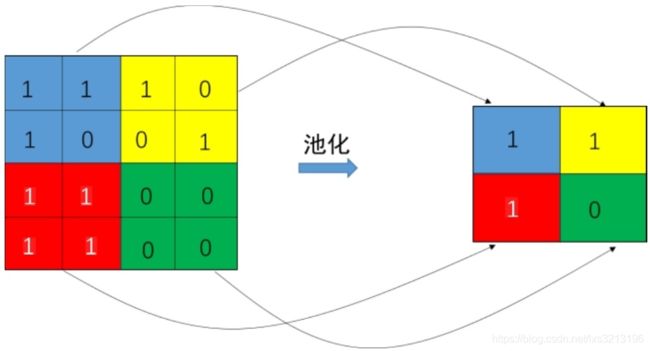
池化操作可以参数化，比如区域内所有元素相加再乘以一个可训练的参数再加上一个可训练的偏置参数。

典型卷积神经网络LeNet

在卷积神经网络（CNN）中，卷积和池化常常交替使用。下图为典型的卷积神经网络LeNet网络结构。

（1）输入层。输入一张32*32像素大小的图像。

（2）卷积层1即C1层。用5×5的卷积核对输⼊为32×32的图像做卷积操作，特征图的大小变为28××28。从输入层到C1层一共用了6个不同的卷积核，每个卷积核得到一幅特征图，所以C1层一共有6个特征图。每个卷积核可训练参数为25个，每个卷积有一个偏置，所以C1共有（5*5+1）*6=156个可训练参数。

（3）池化层1，即下采样S2层。这里采用的池化操作为参数化池化操作，把池化区域内所有元素相加再乘以一个可训练的参数，然后加上一个可训练的偏置参数。每个特征图对应一组可训练的池化参数，6个特征图共有12个可训练的参数。
公式如下，其中


为可训练参数，f为激活函数。

（4）卷积层2，即C2层。

从S2到C1，池化层的6个特征图经过与卷积核Kij卷积操作，得到C3层的16个特征图。一共有60个不同的卷积核，每个卷积有55=25个可训练参数，C3层每个特征图都有一个偏置值，所以C3层可训练参数为5560+116=1516个。

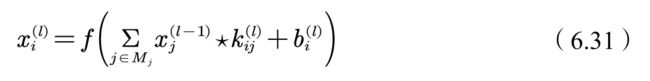
（5）池化层2即S4。由16个55的特征图构成。一共可训练参数为162=32个。

（6）卷积层3即C5层，有120个特征图，不同卷积核个数为16*120，因此该层可训练的 参数个数为16×120×5×5+120=48120。

（7）全连接层，F6层，共84个单元，与C5全连接。⼀共可训练的参数个数为84× 120+84=10164。

（8）输出层共10个单元，每个单元84个输入，每个单元的输出由欧式径向基函数给出。具体计算公式为

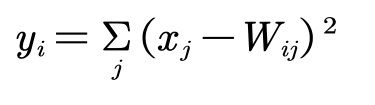
其中x为F6层的输出，y为输出。

卷积神经网络的反向传播

（1）卷积核梯度的求解

和前向神经网络的反向梯度计算过程⼀样，卷积神经网络也需要先计算当前层的残差

有了残差之后，损失函数关于卷积核的导数可以写成
（2）池化层梯度的求解

当前层的⽹络残差为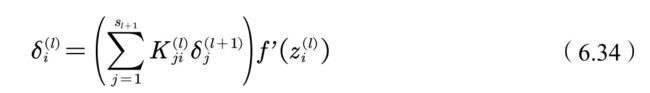
在池化层中，梯度反向传播时需要经过下采样，因此定义下采样为
得到池化层梯度反向传播公式为

4、DQN：利用经验回放训练学习过程

我们睡觉的时候，海马体会把⼀天的记忆重放给⼤脑皮层。利⽤这个启发机制，DeepMind团队的研究⼈员构造了⼀种神经⽹络的训练方法：经验回放。

训练神经网络时，存在的假设是训练数据是独立同分布的， 但是通过强化学习采集的数据之间存在着关联性，利⽤这些数据进⾏顺序 训练，神经网络不稳定。经验回放可以打破数据间的关联，训练收敛且稳定。

在强化学习过程中，智能体将数据存储到⼀个数据库中，再利用均匀随机采样的方法从数据库中抽取数据，然后利用抽取的数据训练神经网络。

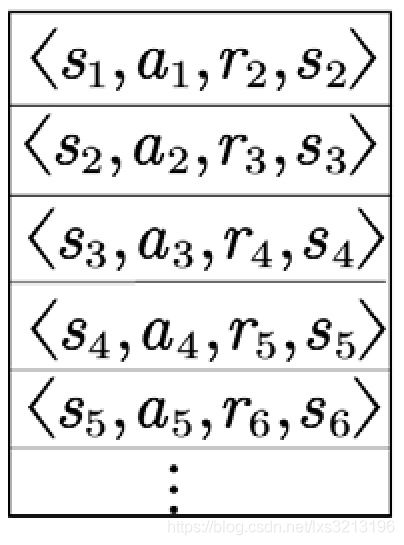
5、DQN:设置目标网络处理时间差分算法中的TD偏差

与表格型的Qlearning算法不同的是，利⽤神经⽹络对值函数进行逼近时，值函数的更新步更新的是参数 ，更新方法是梯度下降法。


上式为TD目标

我们称计算TD目标时所用的网络为TD网络。在DQN算法出现之前， 利⽤神经网络逼近值函数时，计算 TD 目标的动作值函数所⽤的⽹络参数，与梯度计算中要逼近的值函数所⽤的⽹络参数相同，这样就容易导致 数据间存在关联性，从而使训练不稳定。

为了解决此问题，DeepMind提出计算TD目标的网络表示为；计算值函数逼近的网络表示为；用于动作值函 数逼近的网络每⼀步都更新，用于计算 TD目标的网络则是每个固定的 步数更新⼀次。

所以值函数更新变为下式

6、DQN伪代码