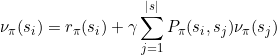LET IT BE

《深入浅出强化学习：原理入门》学习笔记

1 绪论

1.1强化学习可以解决什么问题

用一句话来概括强化学习能解决的问题就是：智能决策问题。更确切地说是序贯决策问题。

序贯决策问题：需要连续不断地做出决策，才能实现最终目标的问题

1.2 强化学习如何解决问题

监督学习解决的问题：智能感知的问题。监督学习需要感知到当前的输入是怎样，并给出对应的输出（标签）。智能感知必不可少的前提是大量长相差异化的输入以及与输入相关的标签。

监督学习解决问题的方法：输入大量带有标签的数据，让智能体从中学到输入的抽象特征并预测。

强化学习解决的问题：序贯决策问题。不关心输入长什么样，只关心当前输入下应该采用什么动作才能实现最终的目标。简单地说就是，当前采用什么动作可以使得整个任务序列达到最优。

强化学习解决问题的方法：智能体不断地与环境进行交互，不断尝试，通过动作与环境进行交互时，环境会返回给智能体一个当前的回报，智能体则根据当前的回报评估所采取的动作：有利于实现目标的动作被保留，不利于实现目标的动作被衰减。

总的来说，强化学习和监督学习都需要大量的数据进行训练，前者需要带有回报的交互数据，后者需要的则是标签数据。

1.3 强化学习的算法分类

根据强化学习算法是否依赖模型分：基于模型的强化学习算法和无模型的强化学习算法。有模型算法先利用与环境交互得到的数据学习系统或者环境模型，再基于模型进行序贯决策。无模型算法直接利用与环境交互得到的数据改善自身的行为。
根据策略的更新和学习方法分：基于值函数的强化学习算法、基于直接策略搜索的强化学习计算法和AC的方法。
根据环境返回的回报函数是否已知分：正向强化学习和逆向强化学习。

从广义上将，强化学习是序贯决策问题。序贯决策问题既包含马尔科夫过程的决策，也包含非马尔科夫决策过程的决策。可以将强化学习纳入到马尔科夫决策过程MDP的框架之内。再根据转移概率P是否已知，可以分为基于模型的动态规划方法和基于无模型的强化学习方法。这两个类别都包括策略迭代算法、值迭代算法和策略搜索算法。另外，在无模型的强化学习方法中，每类算法又分为online和offline两种。

1.4 强化学习的发展历史及趋势

第一个关键点：1998年，Richard S. Sutton出版了Reinforcement Learning：An introduction

总结了1998年以前的各种强化学习算法的发展。

第二个关键点：2013年DeepMind提出DQN(Deep Q Network)，将深度网络与强化学习算法结合形成深度强化学习（Deep Reinforcement Learning，DRL）。

发展趋势：与深度学习结合、理论分析更强、算法更稳定高效、与脑科学联系紧密

2 马尔科夫决策过程

2.1 马尔科夫决策过程理论讲解

第一个概念：马尔科夫性

系统的下一个状态仅与当前的状态有关，而与以前的状态无关。即：若状态 $\small S_{t}$ 是马尔科夫的，则：

$\small P(S_{t+1}|S_{t}) = P(S_{t+1}|S_{1},\cdot \cdot \cdot ,S_{t})$

第二个概念：马尔科夫过程

马尔科夫过程：一个二元组（S,P），且满足：S是有限状态集合，P是状态转移概率矩阵

第三个概念：马尔科夫决策过程

马尔科夫决策过程：一个五元组 $\small (S,A,P,R,\gamma )$ ，其中S是有限状态集合，A是有限动作集合，P是状态转移概率矩阵，R是回报函数， $\small \gamma$ 是折扣因子，用来计算累计回报。

马尔科夫决策过程的状态转移概率（动态特性）：

$\small P^a_{ss'}=P[S_{t+1}=s'|S_{t}=s,A_{t}=a]$

有些情况下，也可以写成：

$\small P^a_{ss'}=P[S_{t+1}=s',R_{t+1}=r|S_{t}=s,A_{t}=a]$

这是因为考虑到了即时回报函数也有可能是一个随机变量。

强化学习的目标是给定一个马尔科夫决策过程，寻找最优策略。

所谓策略是指状态到动作的映射，策略常用符号 $\small \pi$ 表示，它是指给定状态s时，动作集上的一个分布：

$\small \small \pi(a|s)=p[A_{t}=a|S_{t}=s]$

其含义是策略 $\small \pi$ 在每个状态s指定一个动作概率。

要注意，策略也可以是确定性的，即在某一种状态下采取的动作时确定的。

所谓最优策略是指得到的累计回报最大，累计回报的定义如下：

$\small G_{t}=R_{t+1}+\gamma R_{t+2}+\cdot \cdot \cdot =\sum_{k=0}^{ \infty }\gamma^k R_{t+k+1}$

为了使用一个确定量来描述状态 $\small s_{1}$ 的价值，可以考虑使用累计回报 $\small G_{1}$ 来衡量，但其是一个随机变量，因此考虑其期望值，并作为状态值函数的定义。

（1）状态-值函数和状态-行为值函数

当智能体采用策略π时，累计回报服从一个分布，累计回报在状态s处的期望值定义为状态-值函数：

$\small \small \nu _{\pi}(s)=E_{\pi}[\sum_{k=0}^{ \infty }\gamma^k R_{t+k+1}|S_{t}=s]$

相应地，状态-行为值函数为：

$\small q _{\pi}(s,a)=E_{\pi}[\sum_{k=0}^{ \infty }\gamma^k R_{t+k+1}|S_{t}=s,A_{t}=a]$

（2）状态-值函数和状态-行为值函数的贝尔曼方程

$\small \nu(s)=E[G_{t}|S_{t}=s]=E[R_{t+1}+\gamma\nu(S_{t+1})|S_{t}=s]$

$\small q_{\pi}(s,a)=E[R_{t+1}+\gamma q(S_{t+1},A_{t+1})|S_{t}=s,A_{t}=a]$

对状态-值函数进行分解，得到：

$\small \nu_{\pi}(s)=\sum_{a \in A}\pi(a|s)q_{\pi}(s,a)$

$\small q_{\pi}(s,a)=R_{s}^a+\gamma\sum_{s'\in S}P_{ss'}^a\nu_{\pi}(s')$

即根据策略在状态s的条件下采取动作a得到的累计回报q(a,s）是当前的累计回报 $\small R_{s}^a$ 加上未来各种可能的状态得到的回报的加权平均。整合两个公式可以得到：

$\small \small q_{\pi}(s,a)=R_{s}^a+\gamma\sum_{s'\in S}P_{ss'}^a\sum_{a'\in A}\pi(a'|s')q_{\pi}(s',a')$

（3）最优状态值函数和最优状态状态-行为值函数的贝尔曼最优方程：

$\small \nu^*(s)=\max_{a}R_{s}^a+\gamma\sum_{s' \in S}P_{ss'}^a\nu^*(s)$

$\small q^*(s,a)=R_{s}^a+\gamma\sum_{s' \in S}P_{ss'}^a\max_{a'}q^*(s',a')$

2.2 强化学习算法的形式化描述

定义一个离散时间有限范围的折扣马尔科夫决策过程 $\small M=(S,A,P,r,\rho _{0},\gamma,T)$ ,其中S为状态集，A为动作集， $\small P:S\times A\times S\rightarrow R$ 是转移概率， $\small r:S\times\rightarrow A[-R_{max},R_{max}]$ 为立即回报函数， $\small \rho_{0} :S\times A\rightarrow R$ 是初始状态分布， $\small \gamma\sqsupset \in [0,1]$ 为折扣因子，T为水平范围（其实就是步数）。 $\small \tau$ 为一个轨迹序列，即 $\small \tau=(s_{0},a_{0},s_{1},a_{1},\cdot \cdot \cdot )$ ，累计回报为 $\small R=\sum_{t=0}^{T}\gamma ^tr_{t}$ ,强化学习的目标是找到最优策略 $\small \pi$ ,使得该策略下的累计回报期望最大，即 $\small max\int R(\tau)p_{\pi}(\tau)d\tau$

3 基于模型的动态规划方法

基于模型的强化学习可以利用动态规划的思想来解决。利用动态规划可以解决的问题需要满足两个条件：一是整个优化问题可以分解为多个子优化问题；二是子优化问题的解可以被存储和重复利用。

由于强化学习可以归于马尔科夫决策问题的框架之下，通过上一节得到的状态-值函数贝尔曼最优方程可以看出，马尔科夫决策问题符合使用动态规划的两个条件，因此可以使用动态规划来解决基于模型的强化学习问题。

3.1 策略迭代算法

策略迭代算法包括策略评估和策略改进两个步骤。在策略评估中，给定策略，通过数值迭代算法不断计算该策略下每个状态的值函数，利用该值函数和贪婪策略得到新的策略。如此循环下去，最终得到最优策略。

3.1.1 策略评估

对于模型已知强化学习算法，我们有状态-值函数：

$\small \nu_{\pi}(s)=\sum_{a \in A}\pi(a|s)(R_{s}^a+\gamma\sum_{s'\in S}P_{ss'}^a\nu_{\pi}(s'))$

其中，根据模型已知，状态转移概率 $\small P_{ss'}^a$ 、即时回报 $\small R_{s}^a$ 、折扣因子 $\small \gamma$ 已知，要评估的策略 $\small \pi(a|s)$ 是指定的，故只有值函数是未知的。问题转化为关于值函数的线性方程组，其未知数的个数为状态的总数。

（1）解析解

$\small \nu_{\pi}(s)=\sum_{a \in A}\pi(a|s)R_{s}^a+\gamma\sum_{s'\in S}\sum_{a \in A}\pi(a|s)P_{ss'}^a\nu_{\pi}(s'))$

$\small \sum_{a \in A}\pi(a|s)R_{s}^a\doteq r_{\pi}(s),\sum_{a \in A}\pi(a|s)P_{ss'}^a\doteq P_{\pi}(s,s')$

令 $\small s_{i}=s,s_{j}=s'$ ，则：

$\small \nu_{\pi}(s_{i})=r_{\pi}(s_{i})+\gamma\sum_{j=1}^{|s|}P_{\pi}(s_{i},s_{j})\nu_{\pi}(s_{j})$

写成矩阵形式为：

$\small \nu_{\pi}=r_{\pi}+\gamma P_{\pi}\nu_{\pi}$

$\small \nu_{\pi}=(I-\gamma P_{\pi})^{-1}r_{\pi}$

（2）迭代解

$\small \small \nu_{k+1}(s)=\sum_{a \in A}\pi(a|s)(R_{s}^a+\gamma\sum_{s'\in S}P_{ss'}^a\nu_{k}(s'))$

根据上式进行迭代，最终会收敛于 $\small \nu_{\pi}$ .

3.1.2 策略改进

利用策略评估得到的值函数，如何找到最优策略？一个自然的方法就是当已知当前策略的值函数时，在每个状态采用贪婪策略对当前策略进行改进：

$\small \pi_{l+1}(s) =\arg\max_{a}q^{\pi_{l}}(s,a)$

3.2 值函数迭代算法

策略迭代算法中，每一次策略改进都必须要等待策略评估中值函数收敛完毕才可以进行，事实上并不需要这么做。如果我们在评估一次之后就进行策略改善，则称为值函数迭代算法。

4 基于蒙特卡洛的强化学习方法

在动态规划的方法中，值函数的计算方法如下：

$\small \nu_{\pi}(s)=\sum_{a \in A}\pi(a|s)(R_{s}^a+\gamma\sum_{s'\in S}P_{ss'}^a\nu_{\pi}(s'))$

而在无模型的马尔科夫决策问题中，状态转移函数是未知的，因此要想利用策略评估和策略改进的方法，必须采用其他方法评估当前策略（计算值函数）。

由于状态-值函数和状态-行为值函数都是数学期望，动态规划的方法是利用模型来计算该期望，在无模型场合下，我们可以采用蒙特卡洛的方法计算该期望，即利用随机样本估计期望。

当要评估智能体的当前策略 $\small \pi$ 时，可以利用策略 $\small \pi$ 产生很多次试验，每次试验都是从任意的初始状态开始直到终止，得到一组试验数据，然后求平均值得到状态s处的值函数。

利用蒙特卡洛方法求状态s处的值函数时，可以分为第一次访问蒙特卡洛方法和每次访问蒙特卡洛方法。前者是指只利用每次试验中第一次访问到状态s时的返回值，后者是指利用所有访问到状态s时的回报返回值。

（1）蒙特卡洛策略改善

蒙特卡洛方法利用经验平均估计策略值函数。估计出值函数以后，对于每个状态s，它通过最大化动作值函数来进行策略的改善。即：

$\small \pi(s)=\arg\max_{a}q(s,a)$

（2）递增计算均值的方法

$\small \nu_{k}(s)=\frac{1}{k}\sum_{j=1}^{k}G_{j}(s) =\frac{1}{k}(G_{k}(s)+\sum_{j=1}^{k-1}G_{j}(s)) =\frac{1}{k}(G_{k}(s)+(k-1)\nu_{k-1}(s)) =\nu_{k-1}(s)+\frac{1}{k}(G_{k}(s)+\nu_{k-1}(s))$

为了保证值函数的收敛性，充分评估策略值函数，蒙特卡罗方法需要保证每个状态都能被访问到。

方法之一就是探索性初始化，即指每个状态都有一定的概率作为初始状态，这样可以保证迭代过程中每个状态行为都能被选中。

也可以通过精心选择探索策略，来保证在初始状态不变的同时，又能保证每个状态行为都可以被访问，比如采用温和策略，即对所有的状态s和a都满足： $\small \pi(a|s)>0$

5 基于时间差分的强化学习方法

蒙特卡洛方法需要等到每次试验结束，所以学习速度慢，效率低。时间差分方法结合了蒙特卡洛的采样方法（即试验）和动态规划的bootstrapping（利用后继状态的值函数估计当前之前）。

用时间差分方法（Temporal-Difference, TD）将值函数的公式更新为：

$\small V(S_{t})\leftarrow V(S_{t})+\alpha(R_{t+1}+\gamma V(S_{t+1})-V(S_{t}))$

与蒙特卡洛方法相比，时间差分方法只用到了一步随机状态和动作，随机性小，方差小。

时间差分方法包括同策略on-policy的Sarsa方法和异策略off-policy的Qlearning方法。

（1）Q-learning

$\small Initialize \,\,\,Q(s,a) \,\,\,arbitrarily$

$\small Repeat(for \, each \,episode):$

$\small Initialize \ s$

$\small Repeat(for \: each \: step \: of \: episode):$

$\small choose\, a\, from\, s\, using\, policy \,derived \,from\, Q(e.g.$ $\small \epsilon-greedy$ )

$\small Take \,action \,a, observe \,r, s'$

$\small Q(s,a)\leftarrow Q(s,a)+\alpha[r + \gamma \max_{a'}Q(s',a')-Q(s,a)]$

$\small s\leftarrow s'$

$\small until\,s\,is\,terminal$

（2）Sarsa

$\small Initialize \,\,\,Q(s,a) \,\,\,arbitrarily$

$\small Repeat(for \, each \,episode):$

$\small Initialize \ s$

$\small choose\, a\, from\, s\, using\, policy \,derived \,from\, Q(e.g.$ $\small \epsilon-greedy$ )

$\small Repeat(for \: each \: step \: of \: episode):$

$\small Take \,action \,a, observe \,r, s'$

$\small \small choose\, a'\, from\, s'\, using\, policy \,derived \,from\, Q(e.g.$ $\small \epsilon-greedy$ )

$\small \small Q(s,a)\leftarrow Q(s,a)+\alpha[r + \gamma Q(s',a')-Q(s,a)]$

$\small \small s\leftarrow s';a \leftarrow a'$

$\small until\,s\,is\,terminal$

6 基于值函数逼近的强化学习算法

6.1 基于值函数逼近的理论讲解

基于动态规划的方法、基于蒙特卡洛的方法以及基于时间差分的方法，都假设状态空间和动作空间是离散的，而且状态空间和动作空间不能太大。这些强化学习方法的基本步骤是先评估值函数，然后利用值函数改善当前的策略。其中值函数的评估是关键。

这时的值函数其实是一个表格。对于状态值函数，其索引是状态；对于行为值函数，其索引是状态-行为对。值函数的迭代更新实际上就是这张表的迭代更新。因此，上述强化学习算法又称为表格型强化学习。

若状态空间的维数很大，或者状态空间为连续空间，则此时的值函数无法用一张表格来表示。这时，需要利用值函数逼近的方法表示值函数，之后利用策略迭代和值迭代的方法构建强化学习方法。从数学的角度，函数逼近方法可以分为参数逼近和非参数逼近，因此强化学习值函数估计可以分为参数化逼近和非参数化逼近。其中，参数化逼近又分为线性参数化逼近和非线性参数化逼近。

当逼近的值函数结构确定时（如线性逼近时选定了基函数，非线性逼近时选定了神经网络的结构），那么值函数的逼近就等价于参数的逼近，值函数的更新就等价于参数的更新。

函数逼近 $\small \hat{v}(s,\theta)$ 的过程是一个监督学习的过程，其数据和标签对为 $\small (S_{t},U_{t})$ ,其中 $\small U_{t}$ 等价于蒙特卡洛方法中的 $\small G_{t}$ ，时间差分方法中 $\small r+\gamma Q(s',a')$ 的，训练的目标函数为：

$\small arg\min_{\theta}(q(a,s)-\hat{q}(s,a,\theta))^2$

值函数更新可以分为增量式学习方法和批学习方法。

（1）增量式学习方法：随机梯度下降法

参数的随机梯度更新为：

$\small \theta_{t+1}=\theta_{t}+\alpha[U_{t}-\hat{v}(S_{t},\theta_{t})]\triangledown_{\theta}\hat{v}(S_{t},\theta)$

基于蒙特卡罗方法的函数逼近的过程如下：

给定要评估的策略 $\small \pi$ ,产生一次试验： $\small s_{1},a_{1},s_{2},a_{2},...,s_{T-1},a_{T-1},s_{T}$

值函数的更新过程实际上是一个监督学习的过程，其中监督数据集从蒙特卡罗的试验数据中得到：其数据集为： $\small <s_{1},G_{1}>,<s_{2},G_{2}>,...,<s_{T},G_{T}>$

值函数的更新如下：

$\small \Delta \theta=\alpha[G_{t}-\hat{v}(S_{t},\theta)]\triangledown_{\theta}\hat{v}(S_{t},\theta)$

基于梯度的蒙特卡洛值函数评估算法

输入：要评估的策略 $\small \pi$ ，一个可微逼近函数 $\small \hat{v}$ ,恰当地初始化值函数权重 $\small \theta$

Repeat:

利用策略产生一幕数据

$\small For\, t=0,1,...,T-1$

$\small \small \theta \leftarrow \theta+\alpha[U_{t}-\hat{v}(S_{t},\theta)]\triangledown_{\theta}\hat{v}(S_{t},\theta)$

基于半梯度的TD(0)值函数评估算法

输入：要评估的策略 $\small \pi$ ，一个可微逼近函数 $\small \hat{v}$ ,恰当地初始化值函数权重 $\small \theta$

Repeat：

初始化状态S

Repeat（对于一幕中的每一步）

选择动作a

采用动作a并观测回报R,S'

$\small \small \theta_{t+1}=\theta_{t}+\alpha[R+\gamma\hat{v}(S',\theta)-\hat{v}(S_{t},\theta_{t})]\triangledown_{\theta}\hat{v}(S_{t},\theta)$

$\small S\leftarrow S'$

直到S'是中止状态

（2）批方法

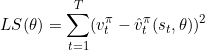所谓批的方法是指给定经验数据集 $\small D={<s_{1},v_{1}^{\pi}>,<s_{2},v_{2}^{\pi}>,...,<s_{T},v_{T}^{\pi}>}$ ,找到最好的拟合函数 $\small \hat{v}(s,\theta)$ ,使得 $\small LS(\theta)=\sum_{t=1}^{T}(v_{t}^{\pi}-\hat{v}_{t}^{\pi}(s_{t},\theta))^2$ 最小。可以使用最小二乘法进行求解。

6.2 DQN及其变形

6.2.1 DQN方法

DQN算法的大体框架是传统强化学习中的Qlearning

Qlearning方法是异策略时间差分方法，其算法步骤如下：

$\small Initialize \,\,\,Q(s,a) \,\,\,arbitrarily$

$\small Repeat(for \, each \,episode):$

$\small Initialize \ s$

$\small Repeat(for \: each \: step \: of \: episode):$

$\small choose\, a\, from\, s\, using\, policy \,derived \,from\, Q(e.g.$ $\small \epsilon-greedy$ )

$\small Take \,action \,a, observe \,r, s'$

$\small Q(s,a)\leftarrow Q(s,a)+\alpha[r + \gamma \max_{a'}Q(s',a')-Q(s,a)]$

$\small s\leftarrow s'$

$\small until\,s\,is\,terminal$

对于Qlearning的理解：

异策略：指的是行动策略（产生数据的策略）和要评估的策略不是一个策略。在算法中，行动策略是 $\small \epsilon-greedy$ 策略，要评估和改进的策略时贪婪策略。

时间差分方法：是指利用时间差分目标来更新当前行为值函数。在算法中，时间差分目标为 $\small r + \gamma \max_{a'}Q(s',a')$

DQN对Qlearning的改进体现在三个方面：

（1）DQN利用深度卷积神经网络逼近值函数

（2）DQN利用了经验回放训练强化学习的学习过程

（3）DQN独立设置了目标网络来单独处理时间差分算法中的TD偏差

（1）DQN利用深度卷积神经网络逼近值函数

DQN用神经网络逼近值函数属于参数化非线性逼近，值函数依然对应着一组参数，在神经网络里参数是每层网络的权重。更新值函数实际上是更新参数。DQN利用的网络结构是三个卷积层加两个全连接层.

（2）DQN利用了经验回放训练强化学习过程

经验回放是指在强化学习过程中，智能体将数据存储到一个数据库中，再利用均匀随机采样的方法从数据库中抽取数据，然后利用抽取的数据训练神经网络。这样可以打破数据之间的关联，从而使得训练得到的神经网络收敛且稳定。

（3）DQN独立设置了目标网络来单独处理时间差分算法中的TD偏差

在DQN算法之前，利用神经网络逼近值函数时，计算TD目标的动作值函数所用的网络参数 $\small \theta$ ，与梯度计算中要逼近的值函数所用的网络参数相同，这样就容易导致数据间存在关联性，从而使训练不稳定。为了解决这个问题，DQN将计算TD目标的网络表示为 $\small \theta^-$ ,计算值函数逼近的网络表示为 $\small \theta$ ，用于动作值函数逼近的网络每一步都更新，而用于计算TD目标的网络则是每个固定的步数更新一次。

因此，值函数的更新变为：

$\small \small \small \theta_{t+1}=\theta_{t}+\alpha[R+\gamma \max_{a'}{Q}(s',a';\theta^-)-\hat{Q}(s,a;\theta_{t})]\triangledown_{\theta}\hat{Q}(s,a;\theta)$

$\small DQN$ 算法伪代码：

$\small Initialize \ replay \ memeory \ D \ to \ capacity \ N$

$\small Initialize \ action-value \ function \ Q \ with \ random \ weight \ \theta$

$\small Initialize \ target \ action-value \ function \ Q \ with \ weight \ \theta^-=\theta$

$\small For \ episode \ =1,M \ do$

$\small Initialize \ sequence \ s_{1}={x_{1}} \ and \ preprocessed sequence \ \phi _{1}=\phi(s_{1})$

$\small For \ t = 1,T \ do$

$\small With \ probability \ \epsilon \ select \ a \ random \ action \ a_{t}$

$\small otherwise \ select \ a_{t}=argmax_{a}Q(\phi(s_{t}),a;\theta)$

$\small Execute \ a \ action \ a_{t} \ in \ emulator \ and \ observe \ reward \ r_{t} \ and \ image \ x_{t+1}$

$\small Set \ s_{t+1} =s_{t},a_{t},x_{t+1} \ and \ preprocess \ \phi_{t+1}=\phi(s_{t+1})$

$\small Store \ transition (\phi_{t},a_{t},r_{t},\phi_{t+1}) \ in \ D$

$\small Sample \ random minibatch \ of \ transitions \ (\phi_{j}, a_{j},r_{j},\phi_{j+1}) \ from \ D$

$\small if \ episode \ terminates \ at \ step \ j+1$

$\small Set \ y_{j} =r_{j}$

$\small else:$

$\small Set y_{j}= r_{j}+ \gamma max_{a'} \hat{Q}(\phi_{j+1},a'; \theta^{-})$

$\small Perform \ a \ gradient \ descent \ step \ on \ (y_{j}-Q(\phi_{j},a_{j};\theta))^2 \$

$\small with \ respect\ to \ the \ network \ parameters \ \theta$

$\small Every \ C \ step \ reset \ \theta^-=\theta$

$\small End \ for$

6.2.2 Double DQN

DQN的框架仍然是Qlearning，只是利用了卷积神经网络表示动作值函数，用经验回放和单独设立目标网络这两个技巧，但依然不能克服Qlearning本身的缺点：过估计。

Qlearning评估值函数的数学公式为：

对于表格型：

$\small Q(s,a)\leftarrow Q(s,a)+\alpha[r + \gamma \max_{a'}Q(s',a')-Q(s,a)]$

对于基于值函数逼近的方法：

$\small \small \small \theta_{t+1}=\theta_{t}+\alpha[R+\gamma \max_{a'}{Q}(s',a';\theta^-)-\hat{Q}(s,a;\theta_{t})]\triangledown_{\theta}\hat{Q}(s,a;\theta)$

可以看出值函数更新公式中都含有max操作，使得估计的值函数比值函数的真实值大。如果值函数每一点的值都被过估计了相同的幅度，即过估计量是均匀的，那么由于最优策略是贪婪策略，即找到大的值函数所对应的动作，这时候最优策略是保持不变的。也就是说，这种情况下即使值函数被过估计了，也不影响找到最优的策略。但实际情况中，过估计量并不一定是均匀的，因此过估计会影响到最优策略的选择。

为了解决值函数过估计的问题，Double Qlearning的方法被提出，即将动作的选择和动作的评估分别用不同的值函数来实现。

Double Qlearning的TD目标公式为：

$\small Y_{t}^{DoubleQ}=R_{t+1}+\gamma Q(S_{t+1},arg\max_{a}Q(S_{t+1},a;\theta_{t});\theta_{t}')$

将Double Qlearning的思想用到DQN中，则得到Double DQN，即Double DQN的TD目标为：

$\small Y_{t}^{DoubleQ}=R_{t+1}+\gamma Q(S_{t+1},arg\max_{a}Q(S_{t+1},a;\theta_{t}^-);)$

6.2.3 优先回放（Prioritized Replay）

DQN经验回放时利用均匀分布采样并不能有效利用数据，因为智能体在某些状态的学习效率比其他状态的学习效率高。优先回放的基本思想就是打破均匀采样，赋予学习效率高的状态更大的采样权重。

一种方法是，TD偏差越大，则说明该状态处的值函数与TD目标的差距越大，智能体的更新量越大，因此在此处的学习效率越高。设样本i处的TD偏差为 $\small \delta_{i}$ ,则该样本处的采样概率为：

$\small P(i)=\frac{p_{i}}{\sum_{k}p_{k}}$

其中， $\small p_{i}$ 由偏差 $\small \delta_{i}$ 决定，一种方法是 $\small p_{i}=|\delta_{i}|+\epsilon$ ,一种方法是 $\small p_{i}=\frac{1}{rank_{i}}$ ，其中 $\small rank_{i}$ 由偏差的 $\small \delta_{i}$ 的大小顺序决定。

当我们采用优先回放时的和概率分布采样时，动作值函数的估计值是一个有偏估计。因为采样分布与动作值函数的分布是两个完全不同的分布，为了校正这个偏差，需要乘以一个重要性采样系数 $\small w_{i}=(\frac{1}{N}\frac{1}{P(i)})^\beta$

6.2.4 Dueling DQN

前面几种DQN算法在值函数逼近时所用的神经网络都是卷积神经网络。Dueling DQN则是从网络结构上进行了改进。动作值函数可以分解为状态值函数和优势函数，即：

$\small Q^\pi(s,a)=V^\pi(s)+A^\pi(s,a)$

前面几种方法都是用神经网络直接逼近 $\small Q^\pi(s,a)$ ，而Dueling DQN则是用神经网络分别逼近 $\small V^\pi(s)$ 和 $\small A^\pi(s,a)$ 。

7.基于直接策略搜索的强化学习方法

7.1 基于策略梯度的强化学习方法

在值函数的方法中，我们迭代计算的是值函数，再根据值函数改善策略；而在策略搜索方法中，我们直接对策略进行迭代计算，也就是迭代更新策略的参数值，直到累计回报的期望最大，此时的参数所对应的策略为最优策略。

策略搜索是将策略参数化，即 $\small \pi_{\theta}(s)$ :利用参数化的线性函数或非线性函数（如神经网络）表示策略，寻找最优的参数 $\small \theta$ ,使强化学习的目标——累计回报的期望 $\small E[\sum_{t=0}^{H}R(S_{t}|\pi_{\theta})]$ 最大。

策略搜索方法按照是否利用模型可分为无模型的策略搜索方法和有模型的策略搜索方法。其中无模型的策略搜索方法根据策略是采用随机策略还是确定性策略分为随机策略搜素方法和确定性策略搜索方法。随机策略搜索方法中最先发展起来的是策略梯度方法。

下面我们从似然率的角度推导策略梯度

7.2 基于置信域策略优化的强化学习方法

根据策略梯度的方法，参数更新公式为:

$\small \theta_{new}=\theta_{old}+\alpha\triangledown _{\theta}J$

策略梯度算法的难点在于更新步长 $\small \alpha$ 的选择，当步长不合适的时候，更新的参数所对应的策略是一个更不好的策略，当利用这个更不好的策略采样学习时，再次更新参数往往会导致更差的结果。所以，合适的步长非常重要。

TRPO（Trust Region Policy Optimization）置信域策略优化可以找到新的策略使新的回报函数的值单调增长，或者单调不减。

你可能感兴趣的:(算法,强化学习)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列 C语言
文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
[Python] 数据结构详解及代码 AIAdvocate 算法 python 数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
Python算法L5：贪心算法小熊同学哦 Python算法算法 python 贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
【RabbitMQ 项目】服务端：数据管理模块之绑定管理月夜星辉雪 rabbitmq 分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
非对称加密算法原理与应用2——RSA私钥加密文件私语茶馆云部署与开发架构及产品灵感记录 RSA2048 私钥加密
作者：私语茶馆1.相关章节（1）非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对，并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容，包括从密钥库或文件中读取私钥，并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件，只能由该私钥对应的公钥来解密。
粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能 matlab 算法
在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
非对称加密算法————RSA理论及详情 hu19930613
转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
【加密算法基础——对称加密和非对称加密】 XWWW668899 网络安全服务器笔记
对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法，各自有不同的特点和用途。以下是详细比较：1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快，适合处理大量数据。实现:算法相对简单，计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
【算法练习】IDEA集成leetcode插件实现快速刷 2401_84102892 2024年程序员学习算法 intellij-idea leetcode
============点击右侧边leetcode->设置->配置地址、用户名、密码、存放目录、文件模板用户名要登录后在账号信息里看模板代码1.codefilename!velocityTool.camelC
【加密算法基础——RSA 加密】 XWWW668899 网络服务器笔记 python
RSA加密RSA（Rivest-Shamir-Adleman）加密是非对称加密，一种广泛使用的公钥加密算法，主要用于安全数据传输。公钥用于加密，私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏：R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法，并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础，使得安全通
机器学习-聚类算法不良人龍木木机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记，感谢点赞关注！1.AHC2.K-means3.SC传统谱聚类：个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持！
生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
高性能javascript--算法和流程控制海淀萌狗
-for,while和do-while性能相当-避免使用for-in循环，==除非遍历一个属性量未知的对象==es5:for-in遍历的对象便不局限于数组，还可以遍历对象。原因：for-in每次迭代操作会同时搜索实例或者原型属性，for-in循环的每次迭代都会产生更多开销，因此要比其他循环类型慢，一般速度为其他类型循环的1/7。因此，除非明确需要迭代一个属性数量未知的对象，否则应避免使用for-i
深度 Qlearning：在直播推荐系统中的应用 AGI通用人工智能之禅程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据 AIGC AGI LLM Java Python 架构设计 Agent 程序员实现财富自由
深度Q-learning：在直播推荐系统中的应用关键词：深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
JVM源码分析之堆外内存完全解读 HeapDump性能社区
概述广义的堆外内存说到堆外内存，那大家肯定想到堆内内存，这也是我们大家接触最多的，我们在jvm参数里通常设置-Xmx来指定我们的堆的最大值，不过这还不是我们理解的Java堆，-Xmx的值是新生代和老生代的和的最大值，我们在jvm参数里通常还会加一个参数-XX:MaxPermSize来指定持久代的最大值，那么我们认识的Java堆的最大值其实是-Xmx和-XX:MaxPermSize的总和，在分代算法
《算法》四学习——1.1节进阶的Farmer 算法算法笔记
前言买了一本算法4，每天看一点，对每个小结来个学习总结，输出驱动输入。本篇笔记针对第一章基础1.1基础编程模型1.1节总结了相关的语法、语言特性和书中将会用到的库。笔记自己在编码中容易遗漏的点&&优先级比||高在开发中习惯了加括号，所以没注意到这点，教材上也有但是忘记了二分查找中计算mid=left+(right-left)/2这样计算可以有效避免(left+right)/2溢出答疑java无穷大
排序路小白同学
1.冒泡排序冒泡算法是一种基础的排序算法，这种算法会重复的比较数组中相邻的两个元素。如果一个元素比另一个元素大（小），那么就交换这两个元素的位置。重复这一比较直至最后一个元素。这一比较会重复n-1趟，每一趟比较n-j次，j是已经排序好的元素个数。每一趟比较都能找出未排序元素中最大或者最小的那个数字。这就如同水泡从水底逐个飘到水面一样。冒泡排序是一种时间复杂度较高，效率较低的排序方法。其空间复杂度是
算法单链的创建与删除换个号韩国红果果 c 算法
先创建结构体 struct student { int data; //int tag;//标记这是第几个 struct student *next; }; // addone 用于将一个数插入已从小到大排好序的链中 struct student *addone(struct student *h,int x){ if(h==NULL) //??????
《大型网站系统与Java中间件实践》第2章读后感白糖_ java中间件
断断续续花了两天时间试读了《大型网站系统与Java中间件实践》的第2章，这章总述了从一个小型单机构建的网站发展到大型网站的演化过程---整个过程会遇到很多困难，但每一个屏障都会有解决方案，最终就是依靠这些个解决方案汇聚到一起组成了一个健壮稳定高效的大型系统。看完整章内容，
zeus持久层spring事务单元测试 deng520159 java DAO spring jdbc
今天把zeus事务单元测试放出来,让大家指出他的毛病, 1.ZeusTransactionTest.java 单元测试 package com.dengliang.zeus.webdemo.test; import java.util.ArrayList; import java.util.List; import org.junit.Test; import
Rss 订阅开发周凡杨 html xml 订阅 rss 规范
RSS是 Really Simple Syndication的缩写（对rss2.0而言，是这三个词的缩写，对rss1.0而言则是RDF Site Summary的缩写，1.0与2.0走的是两个体系）。 RSS
分页查询实现 g21121 分页查询
在查询列表时我们常常会用到分页，分页的好处就是减少数据交换，每次查询一定数量减少数据库压力等等。按实现形式分前台分页和服务器分页：前台分页就是一次查询出所有记录，在页面中用js进行虚拟分页，这种形式在数据量较小时优势比较明显，一次加载就不必再访问服务器了，但当数据量较大时会对页面造成压力，传输速度也会大幅下降。服务器分页就是每次请求相同数量记录，按一定规则排序，每次取一定序号直接的数据
spring jms异步消息处理 510888780 jms
spring JMS对于异步消息处理基本上只需配置下就能进行高效的处理。其核心就是消息侦听器容器，常用的类就是DefaultMessageListenerContainer。该容器可配置侦听器的并发数量，以及配合MessageListenerAdapter使用消息驱动POJO进行消息处理。且消息驱动POJO是放入TaskExecutor中进行处理，进一步提高性能，减少侦听器的阻塞。具体配置如下：
highCharts柱状图布衣凌宇 hightCharts 柱图
第一步：导入 exporting.js,grid.js,highcharts.js;第二步：写controller @Controller@RequestMapping(value="${adminPath}/statistick")public class StatistickController { private UserServi
我的spring学习笔记2-IoC（反向控制依赖注入） aijuans spring mvc Spring 教程 spring3 教程 Spring 入门
IoC（反向控制依赖注入）这是Spring提出来了，这也是Spring一大特色。这里我不用多说，我们看Spring教程就可以了解。当然我们不用Spring也可以用IoC，下面我将介绍不用Spring的IoC。 IoC不是框架，她是java的技术，如今大多数轻量级的容器都会用到IoC技术。这里我就用一个例子来说明：如：程序中有 Mysql.calss 、Oracle.class 、SqlSe
TLS java简单实现 antlove java ssl keystore tls secure
1. SSLServer.java package ssl; import java.io.FileInputStream; import java.io.InputStream; import java.net.ServerSocket; import java.net.Socket; import java.security.KeyStore; import
Zip解压压缩文件百合不是茶 Zip格式解压 Zip流的使用文件解压
ZIP文件的解压缩实质上就是从输入流中读取数据。Java.util.zip包提供了类ZipInputStream来读取ZIP文件,下面的代码段创建了一个输入流来读取ZIP格式的文件; ZipInputStream in = new ZipInputStream(new FileInputStream(zipFileName)); &n
underscore.js 学习（一） bijian1013 JavaScript underscore
工作中需要用到underscore.js，发现这是一个包括了很多基本功能函数的js库，里面有很多实用的函数。而且它没有扩展 javascript的原生对象。主要涉及对Collection、Object、Array、Function的操作。学
java jvm常用命令工具——jstatd命令(Java Statistics Monitoring Daemon) bijian1013 java jvm jstatd
1.介绍 jstatd是一个基于RMI（Remove Method Invocation）的服务程序，它用于监控基于HotSpot的JVM中资源的创建及销毁，并且提供了一个远程接口允许远程的监控工具连接到本地的JVM执行命令。 jstatd是基于RMI的，所以在运行jstatd的服务
【Spring框架三】Spring常用注解之Transactional bit1129 transactional
Spring可以通过注解@Transactional来为业务逻辑层的方法(调用DAO完成持久化动作)添加事务能力，如下是@Transactional注解的定义： /* * Copyright 2002-2010 the original author or authors. * * Licensed under the Apache License, Version
我(程序员)的前进方向 bitray 程序员
作为一个普通的程序员,我一直游走在java语言中,java也确实让我有了很多的体会.不过随着学习的深入,java语言的新技术产生的越来越多,从最初期的javase,我逐渐开始转变到ssh,ssi,这种主流的码农,.过了几天为了解决新问题,webservice的大旗也被我祭出来了,又过了些日子jms架构的activemq也开始必须学习了.再后来开始了一系列技术学习,osgi,restful.....
nginx lua开发经验总结 ronin47
使用nginx lua已经两三个月了，项目接开发完毕了，这几天准备上线并且跟高德地图对接。回顾下来lua在项目中占得必中还是比较大的，跟PHP的占比差不多持平了，因此在开发中遇到一些问题备忘一下 1：content_by_lua中代码容量有限制，一般不要写太多代码，正常编写代码一般在100行左右（具体容量没有细心测哈哈，在4kb左右），如果超出了则重启nginx的时候会报 too long pa
java-66-用递归颠倒一个栈。例如输入栈{1,2,3,4,5}，1在栈顶。颠倒之后的栈为{5,4,3,2,1}，5处在栈顶 bylijinnan java
import java.util.Stack; public class ReverseStackRecursive { /** * Q 66.颠倒栈。 * 题目：用递归颠倒一个栈。例如输入栈{1,2,3,4,5}，1在栈顶。 * 颠倒之后的栈为{5,4,3,2,1}，5处在栈顶。 *1. Pop the top element *2. Revers
正确理解Linux内存占用过高的问题 cfyme linux
Linux开机后，使用top命令查看，4G物理内存发现已使用的多大3.2G，占用率高达80%以上： Mem: 3889836k total, 3341868k used, 547968k free, 286044k buffers Swap: 6127608k total,&nb
[JWFD开源工作流]当前流程引擎设计的一个急需解决的问题 comsci 工作流
当我们的流程引擎进入IRC阶段的时候，当循环反馈模型出现之后，每次循环都会导致一大堆节点内存数据残留在系统内存中，循环的次数越多，这些残留数据将导致系统内存溢出，并使得引擎崩溃。。。。。。而解决办法就是利用汇编语言或者其它系统编程语言，在引擎运行时，把这些残留数据清除掉。
自定义类的equals函数 dai_lm equals
仅作笔记使用 public class VectorQueue { private final Vector<VectorItem> queue; private class VectorItem { private final Object item; private final int quantity; public VectorI
Linux下安装R语言 datageek R语言 linux
命令如下：sudo gedit /etc/apt/sources.list1、deb http://mirrors.ustc.edu.cn/CRAN/bin/linux/ubuntu/ precise/ 2、deb http://dk.archive.ubuntu.com/ubuntu hardy universesudo apt-key adv --keyserver ke
如何修改mysql 并发数(连接数)最大值 dcj3sjt126com mysql
MySQL的连接数最大值跟MySQL没关系，主要看系统和业务逻辑了方法一：进入MYSQL安装目录打开MYSQL配置文件 my.ini 或 my.cnf查找 max_connections=100 修改为 max_connections=1000 服务里重起MYSQL即可　　方法二：MySQL的最大连接数默认是100客户端登录：mysql -uusername -ppass
单一功能原则 dcj3sjt126com 面向对象的程序设计软件设计编程原则
单一功能原则[ 编辑] SOLID 原则单一功能原则开闭原则 Liskov代换原则接口隔离原则依赖反转原则查论编在面向对象编程领域中，单一功能原则（Single responsibility principle）规定每个类都应该有
POJO、VO和JavaBean区别和联系 fanmingxing VO POJO javabean
POJO和JavaBean是我们常见的两个关键字，一般容易混淆，POJO全称是Plain Ordinary Java Object / Plain Old Java Object，中文可以翻译成：普通Java类，具有一部分getter/setter方法的那种类就可以称作POJO，但是JavaBean则比POJO复杂很多，JavaBean是一种组件技术，就好像你做了一个扳子，而这个扳子会在很多地方被
SpringSecurity3.X--LDAP：AD配置 hanqunfeng SpringSecurity
前面介绍过基于本地数据库验证的方式，参考http://hanqunfeng.iteye.com/blog/1155226，这里说一下如何修改为使用AD进行身份验证【只对用户名和密码进行验证，权限依旧存储在本地数据库中】。将配置文件中的如下部分删除：
mac mysql 修改密码 IXHONG mysql
$ sudo /usr/local/mysql/bin/mysqld_safe –user=root & //启动MySQL(也可以通过偏好设置面板来启动)$ sudo /usr/local/mysql/bin/mysqladmin -uroot password yourpassword //设置MySQL密码（注意，这是第一次MySQL密码为空的时候的设置命令，如果是修改密码，还需在-
设计模式--抽象工厂模式 kerryg 设计模式
抽象工厂模式：工厂模式有一个问题就是，类的创建依赖于工厂类，也就是说，如果想要拓展程序，必须对工厂类进行修改，这违背了闭包原则。我们采用抽象工厂模式，创建多个工厂类，这样一旦需要增加新的功能，直接增加新的工厂类就可以了，不需要修改之前的代码。总结：这个模式的好处就是，如果想增加一个功能，就需要做一个实现类，
评"高中女生军训期跳楼” nannan408
首先，先抛出我的观点，各位看官少点砖头。那就是，中国的差异化教育必须做起来。孔圣人有云：有教无类。不同类型的人，都应该有对应的教育方法。目前中国的一体化教育，不知道已经扼杀了多少创造性人才。我们出不了爱迪生，出不了爱因斯坦，很大原因，是我们的培养思路错了，我们是第一要“顺从”。如果不顺从，我们的学校，就会用各种方法，罚站，罚写作业，各种罚。军
scala如何读取和写入文件内容？ qindongliang1922 java jvm scala
直接看如下代码： package file import java.io.RandomAccessFile import java.nio.charset.Charset import scala.io.Source import scala.reflect.io.{File, Path} /** * Created by qindongliang on 2015/
C语言算法之百元买百鸡 qiufeihu c 算法
中国古代数学家张丘建在他的《算经》中提出了一个著名的“百钱买百鸡问题”，鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一，百钱买百鸡，问翁，母，雏各几何？代码如下： #include <stdio.h> int main() { int cock,hen,chick; /*定义变量为基本整型*/ for(coc
Hadoop集群安全性：Hadoop中Namenode单点故障的解决方案及详细介绍AvatarNode wyz2009107220 NameNode
正如大家所知，NameNode在Hadoop系统中存在单点故障问题，这个对于标榜高可用性的Hadoop来说一直是个软肋。本文讨论一下为了解决这个问题而存在的几个solution。 1. Secondary NameNode 原理：Secondary NN会定期的从NN中读取editlog，与自己存储的Image进行合并形成新的metadata image 优点：Hadoop较早的版本都自带，