[翻译+笔记]生成对抗网络: 从GAN到WGAN
最近读了一篇社会力模型的论文, 里面用到了GAN, 发现自己不是很懂. 想翻译一下一个大神的博客, 做一下笔记. 并不是全文翻译, 只翻译一部分.
原文地址: from GAN to WGAN
1. K-L和J-S散度
在介绍GAN之前, 首先复习一下衡量两个概率分布相似度的两种指标.
(1) K-L散度: KL散度衡量了某个概率分布 p p p是取自(发散自, 来自)另一个期望的(理论的)概率分布 q q q的程度:
D K L ( p ∣ ∣ q ) = ∫ x p ( x ) log p ( x ) q ( x ) d x D_{KL}(p||q)=\int_xp(x)\log{\frac{p(x)}{q(x)}}dx DKL(p∣∣q)=∫xp(x)logq(x)p(x)dx
当 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)处处相等时, KL散度为0.
我们要注意到KL散度是非对称的( D K L ( p ∣ ∣ q ) ≠ D K L ( q ∣ ∣ p ) D_{KL}(p||q) \ne D_{KL}(q||p) DKL(p∣∣q)=DKL(q∣∣p)), 而且当 p ( x ) p(x) p(x)接近0的时候, q ( x ) q(x) q(x)的作用就被忽略了. 这会在有时候造成很有问题的结果.
KL散度的本质就是互信息, 衡量两个概率分布的差别.
(2) J-S散度: JS散度是另一种衡量两个概率分布相似度的指标, 范围在 [ 0 , 1 ] [0,1] [0,1]之间. JS散度是对称的, 而且更平滑. 定义如下:
D J S ( p ∣ ∣ q ) = 1 2 D K L ( p ∣ ∣ p + q 2 ) + 1 2 D K L ( q ∣ ∣ p + q 2 ) D_{JS}(p||q)=\frac{1}{2}D_{KL}(p||\frac{p+q}{2})+\frac{1}{2}D_{KL}(q||\frac{p+q}{2}) DJS(p∣∣q)=21DKL(p∣∣2p+q)+21DKL(q∣∣2p+q)
二者差别如下图所示:
![[翻译+笔记]生成对抗网络: 从GAN到WGAN_第1张图片](http://img.e-com-net.com/image/info8/40a6389e004d438291c5037b6f54d841.jpg)
一些人认为GAN取得重大成功的原因之一是将损失函数从在极大似然方法中使用非对称的KL散度转成使用对称的JS散度.
2. 生成对抗网络GAN
GAN由两部分模型组成:
- 一个鉴别器D, 其用来估计一个给定的样本来自于真实数据集的概率. 它相当于一个评论者, 它被优化的目标是在真实的样本中区分出假的样本.
- 一个生成器G, 其输出虚假的样本(虚假意为并非来自真实数据集), 以噪声变量z为输入(z带来了潜在的输出多样性). 它被训练的目标是获取真实的数据分布以使得产生的样本更可能接近于真实的分布, 换句话说, 可以欺骗鉴别器, 让鉴别器以高概率认为是真实的样本.
![[翻译+笔记]生成对抗网络: 从GAN到WGAN_第2张图片](http://img.e-com-net.com/image/info8/476b473f192b47ebb093628f9bc9e0a5.jpg)
这两个模型在训练过程中互相竞争: 生成器G努力去欺骗鉴别器D, 但鉴别器也努力不被欺骗. 这种有趣的零和博弈会促使两部分提高他们各自的功能.
假定以下符号:
| p z p_z pz | 噪声输入z的数据分布 |
| p g p_g pg | 生成器关于数据x的(输出)分布 |
| p r p_r pr | 真实样本x的分布 |
一方面, 我们想确保鉴别器D对于真实的数据的决定是非常精确的, 也就是最大化 E x ∼ p r ( x ) [ log D ( x ) ] E_{x\sim p_r(x)}[\log D(x)] Ex∼pr(x)[logD(x)], 也就是说, 让 D ( x ) D(x) D(x)尽可能接近1. 同时, 给定一个假样本 G ( z ) G(z) G(z), 鉴别器会输出一个概率 D ( G ( z ) ) D(G(z)) D(G(z)), 我们也希望鉴别器让这个概率接近0, 因此等价于最大化 E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ] E_{z\sim p_z(z)}[\log (1-D(G(z))] Ez∼pz(z)[log(1−D(G(z))].
另一方面, 生成器的目标是增大自己产生的样本被鉴别器识别为真实样本的概率, 也就是最小化 E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ] E_{z\sim p_z(z)}[\log (1-D(G(z))] Ez∼pz(z)[log(1−D(G(z))].
我们把两个方面都考虑进去, D和G就是玩了一个最大-最小游戏, 我们应该优化如下的损失函数:
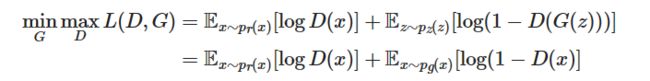
之所以可以将第一项 E x ∼ p r ( x ) [ log D ( x ) ] E_{x\sim p_r(x)}[\log D(x)] Ex∼pr(x)[logD(x)]也算入生成器的优化过程, 是因为其相当于常数项, 并不产生影响.
D的最佳值是什么?
我们现在有了一个定义良好的损失函数. 现在我们看看D的最佳值是什么.
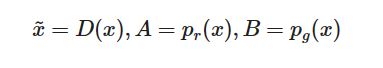
之后, 在积分里面的项为(我们可以安全地忽略积分, 因为 x x x是从所有可能取值中采样的):
D ∗ ( x ) = x ~ ∗ = A A + B = p r ( x ) p r ( x ) + p g ( x ) D^*(x)=\tilde{x}^*=\frac{A}{A+B}=\frac{p_r(x)}{p_r(x)+p_g(x)} D∗(x)=x~∗=A+BA=pr(x)+pg(x)pr(x).
我们当然希望生成器输出的概率分布 p g ( x ) p_g(x) pg(x)能与 p r ( x ) p_r(x) pr(x)十分接近, 此时 D ∗ ( x ) = 1 / 2 D^*(x)=1/2 D∗(x)=1/2(鉴别器相当于在瞎猜).
全局最优是什么?
当G和D都到达了最优的值, 也就是 p g ( x ) = p r ( x ) p_g(x)=p_r(x) pg(x)=pr(x), D ∗ ( x ) = 1 / 2 D^*(x)=1/2 D∗(x)=1/2, 损失函数变为:
![[翻译+笔记]生成对抗网络: 从GAN到WGAN_第4张图片](http://img.e-com-net.com/image/info8/bb678eb676f24399badcccdc98c12e39.jpg)
因此GAN损失函数的理论下界为 − 2 log 2 -2\log2 −2log2.
损失函数代表了什么?
我们展开J-S散度:
D J S ( p ∣ ∣ q ) = 1 2 D K L ( p ∣ ∣ p + q 2 ) + 1 2 D K L ( q ∣ ∣ p + q 2 ) = 1 2 [ ∫ x p ( x ) log p ( x ) ( p ( x ) + q ( x ) ) / 2 d x + ∫ x q ( x ) log q ( x ) ( p ( x ) + q ( x ) ) / 2 d x ] D_{JS}(p||q)=\frac{1}{2}D_{KL}(p||\frac{p+q}{2})+\frac{1}{2}D_{KL}(q||\frac{p+q}{2}) \\ =\frac{1}{2}[\int_xp(x)\log{\frac{p(x)}{(p(x)+q(x))/2}}dx+\int_xq(x)\log{\frac{q(x)}{(p(x)+q(x))/2}}dx]\\ DJS(p∣∣q)=21DKL(p∣∣2p+q)+21DKL(q∣∣2p+q)=21[∫xp(x)log(p(x)+q(x))/2p(x)dx+∫xq(x)log(p(x)+q(x))/2q(x)dx]
其中
∫ x p ( x ) log p ( x ) ( p ( x ) + q ( x ) ) / 2 d x = ∫ x p ( x ) log p ( x ) p ( x ) + q ( x ) d x + ∫ x p ( x ) log 2 d x = log 2 + ∫ x p ( x ) log p ( x ) p ( x ) + q ( x ) d x \int_xp(x)\log{\frac{p(x)}{(p(x)+q(x))/2}}dx=\int_xp(x)\log{\frac{p(x)}{p(x)+q(x)}}dx+\int_xp(x)\log{2}dx\\ =\log2 +\int_xp(x)\log{\frac{p(x)}{p(x)+q(x)}}dx ∫xp(x)log(p(x)+q(x))/2p(x)dx=∫xp(x)logp(x)+q(x)p(x)dx+∫xp(x)log2dx=log2+∫xp(x)logp(x)+q(x)p(x)dx
另一部分同理, 代入得
D J S ( p ∣ ∣ q ) = 1 2 [ 2 log 2 + ∫ x p ( x ) log p ( x ) p ( x ) + q ( x ) + ∫ x q ( x ) log q ( x ) p ( x ) + q ( x ) ] D_{JS}(p||q)=\frac{1}{2}[2\log2+\int_xp(x)\log{\frac{p(x)}{p(x)+q(x)}}+\int_xq(x)\log{\frac{q(x)}{p(x)+q(x)}}] DJS(p∣∣q)=21[2log2+∫xp(x)logp(x)+q(x)p(x)+∫xq(x)logp(x)+q(x)q(x)]
当 D D D达到最优值即 D ∗ ( x ) = p r ( x ) p r ( x ) + p g ( x ) D^*(x)=\frac{p_r(x)}{p_r(x)+p_g(x)} D∗(x)=pr(x)+pg(x)pr(x)时, 损失函数为
L ( G , D ∗ ) = ∫ x p r ( x ) log p r ( x ) p r ( x ) + p g ( x ) + ∫ x p g ( x ) log p g ( x ) p r ( x ) + p g ( x ) L(G,D^*)=\int_xp_r(x)\log{\frac{p_r(x)}{p_r(x)+p_g(x)}}+\int_xp_g(x)\log{\frac{p_g(x)}{p_r(x)+p_g(x)}} L(G,D∗)=∫xpr(x)logpr(x)+pg(x)pr(x)+∫xpg(x)logpr(x)+pg(x)pg(x)
令 p = p r ( x ) , q = p g ( x ) p=p_r(x), q=p_g(x) p=pr(x),q=pg(x), 代入得
D J S ( p r ∣ ∣ p g ) = 1 2 [ 2 log 2 + L ( G , D ∗ ) ] D_{JS}(p_r||p_g)=\frac{1}{2}[2\log 2+L(G,D^*)] DJS(pr∣∣pg)=21[2log2+L(G,D∗)]
所以
L ( G , D ∗ ) = 2 D J S ( p r ∣ ∣ p g ) − 2 log 2 L(G,D^*)=2D_{JS}(p_r||p_g)-2\log 2 L(G,D∗)=2DJS(pr∣∣pg)−2log2
所以当一切达到最优的时候, JS散度是0, 损失函数到达理论下界 − 2 log 2 -2\log 2 −2log2.
3. GAN中存在的问题
难以达到纳什均衡(Nash equilibrium)
训练过程中两个模型(G和D)是非合作博弈, 各自达到各自的平衡点, 不会考虑另一个模型. 因此并不能保证模型最终可以收敛.
以一个简单的例子说明为什么在非合作博弈中很难寻找纳什均衡. 假设一个玩家的目标是 f 1 ( x ) = x y f_1(x)=xy f1(x)=xy, 另一个玩家的目标是 f 2 ( y ) = − x y f_2(y)=-xy f2(y)=−xy, 则根据梯度下降法, 玩家1每次的更新策略为 x ← x − η y x\leftarrow x-\eta y x←x−ηy, 玩家2的策略为 y ← y + η x y\leftarrow y+\eta x y←y+ηx, 因此二者的方向是相反的. 更新过程如下图所示.
低维度的支持
有人认为许多真实数据集的维度只是人为提高. 例如含有狗的图片, 两个耳朵一个尾巴可以代表狗, 实际上不需要很多自由的高维形式. 也就是说复杂的东西可以集中在低维流形中.
p g p_g pg也位于低维流形中, 例如输入是100维的向量, 要获取64x64的图像, 这4096像素上的颜色分布已经由100维小随机数向量定义,几乎无法填满整个高维空间. 因为鉴别器和生成器都在低维流形中,它们几乎肯定会不相交(如图, 低维流形很难在高维空间填充). 当它们具有不相交的支撑时,我们总是能够找到一个完美的鉴别器,可以 100% 正确地区分真假样本.
![[翻译+笔记]生成对抗网络: 从GAN到WGAN_第6张图片](http://img.e-com-net.com/image/info8/f7c998ed2f1448f085f9983d33d05af0.jpg)
梯度消失
如果鉴别器非常完美, 即对每个真实样本都输出概率1, 每个虚假样本都输出概率0, 则损失函数会变为常数0, 梯度不再更新. 下图表明了当鉴别器变好的时候, 梯度在逐渐消失.
- 如果鉴别器很差, 那么生成器并没有精确的反馈, 损失函数不能代表真实情况
- 如果鉴别器很好, 那么损失函数就会很低, 学习就会很慢.
模式崩溃
在训练期间,生成器可能会折叠到始终产生相同输出的设置。这是 GAN 的常见故障情况,通常称为模式崩溃. 尽管生成器可能能够欺骗相应的鉴别器,但它无法学习表示复杂的真实世界数据分布,并且被困在一个种类极低的小空间.
缺少评估指标
生成对抗网络并不是天生就有良好的反对函数,可以通知我们训练进度. 如果没有一个好的评估指标,就像在黑暗中工作一样. 没有好的迹象可以告诉何时停止; 没有很好的指标来比较多个模型的性能.
4. 提升GAN的训练
(1) 特征匹配
特征匹配建议在优化鉴别器的时候, 让鉴别器检查生成器的输出是否符合真实样本的期望统计量, 也就是损失函数变为
∣ E x ∼ p r ( x ) [ f ( x ) ] − E z ∼ p z ( z ) [ f ( G ( z ) ] ∣ 2 2 |E_{x\sim p_r(x)}[f(x)] - E_{z\sim p_z(z)}[f(G(z)]|_2^2 ∣Ex∼pr(x)[f(x)]−Ez∼pz(z)[f(G(z)]∣22
其中 f f f可以是任何的特征的统计量, 例如均值或者中位数.
(2)minibatch判别
通过minibatch判别,鉴别器能够在一个batch中消化训练数据点之间的关系, 而不是独立处理每个点.
(3) 历史平均
将模型参数的历史平均和当前模型参数的差加入到损失函数, 即加入 ∣ Θ − 1 t ∑ i Θ i ∣ 2 |\Theta-\frac{1}{t}\sum_i \Theta_i|^2 ∣Θ−t1∑iΘi∣2, Θ \Theta Θ为参数. 这样可以平滑参数的变化.
(4) 单边标签平滑
馈送鉴别器时,不要提供 1 和 0 标签,而是使用 0.9 和 0.1 等软化值. 它被证明可以减少网络的脆弱性.
(5) 虚拟批归一化
就是用某一个固定的batch(成为参考batch)做批归一化, 而不是采用每次的minibatch. 参考batch在开始时选择一次,并在整个训练过程中保持不变.
(6) 加噪
根据前面的讨论, 我们知道 p r p_r pr和 p g p_g pg在高维空间不相交, 因此可以认为加噪使得他们"扩散".
(7) 对分布的相似度采用更好的指标
当两个分布不相交时,传统的损失函数无法提供有意义的值。
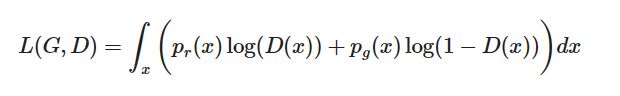
![[翻译+笔记]生成对抗网络: 从GAN到WGAN_第3张图片](http://img.e-com-net.com/image/info8/26504fa222b44b3c81bd3d7f5af71c51.jpg)
![[翻译+笔记]生成对抗网络: 从GAN到WGAN_第5张图片](http://img.e-com-net.com/image/info8/775f2c633e6c42b4a22f442a5ce6926a.jpg)
![[翻译+笔记]生成对抗网络: 从GAN到WGAN_第7张图片](http://img.e-com-net.com/image/info8/f971328d58c34233804b9b7ff008e892.jpg)