【LeetCode】图解KMP算法
文章目录
-
- 前言
- 1、简介
- 2、图解KMP思想
-
- 2.1、串的匹配
- 2.2、寻找相同前后缀
- 3、真枪实战
-
- 3.1、题目描述
- 3.2、示例
- 3.3、提示
- 3.4、思路
- 3.5、具体实现
- 3.6、测试结果
前言
思路和代码借鉴:https://github.com/mission-peace/interview/blob/master/src/com/interview/string/SubstringSearch.java
1、简介
KMP算法是由Knuth、Morris和Pratt同时设计实现的,该算法可以在 O(m+n) 的时间数量级上完成串的模式匹配操作。
相对于暴力破解,其好处在于:每当一趟匹配过程中字符比较不等时,指针不需要再次回溯,而是利用已经得到的“部分匹配”的结果将模式串向右“滑动”尽可能远的一段距离后,继续进行比较。
废话少说,就是KMP算法在串的模式匹配相关问题中有很广泛的应用,能够在极小的代价中得出主串与模式串匹配的结果。
主串与模式串理解和关系:
- 主串:给定的一串字符串,如
abxabcabcaby;- 模式串:也称子串,用于和主串进行匹配,一般长度不大于主串,否则匹配无意义,如
abcabyKMP算法为我们做的就是在主串中找到是否存在指定的模式串,即判断模式串是否为主串的子串,也可求得相匹配的模式串中的第一个字符在主串中出现的位置。
2、图解KMP思想
2.1、串的匹配
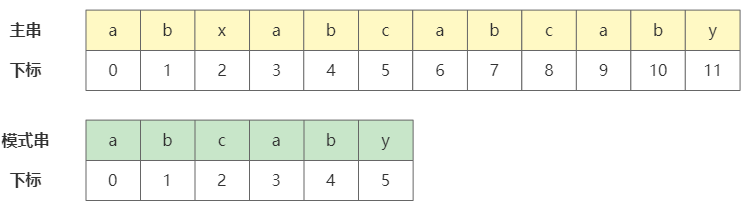
假设存在主串 abxabcabcaby、模式串 abcaby,我们需要判断两者是否相匹配,找到第一个字符在主串中出现的位置。当然我们裸眼求得话肯定可以看得出来两者是匹配的,且在主串下标为6时为第一个字符出现的位置。下面将对整个过程以KMP的思想进行演示:
一开始肯定是主串的第一个字符与模式串的第一个字符进行比较,最理想的情况就是从第一个字符开始就一路正确匹配直至结束。但显然在这里不是,在匹配到主串下标为2时发现 x和c 并不匹配。
如果按照暴力求解的方式,这种情况就会进行回溯,将模式串向后滑动一位,将主串下标为1的字符重新和模式串下标为0的字符匹配。但是按照KMP算法的思想,则是去掉了回溯,而是将模式串向右“滑动”尽可能远的一段距离后,继续进行比较。那么怎么体现呢?这里则是将模式串向后滑动至模式串下标为0与主串下标为2的 x 对齐,再继续进行比较。至于为什么模式串要这么移动,在后面的步骤再进行介绍。
这时主串与模式串对齐的字符并不匹配,但这是模式串已经无法移动了,因为模式串中与主串对齐的下标已经为零,那又怎么办呢?这时就会带动匹配框与模式串,使模式串与主串的下一个字符进行比较。
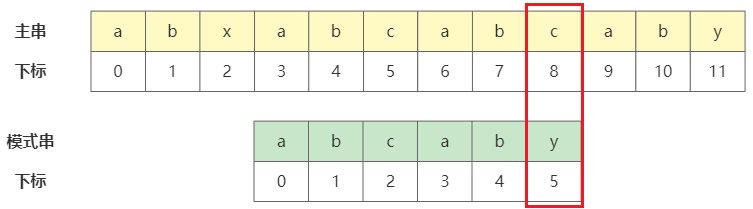
通过我们裸眼观察,发现接下来几乎是一马平川地匹配,直到主串下标为8与模式串下标为5的字符不匹配才停下。
真是可恶,就差这最后一步就成功了啊!难道这个时候又按照前面说的,将主串下标为8的字符重新与模式串下标为0的字符进行匹配吗?显然不是,如果进行该操作的话,很明显我们将会错过正确的结果。既然不是这样移动,那又该如何移动呢?这就是前面留下的疑问,如果决定模式串移动的方式。
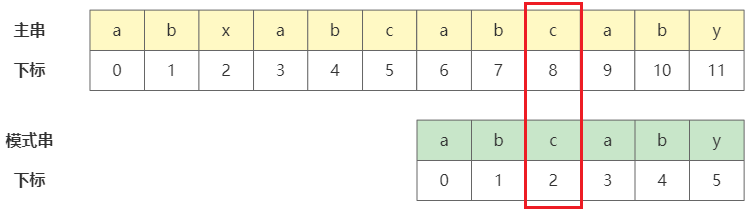
这里涉及到一个相同前后缀的情况。在上图中我们通过观察模式串,可以发现在下标为5之前即下标0-4的字符中,存在最长相同前后缀为 ab,那么我们是不是可以将模式串移动至前缀的 ab 与主串中后方的 ab 对齐就可以了呢?
是的,因为 ab 为此时模式串共同的前后缀,而主串中后方的 ab 已经和模式串中后缀匹配过了,直接将共同前缀的 ab 移动至与主串中后方的 ab 对齐的想法是可行的,这就相当于数学中的 因为a = b, b = c,所以a = c。当然如果没有相同的前后缀,就得乖乖滑动模式串至下标为0的位置重新比较了。
注意的是在移动模式串时,匹配框依旧停留在主串下标为8的位置上。
当继续往下匹配时,我们发现模式串能够成功地走完,全部与主串匹配上,这时主串也刚好走完。
2.2、寻找相同前后缀
通过上面串的匹配图解可能应该大概已经对匹配过程有了一个了解,但是又出现了一个问题,我们该怎么确定模式串中最长相同前后缀是否存在,具体又是什么呢?这里我们就需要引入KMP中恶名昭著的next数组了。在上面串的匹配中不知道大家有没有发现,在确定前后缀的时候,其实是只需要对着模式串寻找就可以了,并不需要主串,因此在下面的图解中也只会有模式串的出现。
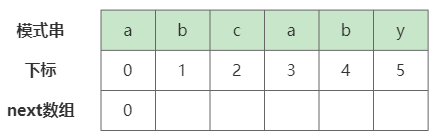
模式串第一个字符,即下标为0的字符对应next中的数值为0,这是因为其前面没有任何一个前缀与其对比。
这里简单介绍一下next数组的含义。当任意下标的模式串字符为后缀的最后一个字符时,next数组中存放的值为模式串与主串对齐的下标。如这里如果 a 为最后一个后缀,则会将 0 作为模式串与主串对齐的下标,因为a对应模式串下标index = 0,next[index] = 0。后续每一个步骤都将会简单介绍next数组的情况,应该对加深理解会有一定的帮助。
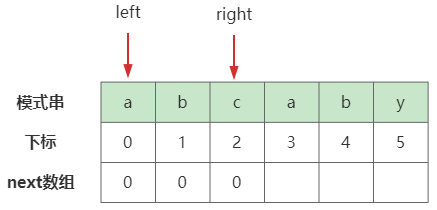
在后续的字符中,我们需要设置两个指针,与双指针的思想很类似。两个指针分别命名为 left 和 right,分别指向前缀与后缀,当然 right 也是用于遍历模式串的标识。但这里的 right 从1开始。我们将指针 right 逐步往后移,一直到下标为2都没有找到一个后缀能与前缀相同,因此这些的next数组中对应的元素都为0,当匹配框前面为这三个时都会以**下标为next[0]**的字符与主串对齐。
当继续往后移动时,会发现下标为3的字符与指针 left 指向的字符相同,相同时时候我们就可以将 right 指向的next数组元素设置为 left+1,意为当前字符(right指向,如下标为3的a)有相同前缀,且长度为1,如果当前是后缀的最后一个字符,可将下标为 next[3] = 1的字符与主串对齐。
接下来会将 left 和 right 两个指针都往后移,更新指针的指向。一直到y(下标为5)之前,都是这一类的情况,如 right 指向下标为4时,b与 left 指向的b相同,因此next数组元素为 next[4-1]+1 = 2。
因为上面的b和b相同,因为两个指针再次同步往后移,分别指向c和y,这时又不相同了又该怎么办呢?
这时我们会令 left = next[left],在这里就是 left = next[1] = 0。这里相当于正对于 left 指针前面的串进行了一次寻找相同前后缀的步骤,因此此时两个指针的指向如下:
这个时候就会和刚开始的情况相似了,指针 left 前面没有可指向的字符,且两个指针指向的字符不相同,因此这里指针 right 指向的next数组元素为 0,意为当匹配框前面最后一个字符为y(下标为5)时,会以**下标为next[0]**的字符与主串对齐。
以下就是我们最终的next数组啦,以指针 right 走完为结束标识,其中的元素即为与主串对齐的下标。
3、真枪实战
这里主要用力扣里面的题目力扣28. 找出字符串中第一个匹配项的下标训练KMP算法。
3.1、题目描述
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
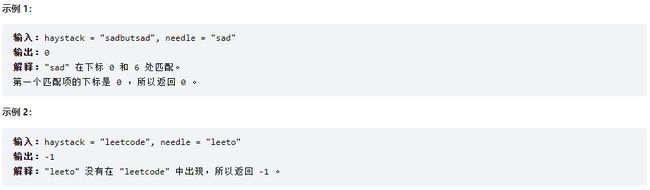
3.2、示例
3.3、提示
1 <= haystack.length, needle.length <= 104haystack和needle仅由小写英文字符组成
3.4、思路
这里的思路其实与前面的图解KMP思想完全一致,那么在这里就简单描述一下整个程序的流程吧。
- 获取next数组,并维护主串遍历下标属性和模式串遍历下标属性;
- 循环匹配串,当走完主串或者模式串时循环结束,即两者都不走完时循环继续
- 字符匹配,同时向前移动继续匹配下一对字符
- 字符不匹配,判断模式串遍历下标是否为零,为零时证明子串前没有需要判断的字符,主串向前移动,否则模式串移动至next数组指定位置
- 匹配结束,判断是否匹配成功,如果模式串已经走完则证明匹配完成,不可能存在最后一个不匹配模式串遍历下标还走完的,因为模式串的下标会
3.5、具体实现
/**
* @author xbaozi
* @version 1.0
* @classname SubstringSearch
* @date 2022-10-19 14:56
* @description 以力扣28. 找出字符串中第一个匹配项的下标训练KMP算法
*/
public class SubstringSearch {
/**
* 给你两个字符串haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。
* 如果needle 不是 haystack 的一部分,则返回 -1 。
*
* @param haystack 主串
* @param needle 模式串
* @return 第一个匹配项的下标,不匹配返回-1
*/
public int strStr(String haystack, String needle) {
return KMP(haystack, needle);
}
/**
* KMP算法实现
*
* @param text 主串
* @param pattern 需要匹配的模式串
* @return 第一个匹配项的下标,不匹配返回-1
*/
public int KMP(String text, String pattern) {
// 获取next数组
int[] next = computeTemporaryArray(pattern);
// 主串遍历下标
int textIndex = 0;
// 模式串遍历下标
int patternIndex = 0;
// 当走完主串或者模式串时循环结束,即两者都不走完时循环继续
while (textIndex != text.length() && patternIndex != pattern.length()) {
// 判断当前字符是否匹配
if (text.charAt(textIndex) == pattern.charAt(patternIndex)) {
// 字符匹配,同时向前移动继续匹配下一对字符
++textIndex;
++patternIndex;
} else {
// 字符不匹配,判断patternIndex是否为零
if (patternIndex > 0) {
// 不为零,模式串移动至next指定位置
patternIndex = next[patternIndex - 1];
} else {
// 为零,子串前没有需要判断的字符,主串向前移动
++textIndex;
}
}
}
// 匹配结束,判断是否匹配成功,如果模式串已经走完则证明匹配完成,不可能存在最后一个不匹配patternIndex还走完的,因为模式串的下标会向前移动
if (patternIndex == pattern.length()) {
// 两个串走的差值刚好是第一个匹配的下标
return textIndex - patternIndex;
}
return -1;
}
/**
* 根据模式串计算临时数组,该临时数组为KMP算法中的next数组
*
* @param pattern 模式串
* @return 返回计算出来的临时数组next
*/
public int[] computeTemporaryArray(String pattern) {
int[] next = new int[pattern.length()];
// 左指针,指向前缀
int left = 0;
// 右指针一直向前,指向后缀,同时也是next数组遍历的循环下标,从1开始
int right = 1;
while (right < pattern.length()) {
// 判断前后缀是否匹配
if (pattern.charAt(left) == pattern.charAt(right)) {
// 如果匹配,则next数组right下标的元素在left的基础上+1
next[right] = left + 1;
// 左右指针都需要往前移
++left;
++right;
} else {
// 如果不匹配,判断left是否为零,避免下标溢出
if (left > 0) {
// left下标值换成left-1所指向的值
left = next[left - 1];
} else {
// left等于零,next数组当前指向元素需要置零,证明当前没有任何匹配的前后缀,右指针需要继续往前走寻找与前缀匹配的后缀
next[right++] = 0;
}
}
}
return next;
}
}
3.6、测试结果
分别编写next数组获取与匹配结果的测试方法,运行之后会发现答案是我们想要的。
public class SubstringSearchTest {
@Test
public void testComputeTemporaryArray() {
int[] next = new SubstringSearch().computeTemporaryArray("abcaby");
System.out.println("得到的next数组为:" + Arrays.toString(next));
}
@Test
public void testKMP() {
int kmpIndex = new SubstringSearch().KMP("abxabcabcaby","abcaby");
System.out.println("第一次匹配的下标为:" + kmpIndex);
}
}
最后贴上力扣运行结果: