模拟,风险和度量 (SIMULATIONS, RISKS, AND METRICS)
Note from Towards Data Science’s editors: While we allow independent authors to publish articles in accordance with our rules and guidelines, we do not endorse each author’s contribution. You should not rely on an author’s works without seeking professional advice. See our Reader Terms for details.
Towards Data Science编辑的注意事项: 尽管我们允许独立作者按照我们的 规则和指南 发表文章 ,但我们不认可每位作者的贡献。 您不应在未征求专业意见的情况下依赖作者的作品。 有关 详细信息, 请参见我们的 阅读器条款 。
Let’s disassemble backtests and make them great again :) In the previous part, we have reviewed the main dangers of the classic backtesting routine with the historical data and standard metrics related to the strategy performance. We have introduced new statistics groups related to data, models, efficiency, and trades that can present more insights about the underlying strategy.
让我们分解回溯测试,使其再次变得更好:)在上一部分中 ,我们使用与策略绩效相关的历史数据和标准指标,回顾了经典回溯例程的主要危险。 我们引入了与数据,模型,效率和交易相关的新统计组,可以提供有关基础策略的更多见解。
https://harrypotter.fandom.com/wiki/Doubling_Charm, no copyright infringement is intended https://harrypotter.fandom.com/wiki/Doubling_Charm ,无意侵犯版权However, as was mentioned, backtesting on a single historical path that was generated by some extremely complex stochastic process with numerous variables doesn’t seem adequate at all. It allows neither probabilistic interpretation, neither a scenario-based view on the strategy. This, second part of the article is about techniques that open to us a broader approach to validation of our quantitative strategies:
但是,正如前面提到的,对由具有多个变量的极其复杂的随机过程所产生的单一历史路径进行回测似乎根本不够。 它既不允许概率解释,也不允许基于策略的基于场景的视图。 本文的第二部分介绍了一些技术,这些技术为我们提供了更广泛的方法来验证我们的定量策略:
Backtesting through cross-validation: first, we will start a technique that will allow sampling stochastic data without knowing an explicit data generation model using cross-validation;
通过交叉验证进行回测:首先,我们将开始一项技术,该技术将允许在不知道使用交叉验证的显式数据生成模型的情况下对随机数据进行采样。
Backtesting on synthetic data: then, we will show how to use stochastic modeling and generation of sample paths for backtesting;
对合成数据进行回测:然后,我们将展示如何使用随机建模和样本路径生成进行回测;
Stress-scenario-based backtesting: lastly, we will check how to sample synthetic data with controlling the main factors, hence, allowing us to model exceptional situations.
基于压力场景的回测:最后,我们将检查如何在控制主要因素的情况下对合成数据进行采样,从而使我们能够对异常情况进行建模。
Like most of my recent articles, this one is inspired by books of Dr. Lopez De Prado and I recommend them to dive deeper into the topic. As always, the source could you can find on my GitHub.
像我最近的大多数文章一样,该文章的灵感来自洛佩兹·德普拉多(Lopez De Prado)博士的书,我建议他们更深入地研究该主题。 与往常一样,您可以在我的GitHub上找到源。
通过交叉验证进行回测 (Backtesting through cross-validation)
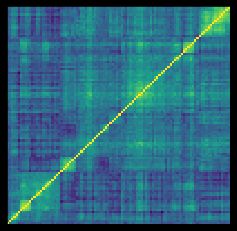
Long story short, we want to have more than one historical path to check our strategy performance. We could sample it somehow from the historical data, but in what way? We could take different parts from different times from the whole dataset as training and testing sets. For generating these parts we already know the mechanism — it’s called cross-validation. For our purposes, we need as rich as possible a set of simulations — all possible combinations of subsets for training and testing the algorithm, which brings us the Combinatorial Purged Cross-Validation algorithm:
长话短说,我们希望有一条历史之路来检验我们的战略绩效。 我们可以从历史数据中以某种方式对其进行采样 ,但是用什么方式呢? 我们可以将整个数据集中来自不同时间的不同部分作为训练和测试集。 为了生成这些部分,我们已经知道了这种机制-称为交叉验证 。 为了我们的目的,我们需要尽可能丰富的一组模拟-训练和测试该算法的子集的所有可能组合 ,这为我们带来了组合清除交叉验证算法:
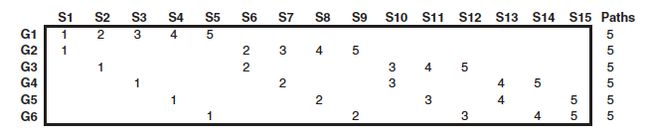
https://www.amazon.com/Advances-Financial-Machine-Learning-Marcos/dp/1119482089 and https://www.amazon.com/Advances-Financial-Machine-Learning-Marcos/dp/1119482089和 http://www.quantresearch.org/Innovations.htm http://www.quantresearch.org/Innovations.htmFor example, we split the whole dataset into N = 6 groups G1…G6, from which we take 2 for testing purposes randomly. Hence, we can have options of 15 splits shown above as columns S1…S15. In each of these splits, 2 groups are for testing and 4 groups are for training with all combinations present. Now, we can test our algorithm 15 times more than with a single backtest and obtaining the distribution of related Sharpe ratios and other risk measures. Despite all the advantages, this method has some drawbacks:
例如,我们将整个数据集分为N = 6组G1…G6 ,从中我们随机抽取2个用于测试目的。 因此,我们可以有15个拆分的选项,如列S1…S15所示 。 在所有这些分组中,有2组用于测试,4组用于训练并使用所有存在的组合。 现在, 我们可以比单次回测多测试15次算法 ,并获得相关的Sharpe比率和其他风险度量的分布 。 尽管具有所有优点,但此方法有一些缺点:
it doesn’t allow historical interpretation,
它不允许历史解释 ,
data leakages are possible and it needs to be fixed separately.
数据可能泄漏 ,需要单独修复。
对综合数据进行回测 (Backtesting on synthetic data)
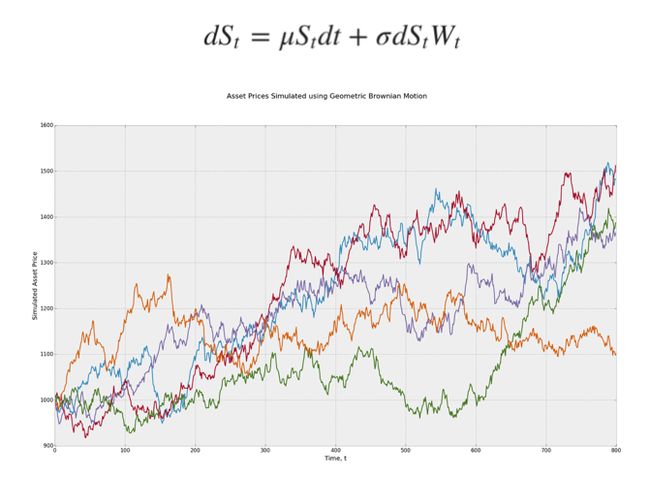
Combinatorial Purged Cross-Validation is a powerful tool, but it limits us to the subsets of the data available. In financial mathematics, we are using Monte-Carlo simulations for thousands and millions of times to get accurate estimates. For example, in derivatives pricing, we use stochastic differential equations to simulate underlying prices, and depending on the equation, these stochastic simulations can look very different:
组合清除交叉验证是一个功能强大的工具,但将我们限制为可用数据的子集。 在金融数学中,我们使用了成千上万次的蒙特卡洛模拟来获得准确的估计。 例如,在衍生产品定价中,我们使用随机微分方程式来模拟基础价格,并且根据方程式,这些随机模拟可能看起来非常不同:
Such simulations can give us many different backtest data, but we have two problems here: we don’t know from which exactly stochastic process financial data is sampled from, and how to re-create exogenous variables as fundamentals, sentiment, etc.
这样的模拟可以为我们提供许多不同的回测数据,但是这里存在两个问题:我们不知道从哪个随机过程财务数据中准确采样,以及如何重新创建作为基本面,情绪等的外生变量 。
The first problem can be solved via the calibration process, i.e. finding exact values of parameters as drift, volatility, jump probability, mean-reversion coefficient, etc.
第一个问题可以通过校准过程解决,即找到诸如漂移,波动率,跳跃概率,均值回复系数等参数的精确值。
The second one is more sophisticated. In the code I used for the experiments, I am training a separate machine learning model to predict high, low, open prices and volume using the close price only. Seems like overkill (and overfit), but we don’t aim to predict anything here, just to replicate underlying dynamics, hence, it’s more or less legit (but doubtful, if you know better approaches — let me know please).
第二个更复杂。 在用于实验的代码中 ,我正在训练一个单独的机器学习模型,以仅使用收盘价来预测高,低,开盘价和交易量。 看起来像是过度杀伤(和过度拟合),但我们不打算在这里预测任何东西,仅仅是为了复制潜在的动态,因此,它或多或少是合法的(但值得怀疑,如果您知道更好的方法,请告诉我)。
The end result is a distribution of backtest metrics over different scenarios, the same as with the combinatorial cross-validation approach.
最终结果是回测指标在不同情况下的分布,与组合交叉验证方法相同。
压力情景回测 (Stress scenario backtesting)
Simulations can be used also for the generation of specific regimes and scenarios we’re interested in. For example, we are interested in knowing how our strategy will behave in cases of sudden market falls. How we could do it? If we take just historical data, we can find 2–3 of such crises depending on the market. Here, Monte-Carlo simulations are useful again, but we need to pick the parameters of the particular stochastic process very carefully: to model the exact risk that we are testing this strategy against. For example, for market falls described above, we can simulate the jump-diffusion process with a negative jump size and corresponding frequency.
模拟还可以用于生成我们感兴趣的特定机制和场景。例如,我们有兴趣了解在市场突然下跌的情况下我们的策略将如何表现。 我们该怎么做? 如果仅采用历史数据,则取决于市场,我们会发现2-3种此类危机。 在这里,蒙特卡洛模拟再次很有用,但是我们需要非常仔细地选择特定随机过程的参数:为测试该策略所针对的确切风险建模。 例如,对于上述市场下跌,我们可以模拟具有负跳数和相应频率的跳扩散过程。
There are also other data-driven ways to simulate realistic scenarios based on the generative machine learning models as GANs. There are several promising approaches for both returns time series generation and correlation matrices sampling:
还有其他数据驱动的方法,可以基于生成的机器学习模型(如GAN)来模拟现实情况。 对于返回时间序列生成和相关矩阵采样,有几种有希望的方法:
However, usually, GANs don’t allow us controlled scenario generation, since neural representations are entangled, i.e. we can’t tell where is the “button” for manipulating drift, volatility, or another financial variable. Variational autoencoders could be an interesting approach here, I wrote an article on disentangled representation learning a while ago which might be useful here.
但是,通常,GAN 不允许我们生成受控的情景 ,因为神经表示会纠缠在一起,即我们无法分辨操纵漂移,波动率或其他金融变量的“按钮”在哪里。 变体自动编码器在这里可能是一种有趣的方法,我写了一篇有关解缠表示的文章,前一阵子在这里可能很有用。
A brief illustration of beta-VAEs trying to disentangle different market properties from raw data. More details at https://towardsdatascience.com/gans-vs-odes-the-end-of-mathematical-modeling-ec158f04acb9 beta-VAE试图从原始数据中区分不同市场属性的简要说明。 有关更多详细信息, 请访问 https://towardsdatascience.com/gans-vs-odes-the-end-of-mathematical-modeling-ec158f04acb9数值实验 (Numerical experiments)
Let’s take Deutsche Bank stock price data as we did in the previous article. The backtests of the ML-based strategy looked very well until we realized that on other banks this approach fails, which doesn’t allow us to consider our financial finding credible. Now, I would like to show, how we could realize it without looking at similar market players, but using probabilistic interpretations of the metrics.
让我们像上一篇文章那样获取德意志银行的股价数据。 在我们意识到在其他银行这种方法失败之前,基于ML的策略的回测看起来非常好,这使我们无法认为我们的财务发现可信。 现在,我想展示一下,如何在不考虑类似市场参与者的情况下如何使用指标的概率解释来实现它。
组合交叉验证 (Combinatorial cross-validation)
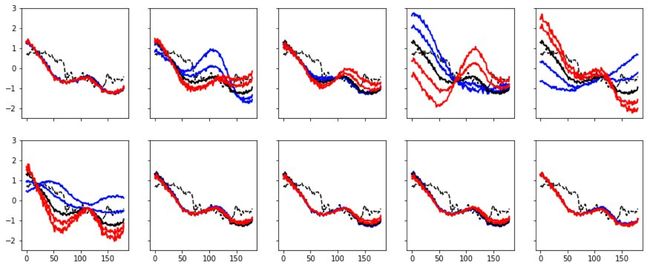
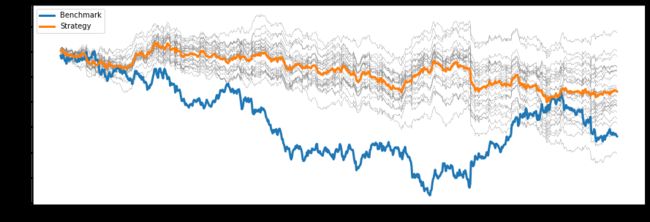
Let’s reshuffle the first pieces of our price time series to generate 15 train and backtests paths (as we discussed above). We can see on some of the illustrations below, how our backtest data already has different market regimes and directions which immediately allows scenario-based validation:
让我们重新调整价格时间序列的前几部分,以生成15条训练和回测路径(如上所述)。 我们可以在下面的一些插图中看到,我们的回测数据如何已经具有不同的市场制度和方向,从而可以立即进行基于场景的验证:
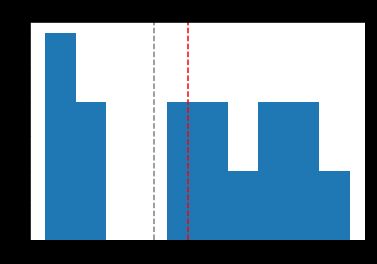
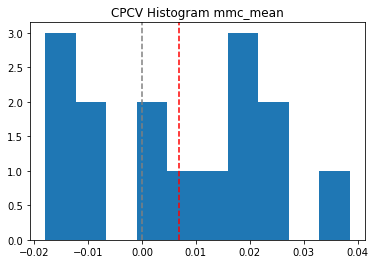
After we run the ML and strategy pipeline from the previous post, we should check the performances of ML models first on these backtest data, and only after we will be confident in machine learning performance, we can run strategy backtests. From the histogram below, we can see, that on average MCC (Matthews Correlation Coefficient) is positive, however, there are several data pieces that give us negative performance (we already can estimate some risks from here).
在运行上一篇文章中的ML和策略管道之后 ,我们应该首先在这些回测数据上检查ML模型的性能,只有在对机器学习性能充满信心之后,我们才能运行策略回测。 从下面的直方图中,我们可以看到,平均MCC(马修斯相关系数)为正,但是,有几个数据片段给我们带来了负面的表现(我们已经可以从此处估算一些风险)。
Let’s assume the risk is acceptable and plot histograms for strategy Sharpe ratio, Deflated Sharpe ratio, and Probabilistic Sharpe ratio (see the previous article for more details). We can see a “fatter” left tail in the Sharpe ratios compared to the MCCs histogram, and, more important, the total prevalence of zero-valued Deflated Sharpe ratios on these backtests, which means, that our results are prone to the issue of the repeated experiments and are not reliable.
让我们假设风险是可以接受的,并绘制策略夏普比率,放气夏普比率和概率夏普比率的直方图(有关更多详细信息,请参见上一篇文章 )。 与“我的客户中心”直方图相比,我们可以看到Sharpe比率中有一个“较轻”的左尾巴 ,更重要的是,在这些回溯测试中零值化Deflate Sharpe比率的总患病率,这意味着我们的结果容易出现重复的实验并不可靠。
As we can see, a single walk-forward couldn’t open to us these problems, and simple combinatorial cross-validation already shows much more compared to the point metrics estimate.
正如我们所看到的,单步前进无法解决这些问题,与点度量估计相比,简单的组合交叉验证已显示出更多的优势。
蒙特卡洛模拟 (Monte-Carlo simulations)
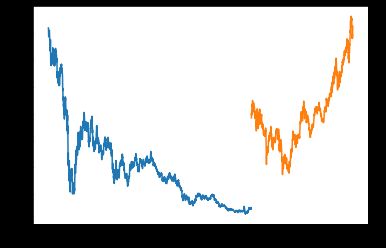
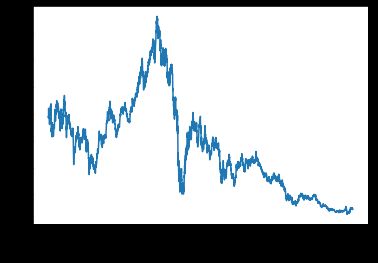
If combinatorial cross-validation works so well, what can we do with the simulations from the stochastic models? Let’s look at the DB prices time series below, how it behaves? What stochastic model and what parameters are describing it?
如果组合交叉验证效果很好,那么我们如何处理随机模型的仿真呢? 让我们看看下面的DB价格时间序列,它的表现如何? 什么随机模型和什么参数来描述它?
We can clearly see some jumps (and time-varying volatility too by the way), but for simplicity, let’s assume that this process follows the Merton jump-diffusion model, with drift and volatility taken from the historical data (-3.036e-05, 0.02789), jump intensity, size, and its standard deviation chosen “on the eye” (0.1, -0.01, 0.001). Let’s simulate a couple of paths of such close price time series, predict corresponding low, high, open prices, and the volume and backtest strategies on these generated paths.
我们可以清楚地看到一些跳跃(顺便说一下,波动率也随时间变化),但是为简单起见,我们假设此过程遵循Merton跳跃扩散模型 ,其中漂移和波动率取自历史数据(-3.036e-05 (0.02789),跳跃强度,大小及其标准偏差选择为“在眼睛上”(0.1,-0.01、0.001)。 让我们模拟几个这样的接近价格时间序列的路径,预测相应的低价,高价,开盘价以及这些生成的路径上的数量和回测策略。
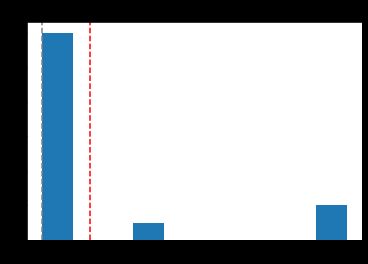
From the first one, we can see from the distribution of MCCs calculated over multiple runs of the bagging classifier, that on average our model accuracy out-of-sample is negative. It should’ve stopped us from running the backtest, but out of curiosity let’s do this and we can see, that such a backtest can be lying — it outperforms the benchmark even with a poor model! A good point to the previous article on the importance of the correct metrics calculation and tracking.
从第一个中可以看出,从在多次套袋分类器中计算出的MCC分布来看,平均而言,样本外模型的精度为负 。 它本应阻止我们进行回溯测试,但是出于好奇,让我们执行此操作,我们可以看到,这样的回溯测试可能存在谎言,即使在模型较差的情况下也能跑赢基准测试! 关于上一篇文章的正确点是正确计算和跟踪的重要性。
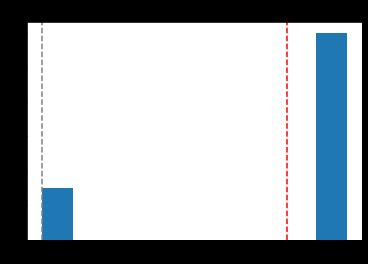
Re-launching simulation gives similar bearish time series, but now with more jumps over time (which looks more similar to the original DB time series), but the distribution of MCCs gives negative results again, and the backtest is again misleading.
重新启动模拟给出了相似的看跌时间序列,但是现在随着时间的推移出现了更多跳跃(这看起来更类似于原始的DB时间序列),但是MCC的分布再次给出了负结果 ,并且回测再次引起了误导。
Of course, if we will re-sample this time series more times and will build a histogram of such predictions, we will clearly see a fat left tail in model accuracies which will clearly signal to us that our initial financial hypothesis doesn’t hold anymore if we sample data with very similar dynamics, yet a bit different from the historical data. Which shouldn’t be the case if we did our preliminary research right :)
当然,如果我们将更多时间对该时间序列进行重新采样并建立此类预测的直方图,则我们将清楚地看到模型精度中的粗尾巴,这显然向我们表明我们的初始财务假设不再成立如果我们以非常相似的动力学采样数据,但与历史数据有些不同。 如果我们进行了初步研究,那就不应该这样了:)
结论 (Conclusions)
In this article, we have reviewed techniques that allow probabilistic backtest as compared to the historical walk-forward ones. The main problem of the latter is that it is just a single realization of a complex stochastic process that could have gone in many different ways, and we don’t want to overfit to one sample from a distribution.
在本文中,我们回顾了与历史遍历相比允许概率回测的技术。 后者的主要问题在于,它只是一个复杂随机过程的单一实现,而该过程可能已经以许多不同的方式进行了,并且我们不想过度拟合分布中的一个样本 。
We have used two major techniques to address this problem: combinatorial cross-validation and stochastic simulations, each with its benefits and drawbacks. In the previous article, we have seen that our ML-based strategy performed well on the DB stock price, but experiments on the other assets from the banking universe have shown, that this “finding” doesn’t generalize to the market. In this article, we have shown, that if we used not walk-forward estimates, but combinatorial CV or stochastic simulations, we could see that this strategy is not reliable even without checking other assets on the market, which could save us time for the research.
我们使用了两种主要技术来解决此问题: 组合交叉验证和随机模拟 ,每种都有其优点和缺点。 在上一篇文章中 ,我们已经看到我们基于ML的策略在DB股票价格上表现良好,但是对银行业其他资产的实验表明,这种“发现”并不能推广到市场。 在本文中,我们已经表明,如果不使用前瞻性估计,而是使用组合CV或随机模拟,则即使不检查市场上的其他资产,我们也可以看到该策略是不可靠的,这可以为我们节省时间。研究。
We have studied additional metrics that tell more us about backtest performance and we have expanded them to the probabilistic estimates. We do this all to estimate the risk of our strategy performing poorly out-of-sample, which is relevant to measuring the “overfitting” of these strategies. We also know, that overfitting is about the tradeoff between in-sample and out-of-sample performance, and in these two articles, we were focused only on the OOS one. In the next, third article in this short series, we will focus on other measures of overfitting risk that takes into account in-sample data as well and will conclude with a general framework for testing quantitative trading strategies. Stay tuned and don’t forget to check out the source code :)
我们研究了其他指标,这些指标可以使我们更多地了解回测性能,并将其扩展到概率估计。 我们通过所有这些操作来估计我们的策略执行样本不足的风险,这与衡量这些策略的“过拟合”有关 。 我们也知道,过度拟合是关于样本内和样本外性能之间的权衡,在这两篇文章中,我们仅关注于OOS。 在这个简短系列的下一篇文章的第三篇中,我们将着重于考虑样本数据的其他过度拟合风险的度量,并以测试量化交易策略的通用框架作为结束。 请继续关注,不要忘记查看源代码 :)
P.S.You also can connect with me on the Facebook blog or Linkedin, where I regularly post some AI articles or news that are too short for Medium and Instagram for some more personal content :)
PS您还可以在Facebook博客或Linkedin上与我联系,我经常在其中发布一些AI文章或新闻,这些文章或新闻对于Medium和Instagram来说太短了,无法提供更多个人内容:)
翻译自: https://towardsdatascience.com/ai-in-finance-how-to-finally-start-to-believe-your-backtests-2-3-adfd13da20ec