keras之父《python深度学习》笔记 第八章

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

我们之前做的东西，都是被动性（目标识别）或者反应性（自动驾驶）任务，其实神经网络还能做创造性的任务，就是利用神经网络去输出文化生活内容。很大一部分艺术创作，从深度学习的角度来看都是简单的模式识别与专业技能。我们感知到的信息，语言和艺术作品，都是有统计结构的，而对统计结构的学习正是深度学习所擅长的。深度学习可以对会话音乐或者文学作品的潜在空间进行学习，然后从空间中采样，创造出与训练作品具有相似风格的新作品。虽然神经网络没有人类生活的经历，也没有人类情感。但是他们从数学运算的角度，去归纳统计艺术作品的特点。最后的结果还是人类来欣赏，用人类的感官来赋予意义。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、使用LSTM 生成文本

1.生成式网络的历史

LSTM算法在1997年已经开发出来了，但是知道2016年才开始用于生成序列数据。2002年曾经有人用LSTM来生成音乐，但是直到2016年，他才开始深入研究。差不多相同的时间Alex Graves
利用笔触位置的时间序列将循环混合密度网络应用于生成类似人类的手写笔迹，从那以后，循环神经网络被成功用于音乐生成、对话生成、图像生成、语音合成和分子设计，甚至有人用来生成小说、电视剧剧本。

2.如何生成序列数据

用深度学习生成序列数据的通用方法，就是使用前面的标记作为输入，训练一个网络（通
常是循环神经网络或卷积神经网络）来预测序列中接下来的一个或多个标记。例如，给定输入
the cat is on the ma，训练网络来预测目标t，即下一个字符。与前面处理文本数据时一样，标记
（token）通常是单词或字符，给定前面的标记，能够对下一个标记的概率进行建模的任何网络
都叫作语言模型（language model）。语言模型能够捕捉到语言的潜在空间（latent space），即语言的统计结构。
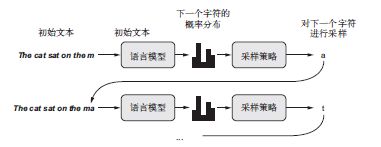
一旦训练好了这样一个语言模型，就可以从中采样（sample，即生成新序列）。向模型中输
入一个初始文本字符串［即条件数据（conditioning data）］，要求模型生成下一个字符或下一个
单词（甚至可以同时生成多个标记），然后将生成的输出添加到输入数据中，并多次重复这一过
程（见图8-1）。这个循环可以生成任意长度的序列，这些序列反映了模型训练数据的结构，它
们与人类书写的句子几乎相同。在本节的示例中，我们将会用到一个LSTM 层，向其输入从文
本语料中提取的N 个字符组成的字符串，然后训练模型来生成第N+1 个字符。模型的输出是对
所有可能的字符做softmax，得到下一个字符的概率分布。这个LSTM 叫作字符级的神经语言模
型（character-level neural language model）。

3.采样策略的重要性

生成文本的时候，选择下一个字符有两种方式。最简单直接的是贪婪采样，就是始终选择可能性最大的下一个字符。但是这种方法会得到重复的、可预测的字符串，看起来不像是人类语言。另一种实践中采用较多的是随机采样：比如根据模型结果，如果下一个字符预测为e的概率为0.3，那么就有30%的可能选择它。其实广义上来讲贪婪采样也算是一种随机采样，只不过某个字符的概率为1。

为什么需要有一定的随机性？考虑一个极端的例子——纯随机采样，即从均匀概率分布中
抽取下一个字符，其中每个字符的概率相同。这种方案具有最大的随机性，换句话说，这种概
率分布具有最大的熵。当然，它不会生成任何有趣的内容。再来看另一个极端——贪婪采样。
贪婪采样也不会生成任何有趣的内容，它没有任何随机性，即相应的概率分布具有最小的熵。
从“真实”概率分布（即模型softmax 函数输出的分布）中进行采样，是这两个极端之间的一
个中间点。但是，还有许多其他中间点具有更大或更小的熵，你可能希望都研究一下。更小的
熵可以让生成的序列具有更加可预测的结构（因此可能看起来更真实），而更大的熵会得到更加
出人意料且更有创造性的序列。从生成式模型中进行采样时，在生成过程中探索不同的随机性
大小总是好的做法。我们人类是生成数据是否有趣的最终判断者，所以有趣是非常主观的，我
们无法提前知道最佳熵的位置。
为了在采样过程中控制随机性的大小，我们引入一个叫作softmax 温度（softmax temperature）
的参数，用于表示采样概率分布的熵，即表示所选择的下一个字符会有多么出人意料或多么可
预测。给定一个temperature 值，将按照下列方法对原始概率分布（即模型的softmax 输出）进行重新加权，计算得到一个新的概率分布。

import numpy as np
def reweight_distribution(original_distribution, temperature=0.5):
distribution = np.log(original_distribution) / temperature
distribution = np.exp(distribution)
return distribution / np.sum(distribution)

更高的温度得到的是熵更大的采样分布，会生成更加出人意料、更加无结构的生成数据，
而更低的温度对应更小的随机性，以及更加可预测的生成数据

4.字符级LSTM文本生成实现

下面用Keras 来实现这些想法。首先需要可用于学习语言模型的大量文本数据。我们可以
使用任意足够大的一个或多个文本文件——维基百科、《指环王》等。本例将使用尼采的一些作
品，他是19 世纪末期的德国哲学家，这些作品已经被翻译成英文。因此，我们要学习的语言模
型将是针对于尼采的写作风格和主题的模型，而不是关于英语的通用模型。

import keras
import numpy as np
path = keras.utils.get_file(
'nietzsche.txt',
origin='https://s3.amazonaws.com/text-datasets/nietzsche.txt')
text = open(path).read().lower()
print('Corpus length:', len(text))

接下来，我们要提取长度为maxlen 的序列（这些序列之间存在部分重叠），对它们进行
one-hot 编码，然后将其打包成形状为(sequences, maxlen, unique_characters) 的三维
Numpy 数组。与此同时，我们还需要准备一个数组y，其中包含对应的目标，即在每一个所提
取的序列之后出现的字符（已进行one-hot 编码）。

maxlen = 60
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
print('Number of sequences:', len(sentences))
chars = sorted(list(set(text)))
print('Unique characters:', len(chars))
char_indices = dict((char, chars.index(char)) for char in chars)
print('Vectorization...')
x = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
x[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
from keras import layers
model = keras.models.Sequential()
model.add(layers.LSTM(128, input_shape=(maxlen, len(chars))))
model.add(layers.Dense(len(chars), activation='softmax'))

optimizer = keras.optimizers.RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)

给定一个训练好的模型和一个种子文本片段，我们可以通过重复以下操作来生成新的文本。
(1) 给定目前已生成的文本，从模型中得到下一个字符的概率分布。
(2) 根据某个温度对分布进行重新加权。
(3) 根据重新加权后的分布对下一个字符进行随机采样。
(4) 将新字符添加到文本末尾。
下列代码将对模型得到的原始概率分布进行重新加权，并从中抽取一个字符索引［采样函
数（sampling function）

def sample(preds, temperature=1.0):
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / temperature
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)

最后，下面这个循环将反复训练并生成文本。在每轮过后都使用一系列不同的温度值来生成
文本。这样我们可以看到，随着模型收敛，生成的文本如何变化，以及温度对采样策略的影响。

import random
import sys
for epoch in range(1, 60):
print('epoch', epoch)
model.fit(x, y, batch_size=128, epochs=1)
start_index = random.randint(0, len(text) - maxlen - 1)
generated_text = text[start_index: start_index + maxlen]
print('--- Generating with seed: "' + generated_text + '"')
for temperature in [0.2, 0.5, 1.0, 1.2]:
print('------ temperature:', temperature)
sys.stdout.write(generated_text)
for i in range(400):
sampled = np.zeros((1, maxlen, len(chars)))
for t, char in enumerate(generated_text):
sampled[0, t, char_indices[char]] = 1.
preds = model.predict(sampled, verbose=0)[0]
next_index = sample(preds, temperature)
next_char = chars[next_index]
generated_text += next_char
generated_text = generated_text[1:]
sys.stdout.write(next_char)

这里我们使用的随机种子文本是new faculty, and the jubilation reached its climax when kant。
第20 轮时，temperature=0.2 的输出如下所示，此时模型还远没有完全收敛。

new faculty, and the jubilation reached its climax when kant and such a man in the
same time the spirit of the surely and the such the such
as a man is the sunligh and subject the present to the superiority of the special
pain the most man and strange the subjection of the
special conscience the special and nature and such men the subjection of the
special men, the most surely the subjection of the special
intellect of the subjection of the same things and
temperature=0.5 的结果如下所示。
new faculty, and the jubilation reached its climax when kant in the eterned and such
man as it’s also become himself the condition of the
experience of off the basis the superiory and the special morty of the strength, in
the langus, as which the same time life and "even who
discless the mankind, with a subject and fact all you have to be the stand
and lave no comes a troveration of the man and surely the
conscience the superiority, and when one must be w
temperature=1.0 的结果如下所示。
new faculty, and the jubilation reached its climax when kant, as a
periliting of manner to all definites and transpects it it so
hicable and ont him artiar resull
too such as if ever the proping to makes as cnecience. to been juden,
all every could coldiciousnike hother aw passife, the plies like
which might thiod was account, indifferent germin, that everythery
certain destrution, intellect into the deteriorablen origin of moralian,
and a lessority o

第60 轮时，模型已几乎完全收敛，文本看起来更加连贯。此时temperature=0.2 的结果
如下所示。
cheerfulness, friendliness and kindness of a heart are the sense of the
spirit is a man with the sense of the sense of the world of the
self-end and self-concerning the subjection of the strengthorixes–the
subjection of the subjection of the subjection of the
self-concerning the feelings in the superiority in the subjection of the
subjection of the spirit isn’t to be a man of the sense of the
subjection and said to the strength of the sense of the
temperature=0.5 的结果如下所示。
cheerfulness, friendliness and kindness of a heart are the part of the soul
who have been the art of the philosophers, and which the one
won’t say, which is it the higher the and with religion of the frences.
the life of the spirit among the most continuess of the
strengther of the sense the conscience of men of precisely before enough
presumption, and can mankind, and something the conceptions, the
subjection of the sense and suffering and the
temperature=1.0 的结果如下所示。
cheerfulness, friendliness and kindness of a heart are spiritual by the
ciuture for the
entalled is, he astraged, or errors to our you idstood–and it needs,
to think by spars to whole the amvives of the newoatly, prefectly
raals! it was
name, for example but voludd atu-especity"–or rank onee, or even all
"solett increessic of the world and
implussional tragedy experience, transf, or insiderar,–must hast
if desires of the strubction is be stronges

可见，较小的温度值会得到极端重复和可预测的文本，但局部结构是非常真实的，特别是
所有单词都是真正的英文单词（单词就是字符的局部模式）。随着温度值越来越大，生成的文本
也变得更有趣、更出人意料，甚至更有创造性，它有时会创造出全新的单词，听起来有几分可信（比
如eterned 和troveration）。对于较大的温度值，局部模式开始分解，大部分单词看起来像是半随
机的字符串。毫无疑问，在这个特定的设置下，0.5 的温度值生成的文本最为有趣。一定要尝试
多种采样策略！在学到的结构与随机性之间，巧妙的平衡能够让生成的序列非常有趣。
注意，利用更多的数据训练一个更大的模型，并且训练时间更长，生成的样本会比上面的
结果看起来更连贯、更真实。但是，不要期待能够生成任何有意义的文本，除非是很偶然的情况。
你所做的只是从一个统计模型中对数据进行采样，这个模型是关于字符先后顺序的模型。语言
是一种信息沟通渠道，信息的内容与信息编码的统计结构是有区别的。为了展示这种区别，我
们来看一个思想实验：如果人类语言能够更好地压缩通信，就像计算机对大部分数字通信所做
的那样，那么会发生什么？语言仍然很有意义，但不会具有任何内在的统计结构，所以不可能
像刚才那样学习一个语言模型。

二、DeepDream

1.DeepDream介绍

DeepDream 是一种艺术性的图像修改技术，它用到了卷积神经网络学到的表示。DeepDream
由Google 于2015 年夏天首次发布，使用Caffe 深度学习库编写实现（当时比TensorFlow 的首
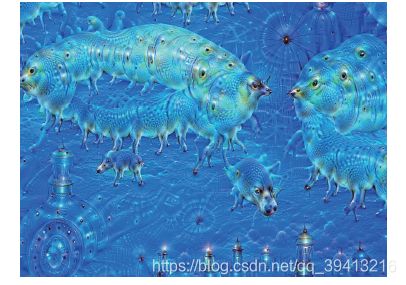
次公开发布要早几个月）。 它很快在网上引起了轰动，这要归功于它所生成的迷幻图像（比如
图8-3），图像中充满了算法生成的错觉式伪影、鸟羽毛和狗眼睛。这是DeepDream 卷积神经网
络在ImageNet 上训练的副作用，因为ImageNet 中狗和鸟的样本特别多。

DeepDream 算法与第卷积神经网络过滤器可视化技术几乎相同，都是反向运行
一个卷积神经网络：对卷积神经网络的输入做梯度上升，以便将卷积神经网络靠顶部的某一层
的某个过滤器激活最大化。DeepDream 使用了相同的想法，但有以下这几个简单的区别。

使用 DeepDream，我们尝试将所有层的激活最大化，而不是将某一层的激活最大化，因
此需要同时将大量特征的可视化混合在一起。
‰ 不是从空白的、略微带有噪声的输入开始，而是从现有的图像开始，因此所产生的效果
能够抓住已经存在的视觉模式，并以某种艺术性的方式将图像元素扭曲。
‰ 输入图像是在不同的尺度上［叫作八度（octave）］进行处理的，这可以提高可视化的质量。
我们来生成一些DeepDream 图像。

2.用Keras 实现DeepDream

我们将从一个在ImageNet 上预训练的卷积神经网络开始。Keras 中有许多这样的卷积神经
网络：VGG16、VGG19、Xception、ResNet50 等。我们可以用其中任何一个来实现DeepDream，
但我们选择的卷积神经网络会影响可视化的效果，因为不同的卷积神经网络架构会学到不同的
特征。最初发布的DeepDream 中使用的卷积神经网络是一个Inception 模型，在实践中，人们已
经知道Inception 能够生成漂亮的DeepDream 图像，所以我们将使用Keras 内置的Inception V3
模型。

from keras.applications import inception_v3
from keras import backend as K
K.set_learning_phase(0)
model = inception_v3.InceptionV3(weights='imagenet',
include_top=False)

接下来，我们要计算损失（loss），即在梯度上升过程中需要最大化的量。在第5 章的过滤
器可视化中，我们试图将某一层的某个过滤器的值最大化。这里，我们要将多个层的所有过滤
器的激活同时最大化。具体来说，就是对一组靠近顶部的层激活的L2 范数进行加权求和，然
后将其最大化。选择哪些层（以及它们对最终损失的贡献）对生成的可视化结果具有很大影响，
所以我们希望让这些参数变得易于配置。更靠近底部的层生成的是几何图案，而更靠近顶部的
层生成的则是从中能够看出某些ImageNet 类别（比如鸟或狗）的图案。我们将随意选择4 层的
配置，但你以后一定要探索多个不同的配置。

layer_contributions = {
'mixed2': 0.2,
'mixed3': 3.,
'mixed4': 2.,
'mixed5': 1.5,
}

创建一个字典，将层的名称
映射为层的实例

layer_dict = dict([(layer.name, layer) for layer in model.layers])
loss = K.variable(0.)
for layer_name in layer_contributions:
coeff = layer_contributions[layer_name]
activation = layer_dict[layer_name].output
scaling = K.prod(K.cast(K.shape(activation), 'float32'))
loss += coeff * K.sum(K.square(activation[:, 2: -2, 2: -2, :])) / scaling

下面来设置梯度上升过程。

dream = model.input
grads = K.gradients(loss, dream)[0]
grads /= K.maximum(K.mean(K.abs(grads)), 1e-7)
outputs = [loss, grads]
fetch_loss_and_grads = K.function([dream], outputs)
def eval_loss_and_grads(x):
outs = fetch_loss_and_grads([x])
loss_value = outs[0]
grad_values = outs[1]
return loss_value, grad_values
def gradient_ascent(x, iterations, step, max_loss=None):
for i in range(iterations):
loss_value, grad_values = eval_loss_and_grads(x)
if max_loss is not None and loss_value > max_loss:
break
print('...Loss value at', i, ':', loss_value)
x += step * grad_values
return x

最后就是实际的DeepDream 算法。首先，我们来定义一个列表，里面包含的是处理图像的
尺度（也叫八度）。每个连续的尺度都是前一个的1.4 倍（放大40%），即首先处理小图像，然
后逐渐增大图像尺寸（见图8-4）。

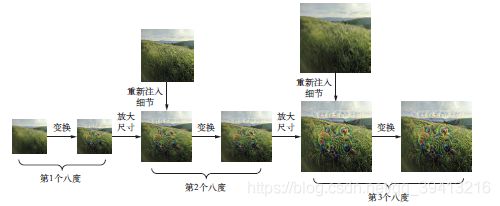
对于每个连续的尺度，从最小到最大，我们都需要在当前尺度运行梯度上升，以便将之前
定义的损失最大化。每次运行完梯度上升之后，将得到的图像放大40%。
在每次连续的放大之后（图像会变得模糊或像素化），为避免丢失大量图像细节，我们可
以使用一个简单的技巧：每次放大之后，将丢失的细节重新注入到图像中。这种方法是可行的，
因为我们知道原始图像放大到这个尺寸应该是什么样子。给定一个较小的图像尺寸S 和一个较
大的图像尺寸L，你可以计算将原始图像大小调整为L 与将原始图像大小调整为S 之间的区别，
这个区别可以定量描述从S 到L 的细节损失。

import numpy as np
step = 0.01
num_octave = 3
octave_scale = 1.4
iterations = 20
max_loss = 10.
base_image_path = '...'
img = preprocess_image(base_image_path)
original_shape = img.shape[1:3]
successive_shapes = [original_shape]
for i in range(1, num_octave):
shape = tuple([int(dim / (octave_scale ** i))
for dim in original_shape])
successive_shapes.append(shape)
successive_shapes = successive_shapes[::-1]
original_img = np.copy(img)
shrunk_original_img = resize_img(img, successive_shapes[0])
for shape in successive_shapes:
print('Processing image shape', shape)
img = resize_img(img, shape)
img = gradient_ascent(img,
iterations=iterations,
step=step,
max_loss=max_loss)
upscaled_shrunk_original_img = resize_img(shrunk_original_img, shape)
same_size_original = resize_img(original_img, shape)
lost_detail = same_size_original - upscaled_shrunk_original_img
img += lost_detail
shrunk_original_img = resize_img(original_img, shape)
save_img(img, fname='dream_at_scale_' + str(shape) + '.png')
save_img(img, fname='final_dream.png')

注意，上述代码使用了下面这些简单的Numpy 辅助函数，其功能从名称中就可以看出来。
它们都需要安装SciPy。

import scipy
from keras.preprocessing import image
def resize_img(img, size):
img = np.copy(img)
factors = (1,
float(size[0]) / img.shape[1],
float(size[1]) / img.shape[2],
1)
return scipy.ndimage.zoom(img, factors, order=1)
def save_img(img, fname):
pil_img = deprocess_image(np.copy(img))
scipy.misc.imsave(fname, pil_img)
def preprocess_image(image_path):
img = image.load_img(image_path)
img = image.img_to_array(img)
img = np.expand_dims(img, axis=0)
img = inception_v3.preprocess_input(img)
return img
def deprocess_image(x):
if K.image_data_format() == 'channels_first':
x = x.reshape((3, x.shape[2], x.shape[3]))
x = x.transpose((1, 2, 0))
else:
x = x.reshape((x.shape[1], x.shape[2], 3))
x /= 2.
x += 0.5
x *= 255.
x = np.clip(x, 0, 255).astype('uint8')
return x

最开始的照片是在旧金山湾和Google 校园之间的小山上拍摄的，我们从这张照片得到的
DeepDream 图像如下图。

我们强烈建议你调节在损失中使用的层，从而探索能够得到什么样的结果。网络中更靠近
底部的层包含更局部、不太抽象的表示，得到的梦境图案看起来更像是几何形状。更靠近顶部
的层能够得到更容易识别的视觉图案，这些图案都是基于ImageNet 中最常见的对象，比如狗
眼睛、鸟羽毛等。你可以随机生成layer_contributions 字典中的参数，从而快速探索多种不
同的层组合。对于一张自制美味糕点的图像，下面系列的图 给出了利用不同的层配置所得到的一系列结果。

三、神经风格迁移

除DeepDream 之外，深度学习驱动图像修改的另一项重大进展是神经风格迁移（neural
style transfer），它由Leon Gatys 等人于2015 年夏天提出。 自首次提出以来，神经风格迁移算
法已经做了许多改进，并衍生出许多变体，而且还成功转化成许多智能手机图片应用。为了简
单起见，本节将重点介绍原始论文中描述的方法。神经风格迁移是指将参考图像的风格应用于目标图像，同时保留目标图像的内容。下面是给出的一个示例。

风格是人类感知到的视觉感觉，包括不同的纹理颜色和视觉图案，内容是更高级的宏观结构。对于风格迁移来说，最大的难题是如何定义损失函数，这个损失函数不像分类预测那样简单，现在的损失函数如下：
loss = distance(style(reference_image) - style(generated_image)) +
distance(content(original_image) - content(generated_image))
这里的distance 是一个范数函数，比如L2 范数；content 是一个函数，输入一张图
像，并计算出其内容的表示；style 是一个函数，输入一张图像，并计算出其风格的表示。将
这个损失最小化，会使得style(generated_image) 接近于style(reference_image)、
content(generated_image) 接近于content(generated_image)，从而实现我们定义的
风格迁移。

1.内容损失

如你所知，网络更靠底部的层激活包含关于图像的局部信息，而更靠近顶部的层则包含更
加全局、更加抽象的信息。卷积神经网络不同层的激活用另一种方式提供了图像内容在不同空
间尺度上的分解。因此，图像的内容是更加全局和抽象的，我们认为它能够被卷积神经网络更
靠顶部的层的表示所捕捉到。
因此，内容损失的一个很好的候选者就是两个激活之间的L2 范数，一个激活是预训练的卷
积神经网络更靠顶部的某层在目标图像上计算得到的激活，另一个激活是同一层在生成图像上
计算得到的激活。这可以保证，在更靠顶部的层看来，生成图像与原始目标图像看起来很相似。
假设卷积神经网络更靠顶部的层看到的就是输入图像的内容，那么这种方法可以保存图像内容。

2.风格损失

内容损失只使用了一个更靠顶部的层，但Gatys 等人定义的风格损失则使用了卷积神经网
络的多个层。我们想要捉到卷积神经网络在风格参考图像的所有空间尺度上提取的外观，而不
仅仅是在单一尺度上。对于风格损失，Gatys 等人使用了层激活的格拉姆矩阵（Gram matrix），
即某一层特征图的内积。这个内积可以被理解成表示该层特征之间相互关系的映射。这些特征
相互关系抓住了在特定空间尺度下模式的统计规律，从经验上来看，它对应于这个尺度上找到
的纹理的外观。
因此，风格损失的目的是在风格参考图像与生成图像之间，在不同的层激活内保存相似的
内部相互关系。反过来，这保证了在风格参考图像与生成图像之间，不同空间尺度找到的纹理
看起来都很相似。
简而言之，你可以使用预训练的卷积神经网络来定义一个具有以下特点的损失。
‰ 在目标内容图像和生成图像之间保持相似的较高层激活，从而能够保留内容。卷积神经
网络应该能够“看到”目标图像和生成图像包含相同的内容。
‰ 在较低层和较高层的激活中保持类似的相互关系（correlation），从而能够保留风格。特
征相互关系捕捉到的是纹理（texture），生成图像和风格参考图像在不同的空间尺度上应
该具有相同的纹理。
接下来，我们来用Keras 实现2015 年的原始神经风格迁移算法。你将会看到，它与上一节
介绍的DeepDream 算法实现有许多相似之处。

3.用Keras 实现神经风格迁移

神经风格迁移可以用任何预训练卷积神经网络来实现。我们这里将使用Gatys 等人所使用
的VGG19 网络。VGG19 是第5 章介绍的VGG16 网络的简单变体，增加了三个卷积层。
神经风格迁移的一般过程如下。
(1) 创建一个网络，它能够同时计算风格参考图像、目标图像和生成图像的VGG19 层激活。
(2) 使用这三张图像上计算的层激活来定义之前所述的损失函数，为了实现风格迁移，需要
将这个损失函数最小化。
(3) 设置梯度下降过程来将这个损失函数最小化。
我们首先来定义风格参考图像和目标图像的路径。为了确保处理后的图像具有相似的尺寸
（如果图像尺寸差异很大，会使得风格迁移变得更加困难），稍后需要将所有图像的高度调整为
400 像素。

from keras.preprocessing.image import load_img, img_to_array
target_image_path = 'img/portrait.jpg'
style_reference_image_path = 'img/transfer_style_reference.jpg'
width, height = load_img(target_image_path).size
img_height = 400
img_width = int(width * img_height / height)
import numpy as np
from keras.applications import vgg19
def preprocess_image(image_path):
img = load_img(image_path, target_size=(img_height, img_width))
img = img_to_array(img)
img = np.expand_dims(img, axis=0)
img = vgg19.preprocess_input(img)
return img
def deprocess_image(x):
x[:, :, 0] += 103.939
x[:, :, 1] += 116.779
x[:, :, 2] += 123.68
x = x[:, :, ::-1]
x = np.clip(x, 0, 255).astype('uint8')
return x

下面构建VGG19 网络。它接收三张图像的批量作为输入，三张图像分别是风格参考图像、
目标图像和一个用于保存生成图像的占位符。占位符是一个符号张量，它的值由外部Numpy 张
量提供。风格参考图像和目标图像都是不变的，因此使用K.constant 来定义，但生成图像的
占位符所包含的值会随着时间而改变。

from keras import backend as K
target_image = K.constant(preprocess_image(target_image_path))
style_reference_image = K.constant(preprocess_image(style_reference_image_path))
combination_image = K.placeholder((1, img_height, img_width, 3))
input_tensor = K.concatenate([target_image,
style_reference_image,
combination_image], axis=0)
model = vgg19.VGG19(input_tensor=input_tensor,
weights='imagenet',
include_top=False)
print('Model loaded.')

我们来定义内容损失，它要保证目标图像和生成图像在VGG19 卷积神经网络的顶层具有相
似的结果。

def content_loss(base, combination):
    return K.sum(K.square(combination - base))

接下来是风格损失。它使用一个辅助函数来计算输入矩阵的格拉姆矩阵，即原始特征矩阵
中相互关系的映射。

def gram_matrix(x):
features = K.batch_flatten(K.permute_dimensions(x, (2, 0, 1)))
gram = K.dot(features, K.transpose(features))
return gram
def style_loss(style, combination):
S = gram_matrix(style)
C = gram_matrix(combination)
channels = 3
size = img_height * img_width
return K.sum(K.square(S - C)) / (4. * (channels ** 2) * (size ** 2))

除了这两个损失分量，我们还要添加第三个——总变差损失（total variation loss），它对生成
的组合图像的像素进行操作。它促使生成图像具有空间连续性，从而避免结果过度像素化。你
可以将其理解为正则化损失。

def total_variation_loss(x):
a = K.square(
x[:, :img_height - 1, :img_width - 1, :] -
x[:, 1:, :img_width - 1, :])
b = K.square(
x[:, :img_height - 1, :img_width - 1, :] -
x[:, :img_height - 1, 1:, :])
return K.sum(K.pow(a + b, 1.25))

我们需要最小化的损失是这三项损失的加权平均。为了计算内容损失，我们只使用一个靠
顶部的层，即block5_conv2 层；而对于风格损失，我们需要使用一系列层，既包括顶层也包
括底层。最后还需要添加总变差损失。
根据所使用的风格参考图像和内容图像，很可能还需要调节content_weight 系数（内容
损失对总损失的贡献比例）。更大的content_weight 表示目标内容更容易在生成图像中被识
别出来。

outputs_dict = dict([(layer.name, layer.output) for layer in model.layers])
content_layer = 'block5_conv2'
style_layers = ['block1_conv1',
'block2_conv1',
'block3_conv1',
'block4_conv1',
'block5_conv1']
total_variation_weight = 1e-4
style_weight = 1.
content_weight = 0.025
loss = K.variable(0.)
layer_features = outputs_dict[content_layer]
target_image_features = layer_features[0, :, :, :]
combination_features = layer_features[2, :, :, :]
loss += content_weight * content_loss(target_image_features,
combination_features)
for layer_name in style_layers:
layer_features = outputs_dict[layer_name]
style_reference_features = layer_features[1, :, :, :]
combination_features = layer_features[2, :, :, :]
sl = style_loss(style_reference_features, combination_features)
loss += (style_weight / len(style_layers)) * sl
loss += total_variation_weight * total_variation_loss(combination_image)

最后需要设置梯度下降过程。在Gatys 等人最初的论文中，使用L-BFGS 算法进行最优化，
所以我们这里也将使用这种方法。这是本例与8.2 节DeepDream 例子的主要区别。L-BFGS 算
法内置于SciPy 中，但SciPy 实现有两个小小的限制。
‰ 它需要将损失函数值和梯度值作为两个单独的函数传入。
‰ 它只能应用于展平的向量，而我们的数据是三维图像数组。
分别计算损失函数值和梯度值是很低效的，因为这么做会导致二者之间大量的冗余计算。
这一过程需要的时间几乎是联合计算二者所需时间的2 倍。为了避免这种情况，我们将创建一
个名为Evaluator 的Python 类，它可以同时计算损失值和梯度值，在第一次调用时会返回损
失值，同时缓存梯度值用于下一次调用。

grads = K.gradients(loss, combination_image)[0]
fetch_loss_and_grads = K.function([combination_image], [loss, grads])
class Evaluator(object):
def __init__(self):
self.loss_value = None
self.grads_values = None
def loss(self, x):
assert self.loss_value is None
x = x.reshape((1, img_height, img_width, 3))
outs = fetch_loss_and_grads([x])
loss_value = outs[0]
grad_values = outs[1].flatten().astype('float64')
self.loss_value = loss_value
self.grad_values = grad_values
return self.loss_value
def grads(self, x):
assert self.loss_value is not None
grad_values = np.copy(self.grad_values)
self.loss_value = None
self.grad_values = None
return grad_values
evaluator = Evaluator()

from scipy.optimize import fmin_l_bfgs_b
from scipy.misc import imsave
import time
result_prefix = 'my_result'
iterations = 20
x = preprocess_image(target_image_path)
x = x.flatten()
for i in range(iterations):
print('Start of iteration', i)
start_time = time.time()
x, min_val, info = fmin_l_bfgs_b(evaluator.loss,
x,
fprime=evaluator.grads,
maxfun=20)
print('Current loss value:', min_val)
img = x.copy().reshape((img_height, img_width, 3))
img = deprocess_image(img)
fname = result_prefix + '_at_iteration_%d.png' % i
imsave(fname, img)
print('Image saved as', fname)
end_time = time.time()
print('Iteration %d completed in %ds' % (i, end_time - start_time))

最后，可以使用SciPy 的L-BFGS 算法来运行梯度上升过程，在算法每一次迭代时都保存
当前的生成图像（这里一次迭代表示20 个梯度上升步骤）。

得到的结果如图8-8 所示。请记住，这种技术所实现的仅仅是一种形式的改变图像纹理，
或者叫纹理迁移。如果风格参考图像具有明显的纹理结构且高度自相似，并且内容目标不需要
高层次细节就能够被识别，那么这种方法的效果最好。它通常无法实现比较抽象的迁移，比如
将一幅肖像的风格迁移到另一幅中。这种算法更接近于经典的信号处理，而不是更接近于人工
智能，因此不要指望它能实现魔法般的效果。

此外还请注意，这个风格迁移算法的运行速度很慢。但这种方法实现的变换足够简单，只
要有适量的训练数据，一个小型的快速前馈卷积神经网络就可以学会这种变换。因此，实现快
速风格迁移的方法是，首先利用这里介绍的方法，花费大量的计算时间对一张固定的风格参考
图像生成许多输入- 输出训练样例，然后训练一个简单的卷积神经网络来学习这个特定风格的
变换。一旦完成之后，对一张图像进行风格迁移是非常快的，只是这个小型卷积神经网络的一
次前向传递而已。

四、用变分自编码器生成图像

从图像的潜在空间中采样，并创建全新图像或编辑现有图像，这是目前最流行也是最成
功的创造性人工智能应用。在本节和下一节中，我们将会介绍一些与图像生成有关的高级概
念，还会介绍该领域中两种主要技术的实现细节，这两种技术分别是变分自编码器（VAE，
variational autoencoder）和生成式对抗网络（GAN，generative adversarial network）。我们这里介
绍的技术不仅适用于图像，使用GAN 和VAE 还可以探索声音、音乐甚至文本的潜在空间，但
在实践中，最有趣的结果都是利用图像获得的，这也是我们这里介绍的重点。

1.从图像的潜在空间中采样

图像生成的关键思想就是找到一个低维的表示潜在空间（latent space，也是一个向量空间），
其中任意点都可以被映射为一张逼真的图像。能够实现这种映射的模块，即以潜在点作为输入
并输出一张图像（像素网格），叫作生成器（generator，对于GAN 而言）或解码器（decoder，
对于VAE 而言）。一旦找到了这样的潜在空间，就可以从中有意地或随机地对点进行采样，并
将其映射到图像空间，从而生成前所未见的图像。

想要学习图像表示的这种潜在空间，GAN 和VAE 是两种不同的策略，每种策略都有各自
的特点。VAE 非常适合用于学习具有良好结构的潜在空间，其中特定方向表示数据中有意义的
变化轴。GAN 生成的图像可能非常逼真，但它的潜在空间可能没有良好结构，也没有足够的连续性。

2.图像编辑的概念向量

第6 章介绍词嵌入时，我们已经暗示了概念向量（concept vector）的想法：给定一个表示
的潜在空间或一个嵌入空间，空间中的特定方向可能表示原始数据中有趣的变化轴。比如在人
脸图像的潜在空间中，可能存在一个微笑向量（smile vector）s，它满足：如果潜在点z 是某张
人脸的嵌入表示，那么潜在点z+s 就是同一张人脸面带微笑的嵌入表示。一旦找到了这样的向量，
就可以用这种方法来编辑图像：将图像投射到潜在空间中，用一种有意义的方式来移动其表示，
然后再将其解码到图像空间。在图像空间中任意独立的变化维度都有概念向量，对于人脸而言，
你可能会发现向人脸添加墨镜的向量、去掉墨镜的向量。将男性面孔变成女性面孔的向量等。
图8-11 是一个微笑向量的例子，它是由新西兰维多利亚大学设计学院的Tom White 发现的概念
向量，使用的是在名人人脸数据集（CelebA 数据集）上训练的VAE。

3.变分自编码器

自编码器由Kingma 和Welling 于2013 年12 月a 与Rezende、Mohamed 和Wierstra 于2014
年1 月b 同时发现，它是一种生成式模型，特别适用于利用概念向量进行图像编辑的任务。它是
一种现代化的自编码器，将深度学习的想法与贝叶斯推断结合在一起。自编码器是一种网络类型，
其目的是将输入编码到低维潜在空间，然后再解码回来。
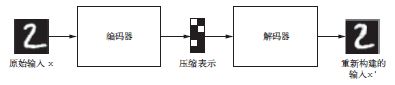
经典的图像自编码器接收一张图像，通过一个编码器模块将其映射到潜在向量空间，然后
再通过一个解码器模块将其解码为与原始图像具有相同尺寸的输出（见图8-12）。然后，使用与
输入图像相同的图像作为目标数据来训练这个自编码器，也就是说，自编码器学习对原始输入
进行重新构建。通过对代码（编码器的输出）施加各种限制，我们可以让自编码器学到比较有
趣的数据潜在表示。最常见的情况是将代码限制为低维的并且是稀疏的（即大部分元素为0），
在这种情况下，编码器的作用是将输入数据压缩为更少二进制位的信息。

在实践中，这种经典的自编码器不会得到特别有用或具有良好结构的潜在空间。它们也没
有对数据做多少压缩。因此，它们已经基本上过时了。但是，VAE 向自编码器添加了一点统计
魔法，迫使其学习连续的、高度结构化的潜在空间。这使得VAE 已成为图像生成的强大工具。
VAE 不是将输入图像压缩成潜在空间中的固定编码，而是将图像转换为统计分布的参数，
即平均值和方差。本质上来说，这意味着我们假设输入图像是由统计过程生成的，在编码和解
码过程中应该考虑这一过程的随机性。然后，VAE 使用平均值和方差这两个参数来从分布中随
机采样一个元素，并将这个元素解码到原始输入（见图8-13）。这个过程的随机性提高了其稳健
性，并迫使潜在空间的任何位置都对应有意义的表示，即潜在空间采样的每个点都能解码为有
效的输出。

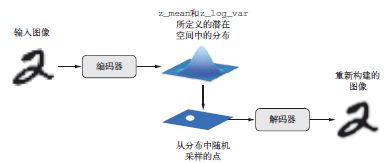
从技术角度来说，VAE 的工作原理如下。
(1) 一个编码器模块将输入样本input_img 转换为表示潜在空间中的两个参数z_mean 和
z_log_variance。
(2) 我们假定潜在正态分布能够生成输入图像，并从这个分布中随机采样一个点z：z =
z_mean + exp(z_log_variance) * epsilon，其中epsilon 是取值很小的随机
张量。
(3) 一个解码器模块将潜在空间的这个点映射回原始输入图像。
因为epsilon 是随机的，所以这个过程可以确保，与input_img 编码的潜在位置（即
z-mean）靠近的每个点都能被解码为与input_img 类似的图像，从而迫使潜在空间能够连续
地有意义。潜在空间中任意两个相邻的点都会被解码为高度相似的图像。连续性以及潜在空间
的低维度，将迫使潜在空间中的每个方向都表示数据中一个有意义的变化轴，这使得潜在空间
具有非常良好的结构，因此非常适合通过概念向量来进行操作。
VAE 的参数通过两个损失函数来进行训练：一个是重构损失（reconstruction loss），它迫
使解码后的样本匹配初始输入；另一个是正则化损失（regularization loss），它有助于学习具有
良好结构的潜在空间，并可以降低在训练数据上的过拟合。我们来快速浏览一下Keras 实现的
VAE。其大致代码如下所示。

z_mean, z_log_variance = encoder(input_img)
z = z_mean + exp(z_log_variance) * epsilon
reconstructed_img = decoder(z)
model = Model(input_img, reconstructed_img)

然后，你可以使用重构损失和正则化损失来训练模型。
下列代码给出了我们将使用的编码器网络，它将图像映射为潜在空间中概率分布的参数。
它是一个简单的卷积神经网络，将输入图像x 映射为两个向量z_mean 和z_log_var。

import keras
from keras import layers
from keras import backend as K
from keras.models import Model
import numpy as np
img_shape = (28, 28, 1)
batch_size = 16
latent_dim = 2
input_img = keras.Input(shape=img_shape)
x = layers.Conv2D(32, 3,
padding='same', activation='relu')(input_img)
x = layers.Conv2D(64, 3,
padding='same', activation='relu',
strides=(2, 2))(x)
x = layers.Conv2D(64, 3,
padding='same', activation='relu')(x)
x = layers.Conv2D(64, 3,
padding='same', activation='relu')(x)
shape_before_flattening = K.int_shape(x)
x = layers.Flatten()(x)
x = layers.Dense(32, activation='relu')(x)
z_mean = layers.Dense(latent_dim)(x)
z_log_var = layers.Dense(latent_dim)(x)

接下来的代码将使用z_mean 和z_log_var 来生成一个潜在空间点z，z_mean 和z_log_
var 是统计分布的参数，我们假设这个分布能够生成input_img。这里，我们将一些随意的代
码（这些代码构建于Keras 后端之上）包装到Lambda 层中。在Keras 中，任何对象都应该是一
个层，所以如果代码不是内置层的一部分，我们应该将其包装到一个Lambda 层（或自定义层）中。

def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim),
mean=0., stddev=1.)
return z_mean + K.exp(z_log_var) * epsilon
z = layers.Lambda(sampling)([z_mean, z_log_var])

下列代码给出了解码器的实现。我们将向量z 的尺寸调整为图像大小，然后使用几个卷积
层来得到最终的图像输出，它和原始图像input_img 具有相同的大小。

decoder_input = layers.Input(K.int_shape(z)[1:])
x = layers.Dense(np.prod(shape_before_flattening[1:]),
activation='relu')(decoder_input)
x = layers.Reshape(shape_before_flattening[1:])(x)
x = layers.Conv2DTranspose(32, 3,
padding='same',
activation='relu',
strides=(2, 2))(x)
x = layers.Conv2D(1, 3,
padding='same',
activation='sigmoid')(x)
decoder = Model(decoder_input, x)
z_decoded = decoder(z)

我们一般认为采样函数的形式为loss(input, target)，VAE 的双重损失不符合这种形
式。因此，损失的设置方法为：编写一个自定义层，并在其内部使用内置的add_loss 层方法
来创建一个你想要的损失。

class CustomVariationalLayer(keras.layers.Layer):
def vae_loss(self, x, z_decoded):
x = K.flatten(x)
z_decoded = K.flatten(z_decoded)
xent_loss = keras.metrics.binary_crossentropy(x, z_decoded)
kl_loss = -5e-4 * K.mean(
1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
return K.mean(xent_loss + kl_loss)
def call(self, inputs):
x = inputs[0]
z_decoded = inputs[1]
loss = self.vae_loss(x, z_decoded)
self.add_loss(loss, inputs=inputs)
return x
y = CustomVariationalLayer()([input_img, z_decoded])

最后，将模型实例化并开始训练。因为损失包含在自定义层中，所以在编译时无须指定外
部损失（即loss=None），这意味着在训练过程中不需要传入目标数据。（如你所见，我们在调
用fit 时只向模型传入了x_train。）

from keras.datasets import mnist
vae = Model(input_img, y)
vae.compile(optimizer='rmsprop', loss=None)
vae.summary()
(x_train, _), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_train = x_train.reshape(x_train.shape + (1,))
x_test = x_test.astype('float32') / 255.
x_test = x_test.reshape(x_test.shape + (1,))
vae.fit(x=x_train, y=None,
shuffle=True,
epochs=10,
batch_size=batch_size,
validation_data=(x_test, None))

一旦训练好了这样的模型（本例中是在MNIST 上训练），我们就可以使用decoder 网络将
任意潜在空间向量转换为图像。

import matplotlib.pyplot as plt
from scipy.stats import norm
n = 15
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z_sample = np.array([[xi, yi]])
z_sample = np.tile(z_sample, batch_size).reshape(batch_size, 2)
x_decoded = decoder.predict(z_sample, batch_size=batch_size)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap='Greys_r')
plt.show()

采样数字的网格（见图8-14）展示了不同数字类别的完全连续分布：当你沿着潜在空间的
一条路径观察时，你会观察到一个数字逐渐变形为另一个数字。这个空间的特定方向具有一定
的意义，比如，有一个方向表示“逐渐变为4”、有一个方向表示“逐渐变为1”等。
下一节我们将会详细介绍生成人造图像的另一个重要工具，即生成式对抗网络（GAN）。

五、生成式对抗网络简介

生成式对抗网络（GAN，generative adversarial network）由Goodfellow 等人于2014 年提
出a，它可以替代VAE 来学习图像的潜在空间。它能够迫使生成图像与真实图像在统计上几乎无
法区分，从而生成相当逼真的合成图像。
对GAN 的一种直观理解是，想象一名伪造者试图伪造一副毕加索的画作。一开始，伪造者
非常不擅长这项任务。他将自己的一些赝品与毕加索真迹混在一起，并将其展示给一位艺术商人。
艺术商人对每幅画进行真实性评估，并向伪造者给出反馈，告诉他是什么让毕加索作品看起来
像一幅毕加索作品。伪造者回到自己的工作室，并准备一些新的赝品。随着时间的推移，伪造
者变得越来越擅长模仿毕加索的风格，艺术商人也变得越来越擅长找出赝品。最后，他们手上
拥有了一些优秀的毕加索赝品。
这就是GAN 的工作原理：一个伪造者网络和一个专家网络，二者训练的目的都是为了打败
彼此。因此，GAN 由以下两部分组成。
‰ 生成器网络（generator network）：它以一个随机向量（潜在空间中的一个随机点）作
为输入，并将其解码为一张合成图像。
‰ 判别器网络（discriminator network）或对手（adversary）：以一张图像（真实的或合成的
均可）作为输入，并预测该图像是来自训练集还是由生成器网络创建。
训练生成器网络的目的是使其能够欺骗判别器网络，因此随着训练的进行，它能够逐渐生
成越来越逼真的图像，即看起来与真实图像无法区分的人造图像，以至于判别器网络无法区分二
者。与此同时，判别器也在不断适应生成器逐渐提高的能力，为生成图像的真实性
设置了很高的标准。一旦训练结束，生成器就能够将其输入空间中的任何点转换为一张可信图像
。与VAE 不同，这个潜在空间无法保证具有有意义的结构，而且它还是不连续的。

值得注意的是，GAN 这个系统与本书中其他任何训练方法都不同，它的优化最小值是不固
定的。通常来说，梯度下降是沿着静态的损失地形滚下山坡。但对于GAN 而言，每下山一步，
都会对整个地形造成一点改变。它是一个动态的系统，其最优化过程寻找的不是一个最小值，
而是两股力量之间的平衡。因此，GAN 的训练极其困难，想要让GAN 正常运行，需要对模型
架构和训练参数进行大量的仔细调整

1.GAN 的简要实现流程

本节将会介绍如何用Keras 来实现形式最简单的GAN。GAN 属于高级应用，所以本书
不会深入介绍其技术细节。我们具体实现的是一个深度卷积生成式对抗网络（DCGAN，deep
convolutional GAN），即生成器和判别器都是深度卷积神经网络的GAN。特别地，它在生成器中
使用Conv2DTranspose 层进行图像上采样。
我们将在CIFAR10 数据集的图像上训练GAN，这个数据集包含50 000 张32×32 的RGB
图像，这些图像属于10 个类别（每个类别5000 张图像）。为了简化，我们只使用属于“frog”（青
蛙）类别的图像。
GAN 的简要实现流程如下所示。
(1) generator 网络将形状为(latent_dim,) 的向量映射到形状为(32, 32, 3) 的图像。
(2) discriminator 网络将形状为(32, 32, 3) 的图像映射到一个二进制分数，用于评
估图像为真的概率。
(3) gan 网络将generator 网络和discriminator 网络连接在一起：gan(x) = discriminator
(generator(x))。生成器将潜在空间向量解码为图像，判别器对这些图像的真实性进
行评估，因此这个gan 网络是将这些潜在向量映射到判别器的评估结果。
(4) 我们使用带有“真”/“假”标签的真假图像样本来训练判别器，就和训练普通的图像
分类模型一样。
(5) 为了训练生成器，我们要使用gan 模型的损失相对于生成器权重的梯度。这意味着，
在每一步都要移动生成器的权重，其移动方向是让判别器更有可能将生成器解码的图像
划分为“真”。换句话说，我们训练生成器来欺骗判别器。

2.大量技巧

训练GAN 和调节GAN 实现的过程非常困难。你应该记住一些公认的技巧。与深度学习中
的大部分内容一样，这些技巧更像是炼金术而不是科学，它们是启发式的指南，并没有理论上
的支持。这些技巧得到了一定程度的来自对现象的直观理解的支持，经验告诉我们，它们的效
果都很好，但不一定适用于所有情况。
下面是本节实现GAN 生成器和判别器时用到的一些技巧。这里并没有列出与GAN 相关的
全部技巧，更多技巧可查阅关于GAN 的文献。
‰ 我们使用 tanh作为生成器最后一层的激活，而不用 sigmoid，后者在其他类型的模型中
更加常见。
‰ 我们使用正态分布（高斯分布）对潜在空间中的点进行采样，而不用均匀分布。
‰ 随机性能够提高稳健性。训练GAN得到的是一个动态平衡，所以GAN可能以各种方式“卡
住”。在训练过程中引入随机性有助于防止出现这种情况。我们通过两种方式引入随机性：
一种是在判别器中使用dropout，另一种是向判别器的标签添加随机噪声。
‰ 稀疏的梯度会妨碍 GAN 的训练。在深度学习中，稀疏性通常是我们需要的属性，但在
GAN 中并非如此。有两件事情可能导致梯度稀疏：最大池化运算和ReLU 激活。我们推
荐使用步进卷积代替最大池化来进行下采样，还推荐使用LeakyReLU 层来代替ReLU 激
活。LeakyReLU 和ReLU 类似，但它允许较小的负数激活值，从而放宽了稀疏性限制。
‰ 在生成的图像中，经常会见到棋盘状伪影，这是由生成器中像素空间的不均匀覆盖导致的
（见图8-17）。为了解决这个问题，每当在生成器和判别器中都使用步进的Conv2DTranpose
或Conv2D 时，使用的内核大小要能够被步幅大小整除。

3.生成器

首先，我们来开发generator 模型，它将一个向量（来自潜在空间，训练过程中对其随机
采样）转换为一张候选图像。GAN 常见的诸多问题之一，就是生成器“卡在”看似噪声的生成
图像上。一种可行的解决方案是在判别器和生成器中都使用dropout。

import keras
from keras import layers
import numpy as np
latent_dim = 32
height = 32
width = 32
channels = 3
generator_input = keras.Input(shape=(latent_dim,))
x = layers.Dense(128 * 16 * 16)(generator_input)
x = layers.LeakyReLU()(x)
x = layers.Reshape((16, 16, 128))(x)
x = layers.Conv2D(256, 5, padding='same')(x)
x = layers.LeakyReLU()(x)
x = layers.Conv2DTranspose(256, 4, strides=2, padding='same')(x)
x = layers.LeakyReLU()(x)
x = layers.Conv2D(256, 5, padding='same')(x)
x = layers.LeakyReLU()(x)
x = layers.Conv2D(256, 5, padding='same')(x)
x = layers.LeakyReLU()(x)
x = layers.Conv2D(channels, 7, activation='tanh', padding='same')(x)
generator = keras.models.Model(generator_input, x)
generator.summary()

4.判别器

接下来，我们来开发discriminator 模型，它接收一张候选图像（真实的或合成的）作
为输入，并将其划分到这两个类别之一：“生成图像”或“来自训练集的真实图像”。

discriminator_input = layers.Input(shape=(height, width, channels))
x = layers.Conv2D(128, 3)(discriminator_input)
x = layers.LeakyReLU()(x)
x = layers.Conv2D(128, 4, strides=2)(x)
x = layers.LeakyReLU()(x)
x = layers.Conv2D(128, 4, strides=2)(x)
x = layers.LeakyReLU()(x)
x = layers.Conv2D(128, 4, strides=2)(x)
x = layers.LeakyReLU()(x)
x = layers.Flatten()(x)
x = layers.Dropout(0.4)(x)
x = layers.Dense(1, activation='sigmoid')(x)
discriminator = keras.models.Model(discriminator_input, x)
discriminator.summary()
discriminator_optimizer = keras.optimizers.RMSprop(
lr=0.0008,
clipvalue=1.0,
decay=1e-8)
discriminator.compile(optimizer=discriminator_optimizer,
loss='binary_crossentropy')

5.对抗网络

最后，我们要设置GAN，将生成器和判别器连接在一起。训练时，这个模型将让生成器向
某个方向移动，从而提高它欺骗判别器的能力。这个模型将潜在空间的点转换为一个分类决策（即
“真”或“假”），它训练的标签都是“真实图像”。因此，训练gan 将会更新generator 的权重，
使得discriminator 在观察假图像时更有可能预测为“真”。请注意，有一点很重要，就是在
训练过程中需要将判别器设置为冻结（即不可训练），这样在训练gan 时它的权重才不会更新。
如果在此过程中可以对判别器的权重进行更新，那么我们就是在训练判别器始终预测“真”，但
这并不是我们想要的！

discriminator.trainable = False
gan_input = keras.Input(shape=(latent_dim,))
gan_output = discriminator(generator(gan_input))
gan = keras.models.Model(gan_input, gan_output)
gan_optimizer = keras.optimizers.RMSprop(lr=0.0004, clipvalue=1.0, decay=1e-8)
gan.compile(optimizer=gan_optimizer, loss='binary_crossentropy')

6.训练网络

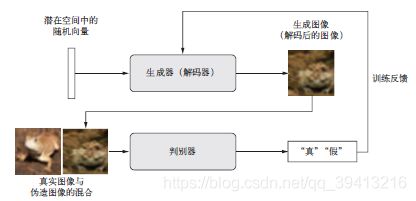
现在开始训练。再次强调一下，训练循环的大致流程如下所示。每轮都进行以下操作。
(1) 从潜在空间中抽取随机的点（随机噪声）。
(2) 利用这个随机噪声用generator 生成图像。
(3) 将生成图像与真实图像混合。
(4) 使用这些混合后的图像以及相应的标签（真实图像为“真”，生成图像为“假”）来训练
discriminator，如图8-18 所示。
(5) 在潜在空间中随机抽取新的点。
(6) 使用这些随机向量以及全部是“真实图像”的标签来训练gan。这会更新生成器的权重
（只更新生成器的权重，因为判别器在gan 中被冻结），其更新方向是使得判别器能够
将生成图像预测为“真实图像”。这个过程是训练生成器去欺骗判别器。
我们来实现这一流程。

import os
from keras.preprocessing import image
(x_train, y_train), (_, _) = keras.datasets.cifar10.load_data()
x_train = x_train[y_train.flatten() == 6]
x_train = x_train.reshape(
(x_train.shape[0],) +
(height, width, channels)).astype('float32') / 255.
iterations = 10000
batch_size = 20
save_dir = 'your_dir'
start = 0
for step in range(iterations):
random_latent_vectors = np.random.normal(size=(batch_size,
latent_dim))
generated_images = generator.predict(random_latent_vectors)
stop = start + batch_size
real_images = x_train[start: stop]
combined_images = np.concatenate([generated_images, real_images])
labels = np.concatenate([np.ones((batch_size, 1)),
np.zeros((batch_size, 1))])
labels += 0.05 * np.random.random(labels.shape)
d_loss = discriminator.train_on_batch(combined_images, labels)
random_latent_vectors = np.random.normal(size=(batch_size,
latent_dim))
misleading_targets = np.zeros((batch_size, 1))
a_loss = gan.train_on_batch(random_latent_vectors,
misleading_targets)
start += batch_size
if start > len(x_train) - batch_size:
start = 0
if step % 100 == 0:
gan.save_weights('gan.h5')
print('discriminator loss:', d_loss)
print('adversarial loss:', a_loss)
img = image.array_to_img(generated_images[0] * 255., scale=False)
img.save(os.path.join(save_dir,
'generated_frog' + str(step) + '.png'))
img = image.array_to_img(real_images[0] * 255., scale=False)
img.save(os.path.join(save_dir,
'real_frog' + str(step) + '.png'))

训练时你可能会看到，对抗损失开始大幅增加，而判别损失则趋向于零，即判别器最终支配
了生成器。如果出现了这种情况，你可以尝试减小判别器的学习率，并增大判别器的dropout 比率。

data = pd.read_csv(
    'https://labfile.oss.aliyuncs.com/courses/1283/adult.data.csv')
print(data.head())

总结

借助深度学习的创造性应用，深度网络不仅能够对现有内容进行标注，还能够自己生成
新内容。本章我们学到的内容如下。
ƒ 如何生成序列数据，每次生成一个时间步。这可以应用于文本生成，也可应用于逐个
音符的音乐生成或其他任何类型的时间序列数据。
ƒ DeepDream 的工作原理：通过输入空间中的梯度上升将卷积神经网络的层激活最大化。
ƒ 如何实现风格迁移，即将内容图像和风格图像组合在一起，并产生有趣的效果。
ƒ 什么是对抗式生成网络（GAN），什么是变分自编码器（VAE），它们如何用于创造新
图像，以及如何使用潜在空间概念向量进行图像编辑。
‰ 这几项技术仅涉及了这一快速发展领域的基础知识，还有许多内容等待你去探索。仅生
成式深度学习这一领域的内容就可以写一整本书。