K-means聚类 实验报告

1. 任务定义

• 使用K-means模型对cluster.dat进行聚类。尝试使用不同的类别个数K，并分析聚类结果。
• 按照 8:2 的比例，随机将数据划分为训练集和测试集。至少尝试 3 个不同的 K 值，并画出不同 K 下的聚类结果，及不同模型在训练集和测试集上的损失。对结果进行讨论，发现能解释数据的最好的 K 值。

2. 实验环境

• Windows 10
• VS Code
• python 3.7.8

3. 方法描述

3.1 数据切分

• 输入：data：原数据列表，shuffle：是否随机切分 ，ratio：测试集比例
• 输出：train_data：训练集，test_data：测试集
• 方法：使用random.shuffle()对数据进行洗牌，再按比例取出

# data:原数据列表  shuffle:是否随机切分 ratio:测试集比例
def split(data, shuffle=False, ratio=0.2):
    n = len(data)
    offset = int(n * ratio)

    if n == 0 or offset < 1:
        return data, []
    if shuffle:
    	# 对数据进行洗牌
        random.shuffle(data)
	
	# 按比例取出训练集和测试集
    train_data = data[offset:]
    test_data  = data[:offset]

    return train_data, test_data

3.2 模型训练

3.2.1 读取数据

def loadData(filename):
    data = np.loadtxt(filename)
    
    return data

3.2.2 初始化K个中心点

• 输入：data：数据列表，k：中心点个数
• 输出：Cpoints：中心点坐标列表
• 方法：在数据中随机选取k个点作为初始中心点

def randomCent(data, k):
    m, n = data.shape
    Cpoints = np.zeros((k, n))
    indexs  = np.random.uniform(0, m, k)

    for i in range(len(indexs)):
        Cpoints[i,:] = data[int(indexs[i]),:]

    return Cpoints

3.2.3 计算点到聚类中心点的距离

• 输入：x：点1，y：点2，method：计算距离方法（E:欧式距离, M:曼哈顿距离, C:余弦距离 默认为欧式距离）
• 输出：两点之间的距离
• 方法：根据选取的计算距离方法调用对应的函数进行计算

# E:欧式距离, M:曼哈顿距离, C:余弦距离 默认为欧式距离
def distance(x, y, method='E'):
    if method == 'E':
        dist = distE(x, y)
    elif method == 'M':
        dist = distM(x, y)
    elif method == 'C':
        dist = distC(x, y)
        
    return dist

• 欧式距离：$dist(x,y)=\sqrt{{\sum }_{i=1}^n(x_i-y_i{)}^2}$，即求L2范数

# 计算欧式距离
def distE(x, y):
    return np.linalg.norm(x - y, ord=2)

• 曼哈顿距离：$dist(x,y)={\sum }_{i=1}^n|x_i-y_i|$，即求L1范数

# 计算曼哈顿距离
def distM(x, y):
    return np.linalg.norm(x - y, ord=1)

• 余弦距离：$dist(x,y)=\frac{{\sum }_{i=1}^n{x}_i{y}_i}{\sqrt{{\sum }_{i=1}^n{x}_i^2}\sqrt{{\sum }_{i=1}^n{y}_i^2}}$

# 计算余弦距离
def distC(x, y):
    Matrix_Mul = np.dot(x, y)
    x_l2 = np.linalg.norm(x, ord=2)
    y_l2 = np.linalg.norm(y, ord=2)
    dist = 1 - Matrix_Mul / (x_l2 * y_l2)

    return dist

3.2.4 模型训练

• 输入：data：数据列表，k：类的个数，method：距离计算方法（默认为欧式距离）
• 输出：clusters：聚类结果，Cpoints：中心点坐标

def KMeans(data, k, method='E'):

• 获取数据维度，初始化聚类结果、中心点、聚类标志Flag

    m, n = data.shape
    clusters = np.zeros(m)
    Cpoints  = randomCent(data, k)
    Flag = True

• 当聚类标志为True时进行聚类
• 遍历每一个待聚类点

    while Flag:
        Flag = False
        
        # 遍历每一个点
        for i in range(m):
            minDist  = float("inf")
            minIndex = -1

• 寻找每个点距离最近的中心点

            # 寻找最近的中心点
            for j in range(k):
                # 计算该点到中心点的距离，默认为欧式距离
                dist = distance(Cpoints[j,:], data[i,:], method)
                if dist < minDist:
                    minDist  = dist
                    minIndex = j

• 根据最近的中心点更新每个点所属的簇

            # 更新每个点所属的簇
            if clusters[i] != minIndex:
                Flag = True
                clusters[i] = minIndex

• 计算簇中所有点的均值，获取新的中心点

        # 更新中心点
        for i in range(k):
            # 获取簇中所有的点
            ClusterPoints = data[clusters == i]   
            # 根据均值获取中心点的位置
            Cpoints[i,:]  = np.mean(ClusterPoints, axis=0)

• 返回结果

    return clusters, Cpoints

3.2.5 绘制聚类图

def showClusters(data, k, Cpoints, clusters):
    m, n = data.shape
    
    # mark为颜色代号
    mark = ['or', 'ob', 'og', 'ok', 'vr', 'vb', 'vg', 'vk'] 
    for i in range(m):
    	# 选取一个颜色
        markIndex = int(clusters[i])
        # 画点
        plt.plot(data[i, 0], data[i, 1], mark[markIndex])

    mark = ['^b', '^g', '^k', '^r', '+b', '+g', '+k', '+r'] 
    for i in range(k):
    	# 在图中标出中心点，与聚类中其它点的颜色区分开
        plt.plot(Cpoints[i, 0], Cpoints[i, 1], mark[i])
    
    plt.show()

3.2.6 模型存储

def saveModel(obj, modelname):
    f = open(modelname, 'wb')
    pickle.dump(obj, f, 0)
    f.close()

3.3 模型评估

3.3.1 模型加载

def loadModel(modelname):
    f = open(modelname, 'rb')
    Cpoints = pickle.load(f)
    f.close()

    return Cpoints

3.3.2 使用模型聚类

def fit(Cpoints, data, method='E'):
    k = len(Cpoints)
    m, n = data.shape
    clusters = np.zeros(m)
    
    # 遍历每一个点
    for i in range(m):
        minDist = float("inf")
        minIndex = -1
        # 找到该点距离最近的簇中心点
        for j in range(k):
            dist = tr.distance(Cpoints[j], data[i], method)
            # 更新最近的簇中心点
            if dist < minDist:
                minDist  = dist
                minIndex = j
		# 将该点划分到簇中
        clusters[i] = minIndex
	# 绘制聚类图
    tr.showClusters(data, k, Cpoints, clusters)
	
	# 返回聚类结果
    return clusters

3.3.3 sse计算评估

• 采用sse进行结果评估

def sse(Cpoints, data, clusters):
    m = data.shape[0]
    k = len(Cpoints)
    # 存放不同簇中点到中心点的距离和和点的个数
    sseAr = np.zeros((k, 2))

    for i in range(m):
        dist = tr.distance(Cpoints[int(clusters[i])], data[i])
        # 距离和增加
        sseAr[int(clusters[i])][0] += dist
        # 个数增加
        sseAr[int(clusters[i])][1] += 1

    sse = 0
	
	# 计算均值
    for i in range(k):
        sse += (sseAr[i][0] / sseAr[i][1])

    return sse

4. 结果分析

• 按照8：2的比例将数据随机分成了训练集和测试集
• 聚类中与周围不同颜色的点为聚类中心点

4.1 训练结果

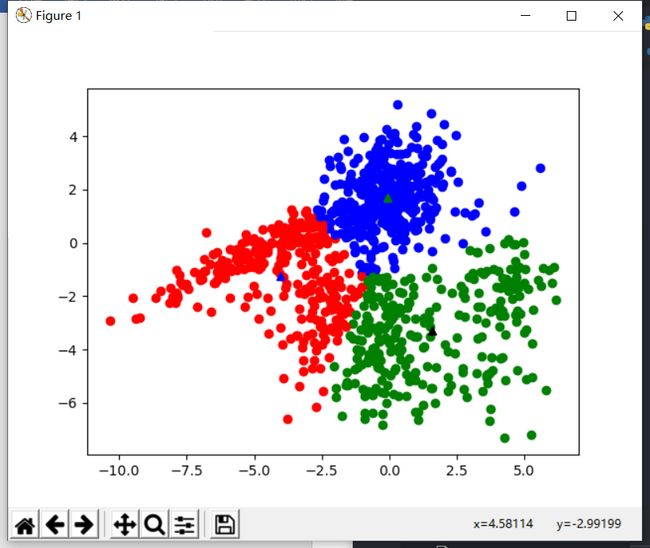
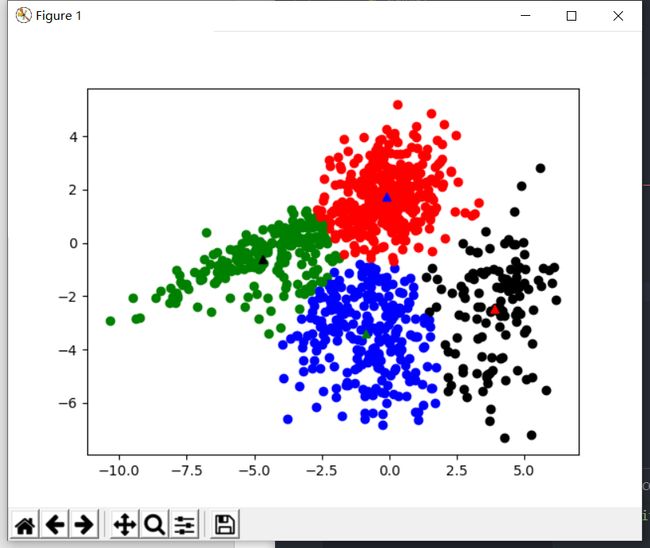
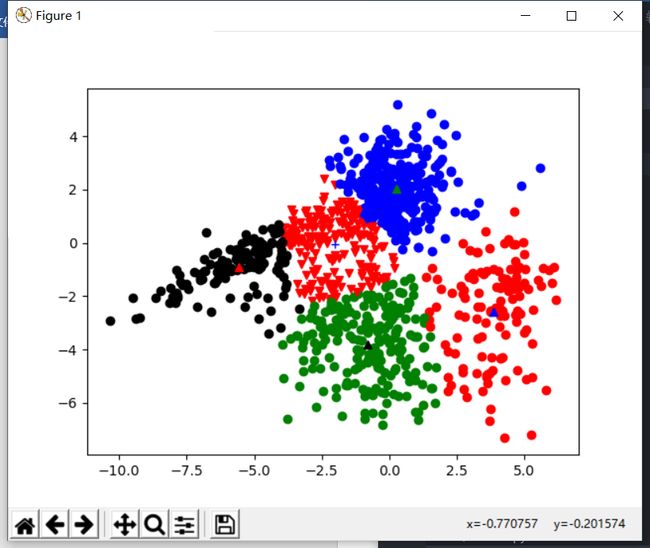
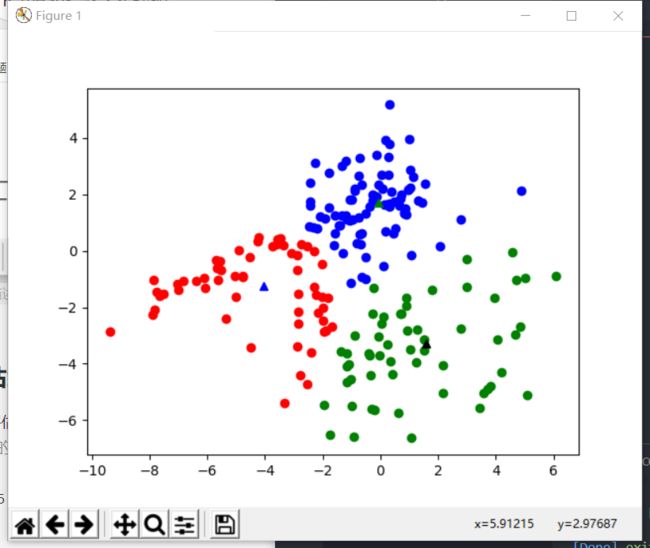
基于欧式距离分类

• 可以看到，当k值增长到5时，聚类效果明显不佳

k = 3	k = 4	k = 5

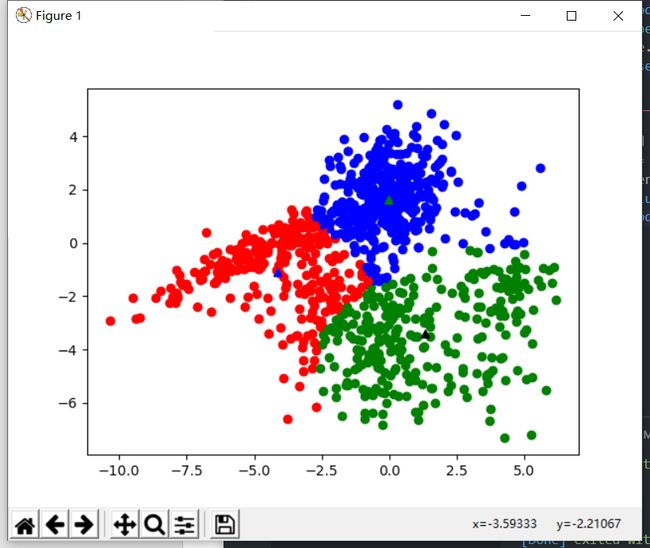
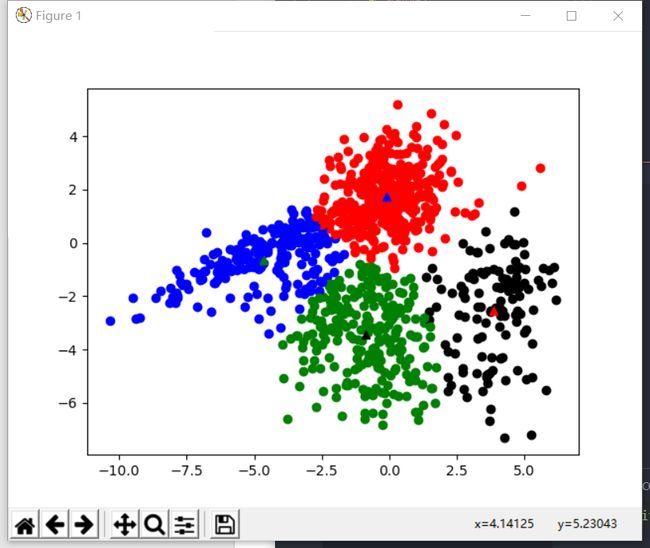
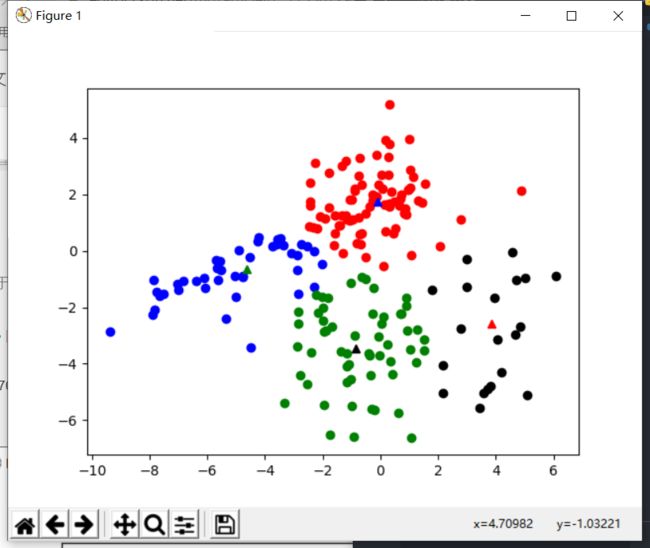
基于曼哈顿距离分类

• 可以看到基于曼哈顿距离分类结果与基于欧氏距离分类结果基本一致

k = 3	k = 4

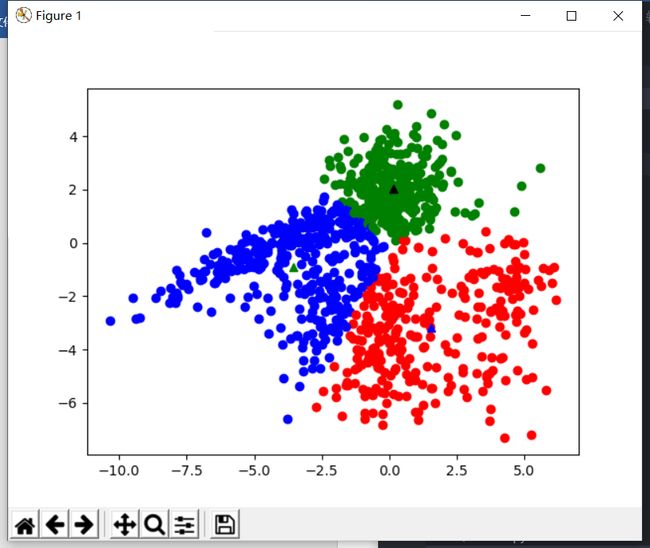
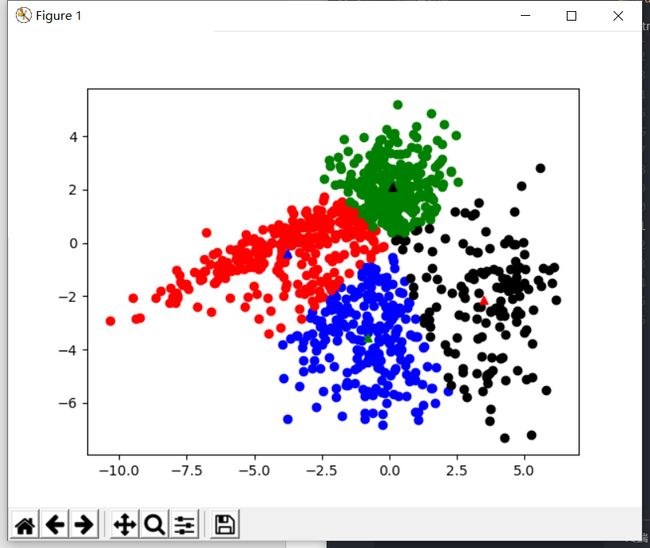
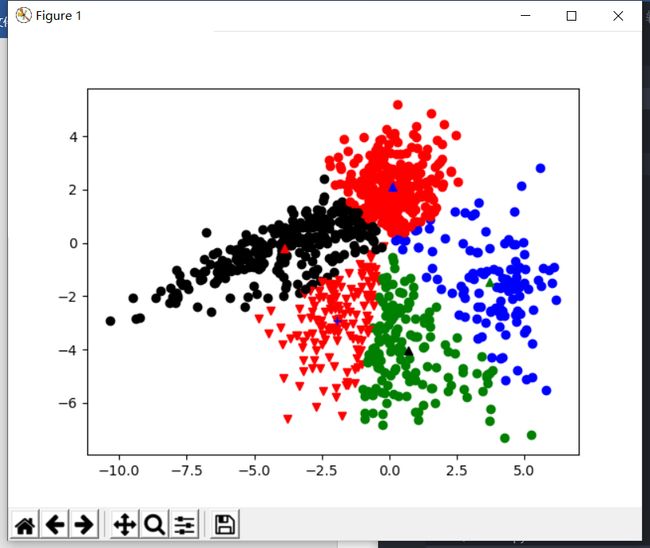
基于余弦距离进行分类

• 可以看到，基于余弦距离的分类在k=5下也有着不错的分类效果，但具体情况需要进行预测评估

k = 3	k = 4	k = 5

4.2 评估结果

• 采用sse进行评估

基于欧式距离的分类评估

• 可以看到基于欧式距离分类，k = 3时为理论上最优k值

k = 3	k = 4	k = 5
6.1702	7.1997	7.6863

基于曼哈顿距离的分类评估

• 结果与欧式距离近似

k = 3	k = 4
6.1370	7.1116

基于余弦距离的分类评估

• 同样是k = 3时最佳

k = 3	k = 4	k = 5
6.1005	7.4509	8.5941

4.3 总结

  在此数据集上，无论是基于欧式距离、曼哈顿距离还是余弦距离，均在k = 3时有着最好的表现，理论上能解释数据最好的k值应该是3。