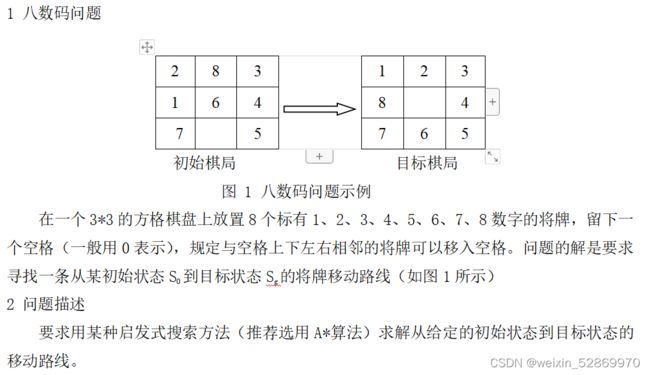
使用Astar(A星)算法解决八数码问题(Python代码)
使用Astar(A星)算法解决八数码问题(附Python代码)
参考文章:A星算法详解(个人认为最详细,最通俗易懂的一个版本)
A*算法作为一种最佳图搜索算法,据说被用于游戏红色警戒的寻路算法。

八数码问题的重述:
Astar算法概述
Astar算法本质上是一种图搜索算法。图搜索算法就是将问题空间看作一个有向图空间,这个图空间由一个个图节点构成,问题的求解就转化为在问题空间中从初始节点出发,寻找一条通向目标节点的路径。在八数码问题中,棋局的每一个不同的状态都是一个节点,节点之间的转换是通过移动空格实现的。这样,通过选定初始节点和确定图转换规则(本问题中就是移动空格),我们就可以生成一个状态图,如:
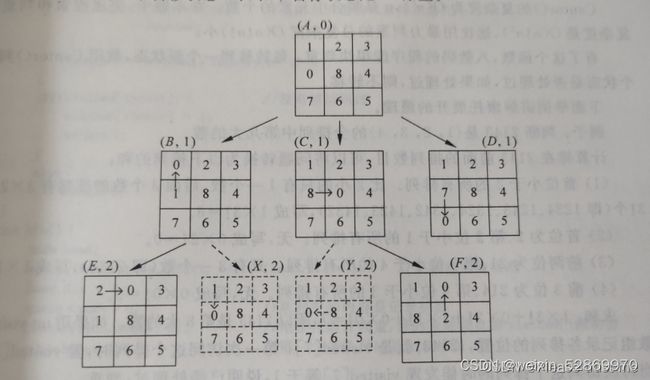
既然问题已经转化为图搜索问题了,那么我们可以确定一下搜索策略了。Astar算法其实和广度优先搜索很像,它与后者不同的地方就是Astar是一种启发式(heuristic)搜索。关于启发式搜索,简单来说就是在每次广搜选择节点时,从中选出一个最有希望出现在最佳路径上的点进行拓展。
在Astar算法中,我们用一个估价函数f(x)评价节点x距离最优解的距离,f(x) = g(x) + h(x)。
其中g(x)为代价函数,用来评价从初始节点到节点x的已付出的搜索代价(通常由搜索步数决定),g(x)越小代表节点x距离初始节点距离越小,提高了搜索的完备性(鼓励机器去尝试不同路径);而h(x)启发函数用来评价节点x距离目标节点的距离,h(x)越小代表节点x距离目标节点距离越小,提高了搜索的效率(鼓励机器去更快接近目标)。
Astar算法额外要求对所有的节点x均有h(x) <= h*(x),这里h*(x)是从节点x到目标节点的最小启发函数值。这句话理解起来有点困难,笔者在此谈一下自己的看法,有不足处欢迎在评论区指出,欢迎讨论。
我的理解是:要找一个最适合描述当前节点到目标节点距离的h(x)函数。
如在八数码问题中,空格只能横向、纵向移动,那么这个h(x)可以是曼哈顿距离。同理,在若在直角坐标系中,这个距离可描述为欧几里得距离。
算法的实现过程如下:
◆ 把起点加入 open list 。
◆ 重复如下过程:
◆ 遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
◆ 把这个节点移到 close list 。
◆ 对当前方格的 8 个相邻方格的每一个方格?
◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
◆ 停止,当你把终点加入到了 open list 中,此时路径已经找到了,或者
◆ 查找终点失败,并且 open list 是空的,此时没有路径。
◆ 保存路径。从终点开始,每个方格沿着父节点移动直至起点,这就是你的路径。
最后附上代码,如果有错拜托评论区指出,转载请注明出处,感谢
import numpy as np
# 定义open表与close表
open_list = []
close_list = []
start_state = np.zeros((3, 3), dtype=int)
target_state = np.zeros((3, 3), dtype=int)
# 定义节点类
class Node:
G = 0
H = 0
F = 0
state = np.zeros((3, 3), dtype=int)
parent = []
# 找num在state状态中的位置x,y
def find_pos(self, state, num):
for i in range(len(state)):
for j in range(len(state[i])):
if state[i][j] == num:
return i, j
def __init__(self, state, prt=[]):
self.state = state
if prt:
self.parent = prt
self.G = prt.G + 1
for i in range(len(state)):
for j in range(len(state[i])):
x, y = self.find_pos(target_state, state[i][j])
self.H = self.H + abs(x - i) + abs(y - j)
self.F = self.G * 1 + self.H * 10
def moveto(self, x, y):
x0, y0 = self.find_pos(self.state, 0)
# new_state = self.state 是错的
newstate = (self.state).copy()
tmp = newstate[x0][y0]
newstate[x0][y0] = newstate[x][y]
newstate[x][y] = tmp
return newstate
# 得到逆序数,用于判断解的存在性
def get_reverse_num(state):
ans = 0
s = ""
for i in range(len(state)):
for j in range(len(state[i])):
# 0即空格,不在考虑范围内
if not state[i][j] == 0:
s += str(state[i][j])
for i in range(len(s)):
for j in range(i):
if s[j] > s[i]:
ans += 1
return ans
# 输出状态及深度
def display(cur_node):
alist = []
tmp = cur_node
while tmp:
alist.append(tmp)
tmp = tmp.parent
alist.reverse()
for node in alist:
print("搜索深度%d" % node.G)
print(node.state)
print()
# 检查state状态是否在list中(可能是open或close表)
def is_in_list(alist, state):
for stat in alist:
if (stat.state == state).all():
return stat
return -1
# 排序的权值函数
def delta(node):
return node.F
# # 输入初始与目标状态
# for i in range(len(start_state)):
# for j in range(len(start_state[i])):
# start_state[i][j] = input("start_state"+"("+str(i+1)+","+str(j+1)+"):")
#
# print("the start state is:")
# print(start_state)
#
# for i in range(len(target_state)):
# for j in range(len(target_state)):
# target_state[i][j] = input("target_state"+"("+str(i+1)+","+str(j+1)+"):")
#
# print("the target state is:")
# print(target_state)
# 调试
start_state = np.array([[2, 8, 3],
[1, 6, 4],
[7, 0, 5]])
target_state = np.array([[1, 2, 3],
[8, 0, 4],
[7, 6, 5]])
# 可行解判断
if get_reverse_num(target_state) % 2 != get_reverse_num(start_state) % 2:
print(get_reverse_num(target_state))
print(get_reverse_num(start_state))
print("找不到可行解!")
exit(-1)
# 可行解存在时,开始启发搜索
open_list.append(Node(start_state))
while open_list:
current_node = open_list.pop(0)
close_list.append(current_node)
# 当open表中取出的恰好为目标状态时
if (current_node.state == target_state).all():
print("可行解已找到!")
display(current_node)
exit(0)
# 否则对当前节点进行拓展
x, y = current_node.find_pos(current_node.state, 0)
for [x_, y_] in [[x+1, y], [x-1, y], [x, y+1], [x, y-1]]:
if 0 <= x_ < len(start_state) and 0 <= y_ < len(start_state):
new_state = current_node.moveto(x_, y_)
# 判断新状态是否在close表
if is_in_list(close_list, new_state) == -1:
# 如果不在close表
if is_in_list(open_list, new_state) == -1:
# 如果也不在open表
open_list.append(Node(new_state, current_node))
else:
# 如果open表中已存在这种状态,则选取G值较小的
index = is_in_list(open_list, new_state)
if current_node.G + 1 < open_list[index].G:
# 如果新路线更好,则放弃旧路线而选择新路线
open_list.pop(index)
open_list.append(Node(new_state, current_node))
# 否则忽略
# 对open表按F值从小到大进行排序
open_list.sort(key=delta)
# bug1:if current_node.state == target_state:
# ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
# bug2:start state与new state同步变化
# def moveto(self, x, y):
# x0, y0 = self.find_pos(self.state, 0)
# new_state = self.state
# tmp = new_state[x0][y0]
# new_state[x0][y0] = new_state[x][y]
# new_state[x][y] = tmp
# return new_state