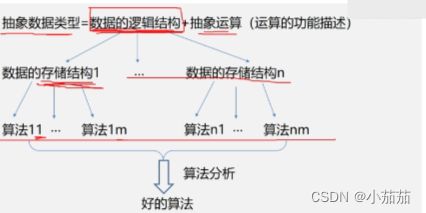
【数据结构】 绪论

1.1 数据结构的研究内容

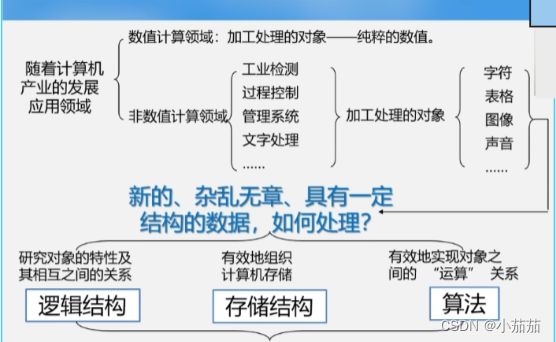
随着计算机应用领域的扩展，计算机越来越多地用于非数值的计算。

1.1.1 线性关系

如：对一个表格的内容进行增删查改

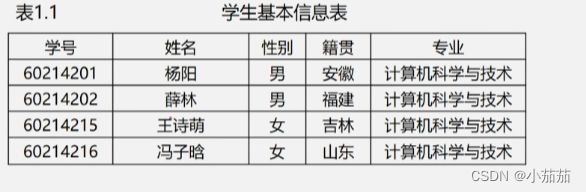
• 操作对象：每位学生的信息（学号、姓名、性别、籍贯、专业等）。

• 操作算法：查询、插入、修改、删除等。

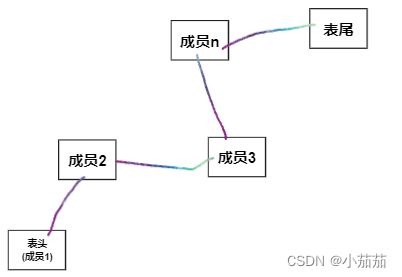
• 操作对象之间的关系：除了开头行和结尾行的操作对象，其余操作对象的行前后都有其他操作对象，操作对象就像被一根绳子串起来的关系称为 线性关系。
  

• 数据结构：线性数据结构、这样一个表格就称为（线性表）。

1.1.2 非线性关系

操作对象之间并不是一个串着一个，操作对象后面不再是一个跟着一个对象，可能是跟着多个对象

如：

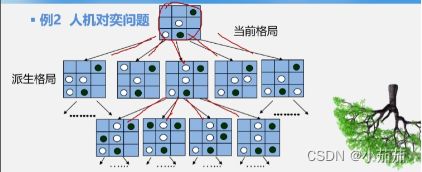
树形结构

• 操作对象：各种棋局的状态，即描述棋盘的格局信息。
• 操作算法：走棋，即选择一种策略是棋局状态发生变化，（由一个格局派生出另一个格局）。
• 操作对象之间的关系：非线性关系、树

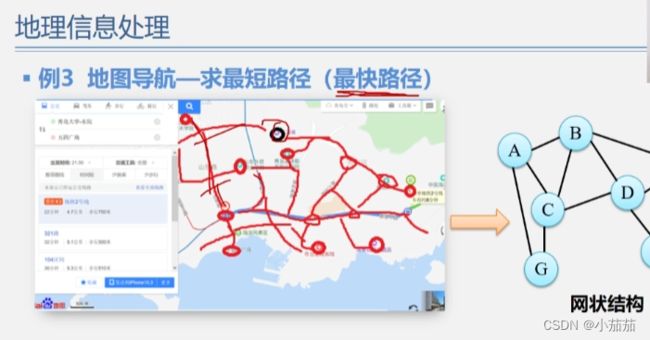
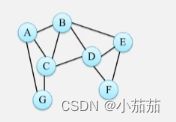
网状结构

由线和点构成的一个结构，操作对象像一张网一样互相连接在一起。

如

操作：找一条最短路径
操作对象：ABCD这些个路线点。
操作关系：网状关系

综上所述

• 这些问题的共同点是无法用数学的公式或程序来描述，而是一些非数值计算的程序设计问题。
• 秒数非数值计算问题的数学模型不再是数学方程，而是如：表、数、图之类的具有逻辑关系的数据。
• 数据结构：研究非数值计算的程序设计中计算机的操作对象以及他们之间的关系和操作的学科。

1.2 基本概念和术语

1.2.1 数据、数据元素、数据项和数据对象

数据：

• 能输入计算机且能被计算机处理的各种符号的集合

  • 信息的载体
  • 对客观事物符号化的表示
  • 能够被计算机识别、存储和加工

• 包括：

  • 数值型的数据：整数、实数等。
  • 非数值型的数据：文字、图像、图形、声音等。

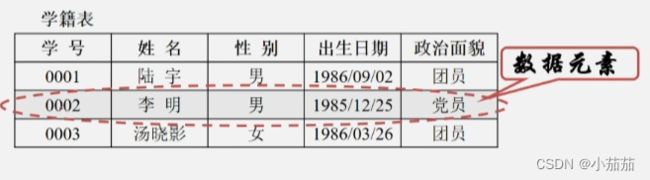
数据元素：

• 组成数据的基本单位，在计算机程序中通常作为一个整体来进行考虑和处理。
• 也简称为元素，或称为记录、结点或顶点。
• 一个数据元可由若干个数据项组成。

比如说这样一个学生表，假设某个同学转学了，那么是对那个同学的那一行进行整体的删除，这样一个学生的相关信息就是作为整个数据的某一个整体来操作 ，每一行学生信息就是组成数据的数据元素

数据项：

• 构成数据元素的最小单位。
  
  比如这张学籍表，数据项就是对应学生的行列所代表的信息，
• 数据、数据元素、数据项的关系。
  • 数据 > 数据元素 > 数据项：
  • 数据是由数据元素组成的，数据元素是由数据项组成的。

数据对象：

• 是性质相同的数据元素的集合，是数据的一个子集
  例如：
  • 整数数据对象的集合是 N = {0，±1，±2…}
  • 字母字符数据对象是集合C = {‘A’,‘B’…‘Z’}
  • 学籍表也能看成一个数据对象，由若干条学生记录构成的子集。

数据元素与数据对象

• 数据元素——组成数据的基本单位
  • 与数据的关系：是集合的个体。
• 数据对象——性质相同的数据元素的集合
  • 与数据的关系：集合的子集

1.2.2 数据结构

数据结构：

• 数据元素相互之间的关系称为结构（比如：线性、非线性）。
• 相互之间存在一种或多种特定关系的数据元素的集合。
• 数据结构时带结构的数据元素的集合

数据结构包括：

1. 逻辑结构：数据元素之间的逻辑关系关系，称为逻辑结构。
2. 物理结构（存储结构）：数据元素及其关系在计算机内存中的表示（也称为映像）。
3. 数据的运算和实现，即对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现。

逻辑结构：

• 数据元素之间的逻辑关系。
• 和数据的存储无关。
• 从具体的问题抽象出来的数学模型。

物理结构（存储结构）：

• 数据元素及其关系在内存中存储的结构（存储方式）
• 是数据结构在计算机中的表示。

逻辑结构与存储结构的关系：

• 存储结构时逻辑关系的映像和元素本身的映像。
• 逻辑结构时数据结构的抽象，存储结构时数据结构的实现。

逻辑结构的种类

划分方法1：

• 线性结构

  • 有且仅有一个开始和一个终端结点，并且所有结点都最多只有一开直接前趋和一个直接后继。
  • 如：线性表、栈、队列、串
  • 每个结点成员最多前后各有一个成员
    

• 非线性结构

  • 一个结点可能有多个直接前趋和直接后继。
  • 如：数、图
  • 每个结点成员都可能连接着多个其他结点成员。
    

划分方法2：

• 集合结构：结构中的数据元素之间处理同属于一个集合的关系之外，没有其他任何的关系。

• 线性结构：结构中的数据元素之间存在着一对一的线性关系。

• 树形结构：结构中的数据元素之前存在着一对多的层次关系

• 图状结构或网状结构：结构中的数据元素之间存在着多对多的任意关系。

存储结构的种类

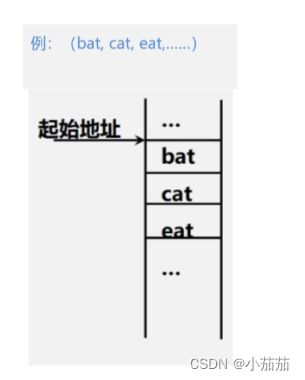
1. 顺序存储结构

   • 按着一定的顺序依次存储数据元素，数据元素之间的逻辑关系由元素的存储位置表示。
   • C语言中用数据来实现顺序存储结构。
   • 例如要存这样一组字符串，就用字符串数组，往内存中存就是按照起始地址，以及数组元素类型大小往后存储

2. 链式存储结构

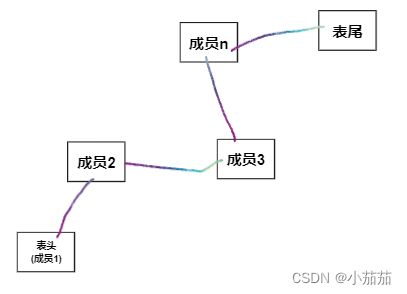
   • 用一组任意的存储单元存储数据元素，数据元素之间的逻辑关系用指针来表示。
   • C语言中用指针来实现链式存储结构。
   • 存储着每个元素本身的同时，还存储着下一个元素的地址。

像有根链条连起来一样，前一个元素存着下一个元素的地址，不管你存在哪里，等用到你的时候都可以用前一个元素存着的下个元素的地址找到下一个元素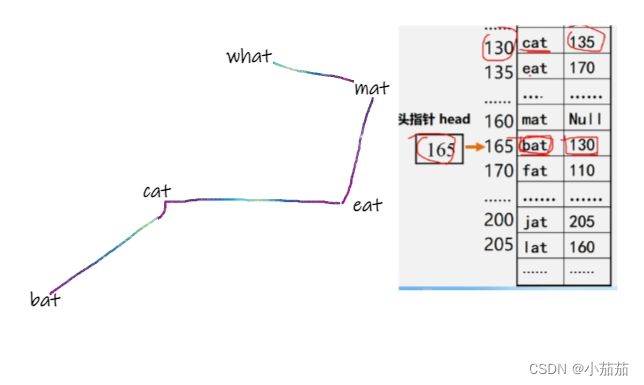

3. 索引存储结构

   • 存储结点信息的同时，还建立附加的索引表。

   • 存储真正的信息的同时还建立了个索引表（目录），方便查找

4. 散列存储结构

1.2.3 数据类型和抽象数据类型

数据类型：

一组性质相同的值得集合，以及定义于这个值集合上的一组操作的总称

• 内置类型：int、double、char这些。

• 自定义类型：数组、enum、struct、union这些。

• 还有指针、void类型的指针。

• 数据类型的作用

  • 约束变量或常量的取值范围
  • 约束变量或常量的操作

抽象数据类型（ADT）

一个数学模型以及定义在刺数学模型上的一组操作。

• 抽象数据类型

  • 由用户定义，从问题抽象出数据模型（逻辑结构）。
  • 还包括定义在数据模型上的一组抽象运算（相关操作）。
  • -不考虑计算机内的具体存储结构与运算的具体实现算法。

• 抽象数据类型的形式定义

一个抽象数据类型的定义格式如下：

其中：
数据对象数据关系的定义用伪代码描述。

基本操作的定义格式

• 基本操作名（参数表）——函数
  • 参数表：赋值参数，只为操作提供输入值（传值调用）。
  • 引用参数以 & 开头，除可提供输入值外，还可返回操作结果（传址调用）。
• 初始条件：（初始条件描述）
  • 描述操作执行之前数据结构和参数应满足的条件。
  • 若不满足，则操作失败，并返回相应出错信息。若初始条件为空，则省略之（类似if ）
• 操作结果：（操作结果描述）
  • 作正常完成之后，数据结构的变化状况和应该返回的结果。

1.3 抽象数据类型的表示与实现

定义一个圆

注：这是个伪代码，要实现得转成各类语言对应格式。

C语言实现抽象数据类型

• 用已有数据类型定义描述它的存储结构
• 用函数定义描述它的操作。

简单用代码弄一下

#include 
#include 
void Circle(int* C,int r,int x,int y)//数据对象
{
        C[0]= r;
        C[1]= x;
        C[2]= y;
}
double Area(int* C)
{
        return 3.14 * pow(C[0],2);
}
double Circumference(int* C)
{
        return 2 * 3.14 * C[0];
}
int main()
{
        int C[3]= {0},r,x,y;
        int i;
        printf("请输圆的半径及xy的坐标");
        scanf ("%d %d %d",&r,&x,&y);

        Circle(C,r,x,y);
        printf("圆的面积是：%lf\n",Area(C));
        printf("圆的周长是：%lf\n",Circumference(C));
        return 0;
}

请输圆的半径及xy的坐标 3 3 3
圆的面积是：28.260000
圆的周长是：18.840000

1.4 算法和算法分析

1.4.1 算法和算法分析1

算法的定义

对特定问题求解方法和步骤的一种描述，它是指令的有限序列。其中每个指令表示一个或多个操作。

算法的描述

描述代码该怎样实现

例如：描述怎么实现求一元二次方程的根

1. 文字描述：英语、中文 -
   • 如
     
2. 流程图：传统流程图、NS流程图
   
3. 伪代码：类语言：类C语言
4. 程序代码：C语言程序、JAVA语言程序

算法与程序

• 算法：是解决问题的一种方法或一个过程，考虑如何将输入转换成输出，一个问题可以有多种算法。
• 程序：是用某种程序设计语言对算法的具体实现。
  

算法特性

1. 有穷性：一个算法必须总是在执行有穷步之后结束，且每一步都在有穷时间内完成。
2. 确定性：算法中的每一条指令必须有确切的含义，没有二义性，在任何条件下，只有唯一的一条执行路径，即对于相同的属兔只能得到相同的输出。
3. 可行性：算法是可执行的，算法描述的操作可以通过已经实现的基本操作执行有限次来实现。
4. 输入：一个算法有零个输入或多个输入，算法可以没有输入
5. 输出：必须要有一个或多个输出，算法必须要有输出。

算法设计的要求

1. 正确性
   

2. 可读性

   

3. 健壮性

   

4. 高效性
   

1.4.2 算法和算法分析2

算法效率

1. 时间效率：指的是算法所耗费的时间
2. 空间效率：指的是算法执行过程中所耗费的存储空间

算法时间效率的度量

算法时间效率可以用依据改算法编制的程序在计算机上执行所消耗的时间来度量。

两种度量方法：

• 事后统计
  • 根据算法，先编好程序，编好程序之后实际运行一下程序，看看花了多少时间。
  • 缺点：编写程序实现算法将花费较多的时间和精力，所得结果依赖于计算机的软硬件等环境因素，掩盖算法本身的优劣。
• 事前分析
  • 对算法所消耗资源的一种估算方法。
  • 更多的时候使用这个方法。

事前分析方法

• 一个算法的运行时间时指一个算法在计算机上运行所耗费的时间，大致可以等于计算机执行一种简单的操作（赋值、比较、移动等）所需的时间与算法中进行的简单操作次数乘积。
  • 算法运行时间 = 一个简单操作所需要的时间 * 简单操作次数
• 也就是算法中每条语句的执行时间之和
  • 算法运行时间 = ∑ 每条语句的执行次数 * 该语句执行一次所需的时间
  • 每条语句执行一次所需要的时间，一般是随机器而异的，和算法本身无法。

例如：

• 两个 n * n矩阵相乘的算法可描述为：

for(i = 1;i <= n;i++)//执行n + 1次
{
		for(j = 1;j <= n;j++)//执行n(n + 1)次
		{
				c[i][j] = 0;//n * n次
				for(k = 0;k < nk++)//执行n * n(n +1)次
				{
						c[i][j] = c[i][j]+a[i][k] * b[k][j];//n * n * n次
				}
		}	
}

- 所有语句的执行次数加起来就是时间频度之和。
- 把算法所耗费的时间定义为**该算法中每条语句的频度之和**。
-则上述算法的时间消耗为T(n)为：T(n) = 2n ^ 3 + 3n ^ 2 + 2n + 1（这种方法很麻烦）

算法时间复杂度的渐进表示法

• 为了方便比较不同算法的时间效率，我们仅比较他们的数量级

  例如：两个不同的算法，时间消耗分别是：

  • T1(n) = 10n ^ 2 与 T2(n) = 5n ^ 3 —— 数量级（次方）越大的越不好。

• 若有若干辅助函数 f(n)，使得 n 趋近于无穷大，T(n) / f(n)的极限值为不等于零的常数，则称 f(n) 是 T(n)的同数量级函数（同阶，次方相同）。记作**T(n) = O(f(n)),称O(f(n))为算法的渐进时间复杂度**(O是数量级的符号)，简称时间复杂度。

• 一般情况下，不必计算所有操作的执行次数，而只考虑算法中的基本操作执行的次数，它是问题规模n的某个函数，用T(n)表示

• 直接抓大头，常数去掉，只取次方最大项，算法中的大哥就是执行次数最多的语句，把它抓出来
  

算法中基本语句重复执行的次数是 问题规模n的某个函数f(n),算法的时间量度记作：T(n) = O(f(n))

• 它表示随着 n 的增大，算法执行的时间的增长率和 f(n) 的增长率相同，称为渐进时间复杂度

基本语句重复执行的次数

• 算法中重复执行次数和算法的执行时间成正比的语句。
• 对算法运行时间贡献最大。
• 执行次数最多的语句（一般为嵌套最内层的语句）.

问题规模

n越大算法的执行时间就越长

• 排序：n为记录数。
• 矩阵：n为矩阵的阶数（次方）。
• 多项式：n为多项式的项数（老大是最高次项，且系数可以去掉）。
• 集合：n为元素个数。
• 数：n为树的结点个数。
• 图：n为图的顶点数或边数。

1.4.3 算法和算法分析3

分析算法时间复杂度的基本方法

1. 找出语句频度最大（执行次数最多）的那条语句作为基本语句。
2. 计算基本语句的频度（执行多少次）得到问题规模 n 的某个函数f(n)。
3. 取其数量级用符号 “O” 表示，（ f(n) 抓大头，并且去掉大头的系数，剩下的就是数量级）

举个栗子：

int x = 0,y = 0;//执行1次
        for(int k = 0;k < n;k++)//这条for语句执行n + 1次
        {
                x++ ;//这个循环体执行n次
        }

        for(int i = 0;i < n;i++)//执行n + 1次
        {
                for(int j = 0;j < n;j++)//外层循环每执行1次这个for循环就要执行n + 1次
                                        //所以这个for循环要执行 n * (n + 1)次
                y++ ;//执行n * n 次
        }

• 所以这段代码执行次数最多的是函数 f(n) = n * (n + 1) 次。
• 抓大头之后，这段代码的数量级就是n ^ 2，时间复杂度就是T(n) = O (n ^ 2) 。-

void exam(float x[][],int m,int n)
{
        float sum[];
        for(int i = 0;i < m;i++)
        {
                sum[i] = 0.0 ;
                for(int j = 0;j < n;j++)
                {
                        sum[i] += x[i][j];//这条语句嵌套最深，所以复杂度最高，执行m * n 次
                                        //表示成函数就是f(n) = m * n,数量级为T(n) = O(m * n)
                }
        }
        for(i = 0;i < m;i++)
        {
                cout << i << ":"<< sum [i]<< endl;
        }
}

算法时间复杂度例题

1. N * N 矩阵相乘

        for(i = 1;i <= n;i++)
        {
                for(j = 1;j <= n;j++)
                {
                        c[i][j] = 0;
                        for(k = 1;k <= n;k++)
                        {
                                c[i][j] = c[i][j] + a[i][k] * b[k][j];//这条语句执行最多
                                //f(n) = n * n * n,T(n) = O(n^3)
                        }
                }
        }

f(n) = n * n * n ，时间复杂度 T(n) = O(n^3)

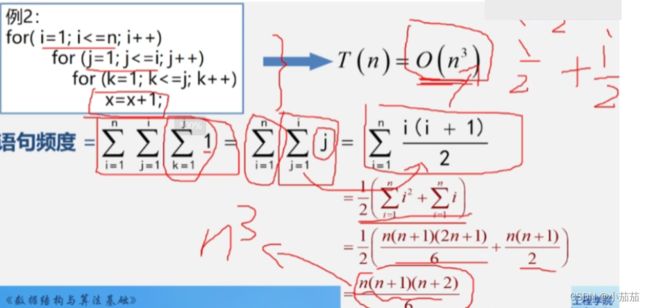
      for(i = 1;i <= n;i++)
        {
                for(j = 1;j <= i;j++)
                {       
                        for(k = 1;k <= j;k++)
                        {
                                x = x + 1;//T(n) = O(n^3)
                        }
                }
        }     

第二重是j到i，j是变量，相当于1+2+3+…+i等于i*（i+1）/2,第一层同理。

3. 分析以下程序段的时间复杂度
   

• 第一步：
  • 找执行次数最多的语句（i = i * 2）
• 第二步：找函数f(n)
  • 若循环执行1次：i = 1 * 2 = 2
  • 若循环执行2次：i = 2 * 2 = 2^2
  • 若循环执行3次：i = 2 * 2 * 2 = 2^3…
  • 若循环执行x次：i = 2^x
  • 设语句 ② 执行次数为x次，由循环条件 i <= n可知，2^x <= n —>x <=log₂n
  • 可以得出函数的方程为f(n) <= log₂n
• 第三步：取数量级
  • 取最大值f(n) <= log₂n
  • 所以该程序段的时间复杂度为T(n) = O(log₂n)

1.4.4 算法和算法分析4

算法时间复杂度计算

有的情况下，算法中基本操作重复执行的次数还随问题的输入数据集不同而不同

【例】顺序查找，在数组a[i]中查找值等于 e 的元素，返回其所在位置。

for(i = 0;i < n;i++)
{
		if(e == a[i])
		{
				return i + 1;
				//找到，则返回是第几个元素
        }
}
return 0;

最好的情况是第一个元素就是要查找的元素，最坏则是最后一个元素，循环体执行的次数和 e 实际放的位置有关

最好情况：执行 1 次
最坏情况：执行 n 次
平均时间复杂度：O(n)

算法时间复杂度

• 最坏时间复杂度：指在最坏情况下，算法的时间复杂度。
• 平均时间复杂度：指在所有输入实例在等概率出现的情况下，算法的期望运行时间。
• 最好时间复杂度：指在最好情况下，算法的时间复杂度计算。

一般总是在考虑最坏情况下的时间复杂度，以保证算法的运行时间不会比它更长。

对于复杂的算法，可以将它分成几个容易估算的部分，然后用大O加法法则和乘法法则，计算算法的时间复杂度。

• 加法法则
  • T(n) = T1(n) +T2(n) = O(f(n)) + O(g(n)) = O(max(f(n),g(n)))
  • 如果函数 T 可以分成两个函数来计算，可以分别来求解这两个函数的数量级，然后求这两个函数数量级里的最大值，就是整个 T(n) 函数的数量级。
• 乘法法则
  • T(n) = T1(n) * T2(n) = O(f(n)) * O(g(n)) = O(f(n) * g(n))
  • 如果函数 T(n) 可以分解成两个函数的乘积，分别求这两个稍微简单点的函数的数量级，T(n) 函数的数量级就是这两个函数的数量级相乘

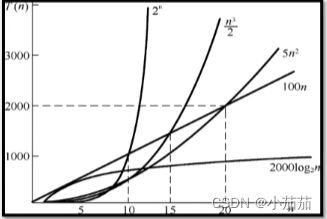
算法时间效率的比较

当 n 取得很大时，指数时间算法和多项式时间算法在所需时间上非常悬殊。

• 指数时间算法

• 多项式时间算法（线性）

  

时间复杂度 T(n) 按数量级递增顺序为：

设计算法的时候就要考虑，尽量设计复杂度低的

渐进空间复杂度

空间复杂度：算法所需存储空间的度量。

• 记作：S(n) = O(f(n))
• 其中 n 为问题的规模（或大小）

算法要占据的空间

• 算法本身要占据的空间，输入/输出，指令，常数，变量等
• 算法要使用辅助空间

【例】将一维数组 a 中的n个数逆序放到原数组中

算法1的空间效率高于算法2的空间效率

 		int n,i,a[10] = {1,2,3,4,5,6,7,8,9,10};
        int sz = sizeof(a)/sizeof(a[0]);

        printf("你要逆序几个数：");
        scanf ("%d",&n);

        for(i = 0;i < n;i++)
        {
                int t = a[i];
                a[i] = a[sz -1-i];
                a[sz -1- i] = t;
        }
        for(i = 0;i < sz;i++)
        {
                printf("%d ",a[i]);
        }
        putchar('\n');

设计好算法的过程