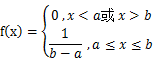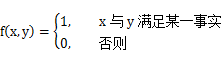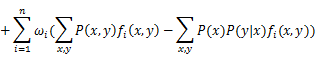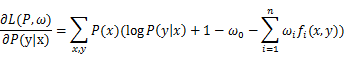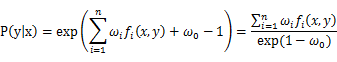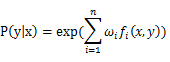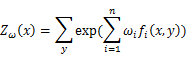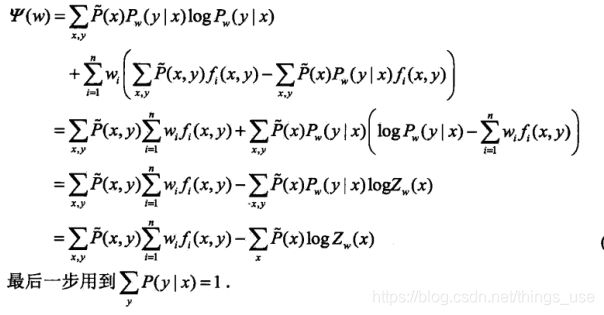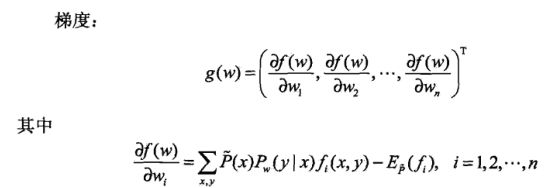机器学习-最大熵模型

        最大熵模型是一种分类模型，它学习之后对某个x判断的结果是一个概率，即对一个自变量，它的分类分别是y1,y2,y3…yn的概率，然后概率最大的分类结果就是我们所要的结果分类ym。

1. 最大熵原理

        最大熵原理认为，学习概率模型时在所有可能的概率模型中，熵最大的模型是最好的模型，这个是准则。但是在学习过程中，往往是有约束条件的，所以，熵最大原理也可以表述为在满足约束条件的模型集合中选取上最大的模型。

根据以前的知识，我们知道熵的定义为：

                                                       

其中熵满足下列不等式：

                                                       

其中|X|是X的取值的个数（不等式怎么来的，先不考虑，应该有严格的数学证明）。通过上面不等式，我们可以得出熵最大的情况就是H(P) = log|X|，而什么情况下可以满足等式呢，就是当X的分布是均匀分布时，等式成立，也就是熵最大，下面进行简单的说明：

先给出均匀分布：

                                                         

不考虑等于0的情况，均匀分布就是等可能，即p(x)=1/(b-a)带入不等式中的两个式子的H(p)=log(b-a)，log|X|=log(b-a)，所以H(p)=log|X|，所以这里得出的结论是：在所有的X即不确定的部分是等可能的情况下，熵是最大的。

上述模型只是原理性的东西，是我们希望得到的最理想的结果，但是实际上模型都是有限制条件的，而加上限制条件后才是我们实际应用中更常遇到的。而我们的目标是在限制条件下，让其熵尽可能的大，从而尽可能的得到更好的模型。

2.最大熵模型的定义

        定义的目的是在给定条件下，使熵最大化，所以我们首先要确定对应的条件。

        在给定的训练数据中，我们可以确定的是联合概率分布P(X,Y)的经验分布和边缘分布P(X)，具体的计算方法是用对应的出现的频次除以训练数据的样本容量N。

        对于分类模型我们可以归结为“是”与“否”，所以我们可以用1表示输入的x和y满足某一事实，即在特征x的情况下是分类y，0表示不满足，其用特征函数表示如下：

                                           

        特征函数f(x,y)关于经验分布P(x,y)的期望用E1(f)表示：

                                         

        上面的联合概率是我们可以直接得到的，而我们要求的是条件概率p(y|x)，根据条件概率公式，我们可以得到p(x,y)=p(y|x)p(x)，所以特征函数f(x,y)管与模型p(y|x)与经验分布p(x)的期望用E2(f)表示：

                                  

       进一步我们希望这两个期望相等的即E1(f)=E2(f)，也就是：

                               

还有一个条件就是：

                                    

在条件x下所有分类的概率和是1，这个是没有疑问的。

为什么是两个等式条件，因为两个等式条件可以在最优化问题中确定唯一值。

下面就是定义在条件概率分布P(Y|X)上的条件熵：

                               

这个也就是我们的目标函数，也是我们需要求最优值的函数。

3.最大熵模型的学习

根据上面的分析，我们可以得出，最大熵吗，模型的学习可以形式化为约束最优化的问题：

最大化：

条件：  E1(f)-E2(f)=0

          

按照习惯，我们一般将其转化为求值最小值的问题：

最小化：

条件：  E1(f)-E2(f)=0

          

求解约束条件下的最优化问题，一般用拉格朗日乘子法，引入拉格朗日乘子ω1，ω2，ω3…ωn，定义拉格朗日函数L(P, ω)。

         

通过拉格朗日对偶性将极小极大问题转化为极大极小问题。我们的目标是求，通过拉格朗日乘子法引入拉格朗日乘子，然后通过对偶问题转化为求乘子。

在L(P,ω)中对P(y|x)求偏导得：

        

在p(x)>0的情况下，令偏导等于0，得：

        

对于上式，由于可以取任意值，所以我们一般取1，从而得到:

                     

又由于，得：

                                   

                                   

其中是规范化因子。什么要加上规范化因子，因为对于一个条件下，所有可能y的取值概率和需要是1，而规范化因子，我们可以看到就是所有分子的和。

一路公式到这里，我们就要看到曙光了。只要我们知道了所有的拉格朗日乘子ω，我们就可以求得x下某个分类的概率了，所以下面的任务我们就是需要通过算法求出这些个ω。

4.模型学习的最优化算法

这里我只会拟牛顿法：

上面我们得出了最大熵模型的最终判定公式：

                                    

我们接着看上面的拉格朗日乘子法那个特别长的公式，实际展开后化简得：

过程太长了，我就直接贴个图片了：

这里的P我在上面的一些公式中简写为了P，主要是公式打起来太麻烦了。

为什么这么做，我觉得目的就是要消去P(y|x)这个为止变量。然后带入Zωx得到我们的目标函数：

牛顿法中，我们是要求一阶导数的，即梯度，所以对上面的目标函数求梯度，而未知数是ωi，所以梯度为：

怎么理解上述梯度的表达式，我们将目标函数展开一些，未知数是ω1，ω2，ω3…ωi这些，当对某个ωi求导的时候，其他的ω都可以看作是非未知量，自然就消掉了，从而得出了上面梯度的表达式。接下来就是具体的算法过程了，如果需要更详细读懂下面算法，就需要详细看下牛顿法，拟牛顿法相关的东西：

     

1. 结语

其实到这里，回看一下最大熵模型，目的是求一系列的ω，然后用                 

        这个公式求出一个条件概率，可能是多个，因为对应一个x可能有不同的y的分类，我们取概率最大的那个，所以说这个是个分类模型。

        感觉理论很清晰，但是其具体的应用场景确实不太清楚，不像其他机器学习算法，能明显给你一个结果，是或不是，可能需要以后结合实际应用再深入一步了解应用。