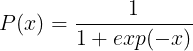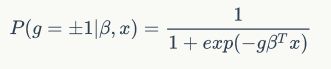机器学习中的损失函数

目录

一、常见的MSE、MAE损失函数

1.1 均方误差、平方损失

1.2 平均绝对误差

二、L1_Loss和L2_Loss

2.1 L1_Loss和L2_Loss的公式

2.2 几个关键的概念

1、鲁棒性（robustness）

2、稳定性

三、smooth L1损失函数

四、Cross entropy损失和Softmax损失

1、Cross entropy

2、Softmax Loss

五、Logistic Loss

---

深度学习里面有很多的损失函数，对于MSE、MAE损失函数可能已经耳熟能详了了，对于L1、L2正则化也很熟悉，那你知道什么是L1_loss和L2_loss吗，以及在目标检测的系列论文比如fast-RCNN、faster-RCNN中经常出现的smooth L1损失又是什么呢？

一、常见的MSE、MAE损失函数

1.1 均方误差、平方损失

均方误差（MSE）是回归损失函数中最常用的误差，它是预测值与目标值之间差值的平方和，其公式如下所示：

                                                  

下图是均方根误差值的曲线分布，其中最小值为预测值为目标值的位置。我们可以看到随着误差的增加损失函数增加的更为迅猛。

                                     

优点：各点都连续光滑，方便求导，具有较为稳定的解

缺点：不是特别的稳健，为什么？因为当函数的输入值距离中心值较远的时候，使用梯度下降法求解的时候梯度很大，可能导致梯度爆炸

1.2 平均绝对误差

平均绝对误差（MAE）是另一种常用的回归损失函数，它是目标值与预测值之差绝对值的和，表示了预测值的平均误差幅度，而不需要考虑误差的方向（注：平均偏差误差MBE则是考虑的方向的误差，是残差的和），范围是0到∞，其公式如下所示：

                                                                     

                            

优点：无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解

缺点：在中心点是折点，不能求导，不方便求解

备注：上面的两种损失函数也被很多资料或者是教材称之为

L2损失和L1损失，但是本文还是将它们跟下面的L1损失和L2损失进行区分了的。

二、L1_Loss和L2_Loss

2.1 L1_Loss和L2_Loss的公式

L1范数损失函数，也被称为最小绝对值偏差（LAD），最小绝对值误差（LAE）。总的说来，它是把目标值（Yi)与估计值（f(xi))的绝对差值的总和（S)最小化：

                                                  

L2范数损失函数，也被称为最小平方误差（LSE）。总的来说，它是把目标值（Yi)与估计值（f(xi))的差值的平方和（S)最小化：

                                                

L1范数与L2范数作为损失函数的区别能快速地总结如下：

L2损失函数	L1损失函数
不是非常的鲁棒（robust）	鲁棒
稳定解	不稳定解
总是一个解	可能多个解

总结：实际上我们发现，其实所谓的L1_Loss与L2_Loss与前面说的MSE、MAE损失函数一个1/n的区别，所以他们的优点和缺点是互通的。

2.2 几个关键的概念

1、鲁棒性（robustness）

因为与最小平方相比，最小绝对值偏差方法的鲁棒性更好，因此，它在许多场合都有应用。最小绝对值偏差之所以是鲁棒的，是因为它能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果需要考虑任一或全部的异常值，那么最小绝对值偏差是更好的选择。从直观上说，因为L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数来得大，因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小。

2、稳定性

最小绝对值偏差方法的不稳定性意味着，对于数据集的一个小的水平方向的波动，回归线也许会跳跃很大。在一些数据结构（data configurations）上，该方法有许多连续解；但是，对数据集的一个微小移动，就会跳过某个数据结构在一定区域内的许多连续解。在跳过这个区域内的解后，最小绝对值偏差线可能会比之前的线有更大的倾斜。相反地，最小平方法的解是稳定的，因为对于一个数据点的任何微小波动，回归线总是只会发生轻微移动；也就说，回归参数是数据集的连续函数。

三、smooth L1损失函数

其实顾名思义，smooth L1说的是光滑之后的L1，前面说过了L1损失的缺点就是有折点，不光滑，那如何让其变得光滑呢？

smooth L1损失函数为：

                                                

smooth L1损失函数曲线如下图所示，作者这样设置的目的是想让loss对于离群点更加鲁棒，相比于L2损失函数，其对离群点（指的是距离中心较远的点）、异常值（outlier）不敏感，可控制梯度的量级使训练时不容易跑飞。

                                            

smooth L1损失函数曲线。

四、Cross entropy损失和Softmax损失

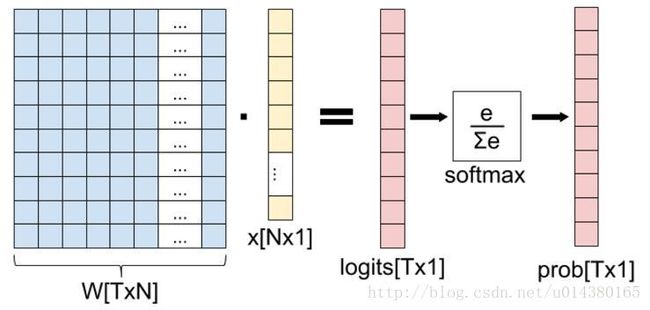
softmax是一个全连接层，功能是将卷积神经网络计算后的多个神经元输出，映射到（0，1）区间，给出每种分类的概率情况。下面主要记录全连接层到损失层是如何计算的。

                             

图的等号左边为全连接，W为权值，x是全连接层的输入（卷积运算激活池化后的特征向量，不一定为N*1,可以为S*P，这里只不过为了便于理解计算，把向量拉直为SP*1，即N*1，N=SP）假设全连接层前面连接的是一个卷积层，这个卷积层的输出是100个特征（也就是我们常说的feature map的channel为100），每个特征的大小是4*4，那么在将这些特征输入给全连接层之前会将这些特征flat成N*1的向量（这个时候N就是100*4*4=1600）。再看W，W是T*N的矩阵，其中N是由输入决定的，T是有网络输出的类别决定的，比如输出为10个类，则T=10.W和x运算后得到一个T*1的向量，向量大小没有限制。下一步就是softmax，softmax作用是将T个输入映射为概率，刚才打比方说有10个类别，则每个输出值就是每种类别的概率，显然概率之和为。分母为所有情况之和，分子为各种单一情况运算。终于转化为概率了，那接下来为了衡量好坏，当然是选择误差函数了，因为是概率输入，当然理所当然使用交叉熵了，

1、Cross entropy

首先理一下熵的概念，现有关于样本集的2个概率分布p和q，其中p为真实分布，q非真实分布。按照真实分布p来衡量识别一个样本的所需要的编码长度的期望(即平均编码长度)为：

                                                                 

如果使用错误分布q来表示来自真实分布p的平均编码长度，则应该是：

                                                               

其中第一个期望为信息熵，反应的是香农信息量的期望，第二个为交叉熵。信息熵代表的是随机变量或整个系统的不确定性，熵越大，随机变量或系统的不确定性就越大。交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。交叉熵越低，这个策略就越好，最低的交叉熵也就是使用了真实分布所计算出来的信息熵，因为此时 ，交叉熵 = 信息熵。这也是为什么在机器学习中的分类算法中，我们总是最小化交叉熵，因为交叉熵越低，就证明由算法所产生的策略最接近最优策略，也间接证明我们算法所算出的非真实分布越接近真实分布。

2、Softmax Loss

                                                                                

首先L是损失。Sj是softmax的输出向量S的第j个值，前面已经介绍过了，表示的是这个样本属于第j个类别的概率。yj前面有个求和符号，j的范围也是1到类别数T，因此y是一个1*T的向量，里面的T个值，而且只有1个值是1，其他T-1个值都是0。那么哪个位置的值是1呢？答案是真实标签对应的位置的那个值是1，其他都是0。所以结果为：

                                                                               

j指向当前样本的真是标签。假设一个5分类问题，然后一个样本I的标签y=[0,0,0,1,0]，也就是说样本I的真实标签是4，假设模型预测的结果概率（softmax的输出）p=[0.2,0.3,0.4,0.6,0.5]，可以看出这个预测是对的，那么对应的损失L=-log(0.6)，也就是当这个样本经过这样的网络参数产生这样的预测p时，它的损失是-log(0.6)。那么假设p=[0.2,0.3,0.4,0.1,0.5]，这个预测结果就很离谱了，因为真实标签是4，而你觉得这个样本是4的概率只有0.1（远不如其他概率高，如果是在测试阶段，那么模型就会预测该样本属于类别5），对应损失L=-log(0.1)。那么假设p=[0.2,0.3,0.4,0.3,0.5]，这个预测结果虽然也错了，但是没有前面那个那么离谱，对应的损失L=-log(0.3)。我们知道log函数在输入小于1的时候是个负数，而且log函数是递增函数，所以-log(0.6) < -log(0.3) < -log(0.1)。简单讲就是你预测错比预测对的损失要大，预测错得离谱比预测错得轻微的损失要大。

五、Logistic Loss

通常，Logistic函数的定义如下：

                                                                     (1)

其中，。其中一个重要的性质为：

                    

                           

公式(1)则是被应用到了Logistic回归中，

                                                                            (2)

其中为响应参数，表示特征向量，此时表示的是样本标签。另一种表示形式将标签与预测函数放在了一起：

                                                                                             (3)

此时的标签。很容易证明。显然，这种形式和第一种logistic回归本质上没有区别。既然两种形式是等价的，为了适应更加广泛的分类Loss最小化框架，我们使用第二种形式来表示Logistic回归。

首先定义为样本标签，为特征向量。该分类Loss最小化框架可以表示为：

                                                       

这里使用的Loss函数即为Logistic Loss函数。实际上，我们可以通过该Loss最小化框架得到极大似然法则。如果将Logistic回归第二种表示形式代入到此时的，可得：

                                    

由此，Loss最小化可以表示为：

                                         

上式等式最后即为极大似然估计的表示形式。也就是说，Logistic回归模型使用的Loss函数为Logistic Loss函数，使用极大似然估计法的目的是为了使得该Loss函数最小。