【ML实验5】SVM(手写数字识别、核方法)
实验代码获取 github repo
山东大学机器学习课程资源索引
实验目的
实验内容
这里并不是通过 KTT 条件转化,而是对偶问题和原问题为强对偶关系,可以通过 KTT 条件进行化简。
令 x = α = [ α 1 , α 2 , . . . , α n ] T x=\alpha=[\alpha_1,\alpha_2,...,\alpha_n]^T x=α=[α1,α2,...,αn]T,则有
∑ i , j = 1 m α i y ( i ) y ( j ) < x ( i ) , x ( j ) > α j \sum^m_{i,j=1}\alpha_iy^{(i)}y^{(j)}
= ∑ i = 1 m ∑ j = 1 m α i y ( i ) y ( j ) < x ( i ) , x ( j ) > α j =\sum^m_{i=1}\sum^m_{j=1}\alpha_iy^{(i)}y^{(j)}
= ∑ i = 1 m α i ∑ j = 1 m y ( i ) y ( j ) < x ( i ) , x ( j ) > α j =\sum^m_{i=1}\alpha_i\sum^m_{j=1}y^{(i)}y^{(j)}
令矩阵 H H H满足 H i j = y ( i ) y ( j ) < x ( i ) , x ( j ) > H_{ij}=y^{(i)}y^{(j)}
= ∑ i = 1 m α i ∑ j = 1 m H i j α j =\sum^m_{i=1}\alpha_i\sum^m_{j=1}H_{ij}\alpha_j =∑i=1mαi∑j=1mHijαj
= ∑ i = 1 m α i H i α =\sum^m_{i=1}\alpha_iH_{i}\alpha =∑i=1mαiHiα
= α T H α = x T H x =\alpha^TH\alpha=x^THx =αTHα=xTHx
其实,基于同样的技巧, H H H 矩阵可以写成 H = Y T X X T Y = ( Y . ∗ X ) ( Y . ∗ X ) T H=Y^TXX^TY=(Y.*X)(Y.*X)^T H=YTXXTY=(Y.∗X)(Y.∗X)T.
其中, ( X X T ) i j = x ( i ) ( x ( j ) ) T = < x ( i ) , x ( j ) > (XX^T)_{ij}=x^{(i)}(x^{(j)})^T=
code 中将较小的 a l p h a alpha alpha 默认为0,因为求解器用的是迭代方法,返回数值解,可能收敛到一个很小但不为0的值;
其他 a l p h a alpha alpha 对应的是 support vector,代入公式计算 ω ∗ \omega^* ω∗ 和 b ∗ b^* b∗.
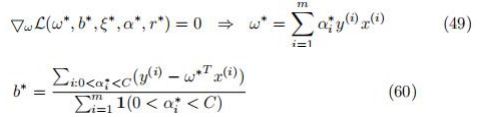
code
% 构建目标函数
H = zeros(m);
for i = 1 : m
for j = 1 : m
H(i, j) = y(i) * y (j) * x(i, :) * x(j, :)';
end
end
% H = (y .* x) * (y .* x)';
% H = (H + H') / 2;
f = (-1) * ones(m, 1);
% 构建约束
Aeq = y';
beq = 0;
lb = zeros(m, 1);
ub = zeros(m, 1);
ub(:) = C;
% 利用quadprog求解器求解对偶问题
% quadprog(H,f,A,b,Aeq,beq,lb,ub)
[alpha, fval] = quadprog(H, f, [], [], Aeq, beq, lb, ub);
% 求support vector
alpha(find(alpha < 1e-8)) = 0;
sv = find(alpha > 0 & alpha < C);
w = 0; % omega
for i = 1 : length(sv)
w = w + alpha(sv(i)) * y(sv(i)) * x (sv(i), :)';
end
num = y - x * w;
b = sum(num(sv)) / length(sv);
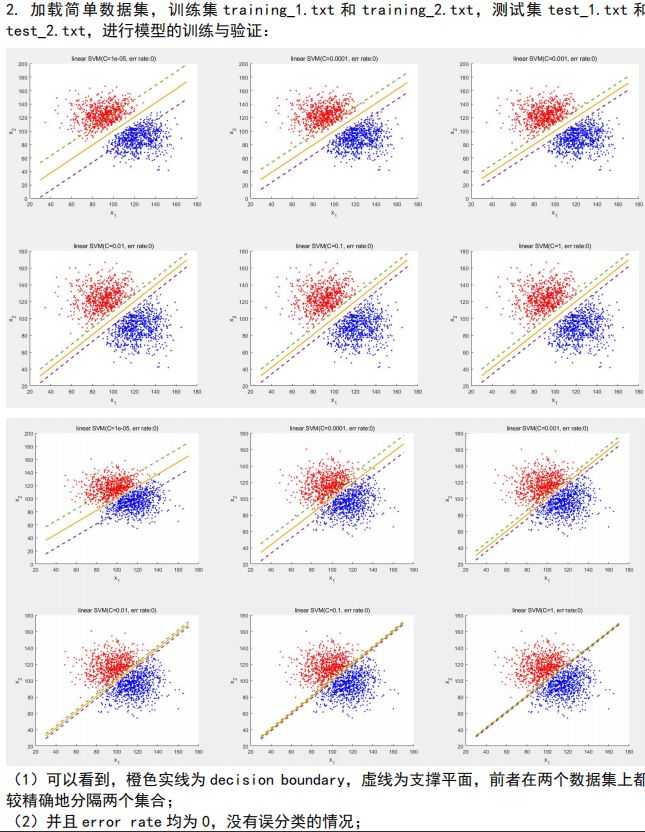
在 linear-separable 数据集上验证
正则项参数C变化,带来优化目标的“倾斜”,但是 margin 和 C 很难发掘出精确的代数关系(经过一个非线性问题的求解),只能说明它们的相关性。
做手写数字识别(仅有0和1):
由于训练集太大,采用不重复采样:
m = length(x);
% 使用全部训练集,H矩阵大小为12665*12665,运算巨大,耗时较久
% 因此采样部分训练集,大小为tr_size
rp = randperm(m);
tr_size = 1000;
samp = rp(1 : tr_size);
x = x(samp, :); y = y(samp);
m = length(x);
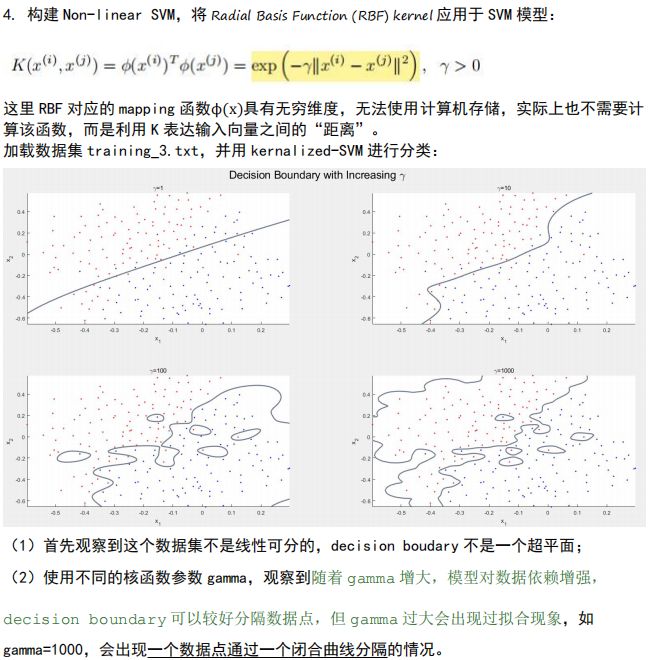
核方法
预处理 kernal matrix,之后将 < x ( i ) , x ( j ) >
% 获取基于核函数Radial Basis Function计算的关系矩阵kmat
function kmat = get_kernel_mat(x, gamma)
kmat = [];
for i = 1 : length(x)
for j = 1 : length(x)
kmat(i, j) = exp(-gamma * norm(x(i, :) - x(j, :)) ^ 2);
end
end
end
之后,决策函数不直接计算,也无法计算,因为 mapping 函数具有无穷维度,实际上通过 k m a t kmat kmat 可以绕过直接计算 mapping ,如下图,实际就是代换 ω ∗ \omega^* ω∗,可以得到 ϕ T ( x ( i ) ) ϕ ( x ( j ) ) \phi^T(x^{(i)})\phi(x^{(j)}) ϕT(x(i))ϕ(x(j)).
Mark the usage of contour func:
Here since vals only have two values 1 and -1,contour lines also become the boundaries.
% Make classification predictions over a grid of values
xplot = linspace(min(x(:, 1)), max(x(:, 1)), 100)';
yplot = linspace(min(x(:, 2)), max(x(:, 2)), 100)';
[X, Y] = meshgrid(xplot, yplot);
vals = zeros(size(X));
% For each point in this grid, you need to compute its decision
% value. Store the decision values in vals.
% ...
hold on
plot(x(pos, 1), x(pos, 2), '.r');
plot(x(neg, 1), x(neg, 2), '.b');
xlabel('x_1'); ylabel('x_2');
str = strcat('\gamma=', num2str(gamma(t)));
title(str);
% Plot the SVM boundary
colormap bone;
contour(X, Y, vals, [0 0], 'LineWidth', 2);