第一性原理(DFT)基础知识
文章目录
-
-
- 1.计算模拟介绍
-
-
- 1.科学研究范式
- 2.计算模拟的作用
- 3.计算模拟的应用范围
-
- 2.第一性原理基础(DFT)
-
-
- 1.第一性原理
- 2.密度泛函理论
- 3.薛定谔方程
- 4.绝热近似(Born-Oppenhemer)
- 5.单电子近似
- 6.Hartree-Fock-Roothaan方程
- 7.Hohenberg-Kohn定理
- 8.Kohn-Sham方程
- 9.赝势平面波
- 10.泛函分类与K点
-
-
1.计算模拟介绍
1.科学研究范式
科学研究方法(范式)发展历程:
- 科学实验:在研究方法上归纳为主,带有较多盲目性的观测和实验
- 模型归纳:偏重理论总结和理性概括,在研究方法上以演绎法为主
- 模型仿真:根据现有理论的模拟仿真计算,再进行少量的实验验证
- 数据驱动:以大量数据为前提,运用机器学习、数据挖掘技术,可以从大量已知数据中得到未知理论。
源自:图灵奖得主Jim Gray在NRC-CSTB上的报告
2.计算模拟的作用
- 预测:探究材料结构,研究材料性能
- 解释:解释实验现象,探究反应机理
3.计算模拟的应用范围
在许多物理学和工程领域,取得科学和技术进步的关键在于能够从原子或分子尺度理解并调控物质的性质。
- 量子力学(Atom < 1000,Time < ps)
- 热力学量、分子微观结构
- 分子稳定性、反应机理
- 光谱、频率强度
- 预测反应位点、反应性
- 分子间的相互作用
- 电子结构分析
- 分子动力学(Atom < 1000000,Time < ns)
- 热力学量、分子宏观构型
- 光谱、频率强度
- 分子间的相互作用
- 环境(密度、压强、体积、温度)
- 宏观性质(黏度、玻璃化温度、熔点)
- 迁移性质(扩散、RDF、MSD)
- 化学反应(裂解、合成、反应速率)
2.第一性原理基础(DFT)
1.第一性原理
英文名称:First Principle
第一性:根据原子核和电子的相互作用的原理及其基本运动规律,运用量子力学原理,从具体要求出发,经过一些近似处理后直接求解薛定谔方程的算法。
常用近似求解:半经验、第一性原理(Hartree-Fock、密度泛函理论DFT)
2.密度泛函理论
英文全称:Density functional theory (DFT)
密度:电子密度为唯一变量
泛函:能量是密度的函数,密度是坐标的函数,函数的函数为泛函。 E [ ρ ( r ) ] E[\rho (r)] E[ρ(r)]
3.薛定谔方程
定态薛定谔方程: H ^ ψ = E ψ \hat{H} \psi =E\psi H^ψ=Eψ
近似求解多粒子系统的薛定谔方程
哈密顿算符: H ^ = ∑ α = 1 p − ℏ 2 2 M α ⏟ + ∑ i = 1 N − ℏ 2 2 m e ∇ i 2 ⏟ − ∑ i = 1 N ∑ α = 1 p Z α e 2 r i α ⏟ + ∑ i = 1 N ∑ j > i e 2 r i j ⏟ + ∑ α = 1 p ∑ β > α Z α Z β e 2 R α β ⏟ \hat{H}=\underbrace{\sum_{\alpha =1}^{p}-\frac{\hbar^{2}}{2M_{\alpha}}}+\underbrace{\sum_{i=1}^{N}-\frac{\hbar^{2}}{2m_{e}}\nabla_{i}^{2}}-\underbrace{\sum_{i=1}^{N}\sum_{\alpha=1}^{p}\frac{Z_{\alpha}e^{2}}{r_{i\alpha}}}+\underbrace{\sum_{i=1}^{N}\sum_{j>i}\frac{e^{2}}{r_{ij}}} +\underbrace{\sum_{\alpha=1}^{p}\sum_{\beta>\alpha}\frac{Z_{\alpha}Z_{\beta}e^{2}}{R_{\alpha\beta}}} H^= α=1∑p−2Mαℏ2+ i=1∑N−2meℏ2∇i2− i=1∑Nα=1∑priαZαe2+ i=1∑Nj>i∑rije2+ α=1∑pβ>α∑RαβZαZβe2
其组成依次为:核动能、电子动能、核与电子的相互作用、电子与电子的相互作用、核与核的相互作用
拉普拉斯算符: ∇ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 \nabla^{2}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}} ∇2=∂x2∂2+∂y2∂2+∂z2∂2
4.绝热近似(Born-Oppenhemer)
核的质量 M α M_{\alpha} Mα远大于电子的质量 m e m_{e} me(1836倍),因此电子运动速率的变化比核快的多,核可以视为静止不动。如果构型有变化,电子可以迅速调整变成与之相应的状态。
体系波函数 ψ \psi ψ分离变量:核波函数 v ( R → ) v\left(\overrightarrow{R}\right) v(R)和电子波函数 u ( R → , r → ) u\left(\overrightarrow{R},\overrightarrow{r}\right) u(R,r)
E v = − ∑ α 1 2 M α ∇ α 2 v + E ′ ( R → ) v E ′ ( R → ) u = − ∑ i 1 2 ∇ i 2 + V ( R → , r → ) u Ev=-\sum_{\alpha}\frac{1}{2M_{\alpha}}\nabla^{2}_{\alpha}v+E'\left(\overrightarrow{R}\right)v\\E'\left(\overrightarrow{R}\right)u=-\sum_{i}\frac{1}{2}\nabla^{2}_{i}+V\left(\overrightarrow{R},\overrightarrow{r}\right)u Ev=−α∑2Mα1∇α2v+E′(R)vE′(R)u=−i∑21∇i2+V(R,r)u
计算过程:
1.给定一组核坐标,可以得到电子运动能量 E ′ ( R → ) E'\left(\overrightarrow{R}\right) E′(R)和 u ( R → , r → ) u\left(\overrightarrow{R},\overrightarrow{r}\right) u(R,r);
2.将所有可能构型下的 E ′ ( R → ) E'\left(\overrightarrow{R}\right) E′(R)都算出来,即可得到总能量及 v ( R → ) v\left(\overrightarrow{R}\right) v(R);
3.最终得到的 E ′ ( R → ) E'\left(\overrightarrow{R}\right) E′(R)即为势能面,包含不同分子构型对应的体系能量。
5.单电子近似
在绝热近似的基础上忽略了核的运动,只需要考虑电子的运动。此时多电子的原子体系的哈密顿算符就可以写为:
H ^ = ∑ i = 1 N − ℏ 2 2 m e ∇ i 2 ⏟ − ∑ i = 1 N Z e 2 r i ⏟ + ∑ i = 1 N ∑ j > i e 2 r i j ⏟ \hat{H}=\underbrace{\sum_{i=1}^{N}-\frac{\hbar^{2}}{2m_{e}}\nabla_{i}^{2}}-\underbrace{\sum_{i=1}^{N}\frac{Ze^{2}}{r_{i}}}+\underbrace{\sum_{i=1}^{N}\sum_{j>i}\frac{e^{2}}{r_{ij}}} H^= i=1∑N−2meℏ2∇i2− i=1∑NriZe2+ i=1∑Nj>i∑rije2
其组成依次为:电子动能、核-电子吸引势、电子间互斥
求解单电子的薛定谔方程:
[ − 1 2 ∇ i 2 − Z r i + V ( r i ) ] ψ i = E i ψ i \left[-\frac{1}{2}\nabla_{i}^{2}-\frac{Z}{r_{i}}+V\left(r_{i}\right)\right]\psi_{i}=E_{i}\psi_{i} [−21∇i2−riZ+V(ri)]ψi=Eiψi
1.产生初猜波函数(一般由半经验方法产生)
2.构造每个电子的哈密顿算符
3.求解所有单电子薛定谔方程,得到一组新的单电子轨道
4.新的单电子轨道作为初猜,重复2 3,直到达到收敛阈值
如何求解 i i i电子与N-1个电子的互斥?Hartree-Fock方程
判断收敛
收敛标准EDIFF
6.Hartree-Fock-Roothaan方程
对于分子来说,可以认为分子中的电子都处在各自的轨道上,其构型与原子的空间位置相关,体系的波函数可以写成各原子轨道的线性组合(LCAO-MO):
Φ = ∣ ψ 1 ( q 1 ) ψ 2 ( q 2 ) . . . ψ N ( q N ) ∣ \Phi=\left|\psi_{1}(q_{1})\psi_{2}(q_{2})...\psi_{N}(q_{N})\right | Φ=∣ψ1(q1)ψ2(q2)...ψN(qN)∣
LCAO-MO结合Hartree-Fock方程,得到了Hartree-Fock-Roothaan方程:
F C = S C ε , F 为 F o c k 矩阵, S 表示重叠积分, C 为系数矩阵 FC=SC\varepsilon,F为Fock矩阵,S表示重叠积分,C为系数矩阵 FC=SCε,F为Fock矩阵,S表示重叠积分,C为系数矩阵
其核心理念为将分子轨道朝基函数集合展开
ϕ i = ∑ μ c u , i χ u ( i = 1 , 2 , 3... N ) \phi_{i}=\sum_{\mu}c_{u,i}\chi_{u}(i=1,2,3...N) ϕi=μ∑cu,iχu(i=1,2,3...N)
自洽场迭代求解Hartree-Fock-Roothaan方程:
1.确定基函数集合 χ u \chi_{u} χu
2.由基函数确定各种积分(S)
3.假设一组初始的分子轨道(C )
4.构造Fock矩阵
5.解Hartree-Fock-Roothaan方程,得到轨道能量,新的系数矩阵C,总能量
6.判断收敛,否则重复4 5过程,是则退出迭代
7.Hohenberg-Kohn定理
由于上述计算是基于Hartree-Fock-Roothaan方程,但是HF方法并没有很好的考虑电子之间的排斥。比如,交换相关(自旋相同的电子之间存在排斥,泡利不相容原理)、库伦相关(电子之间存在库伦排斥)。
通常通过后HF方法和密度泛函理论来校正相关能。后HF方法,包括组态相互作用、微扰、耦合簇、多组态自洽场和多参考方法。
1964年,Hohenberg和Kohn提出如下定理:1.HK第一定理:体系基态下的电子密度分布决定了体系基态的哈密顿以及一切性质;2.HK第二定理:对于任意体系的电子密度分布,在精确能量泛函下,其对应的能量一定高于真实基态密度对应的真实基态能量。
8.Kohn-Sham方程

1965年,Kohn及Sham给出了由电子密度构造能量的方法。
Kohn-Sham方程求解
1.各原子的电子密度叠加作为分子电子密度初始值 ρ ( r → ) \rho(\overrightarrow{r}) ρ(r)
2.根据 ρ ( r → ) \rho(\overrightarrow{r}) ρ(r)求得交换相关能,代入KS方程得到初始KS轨道
3.确定基函数集合 χ u \chi_{u} χu
4.由基函数确定各种积分(S)
5.假设一组初始的分子轨道(C )
6.构造Fock矩阵
7.解Kohn-Sham方程,得到轨道能量,新的系数矩阵C,总能量
8.判断收敛,否则重复6 7过程,是则退出迭代
9.赝势平面波
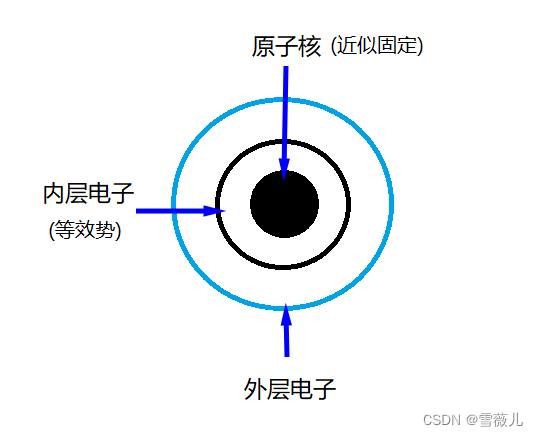
内层电子的主要作用:屏蔽原子核的势。
赝势:“冷冻”内层电子,将其主要作用等效为一个有效势。
平面波:一种基函数,适用于固体和表面这种在空间中无限延展的体系。
赝势选择:每种元素往往有多种赝势存在,可分为硬赝势(其中ENMAX较大)、软赝势(其中ENMAX较小)。
平面波动能截ENCUT(≥ENMAX):以平面波展开波函数,每个本征值对应的波函数都是选用的平面波的线性叠加。
10.泛函分类与K点
泛函分类:
1.LDA ☆☆:低估基态能量、键长、晶格常数、电离能,高估结合能。不适合小分子、金属体系计算,大体系下可得到较为精确的能量。
2.GGA ☆☆☆:没考虑范德华相互作用,低估结合能、电子亲和能和电离能,高估键长、晶格常数。更精确的能量,更可靠的相互作用。(计算吸附能,需要额外考虑范德华相互作用)。
3.meta-GGA ☆:性质计算相比GGA改进不大,部分泛函带隙计算精度更高。
4.hybrid GGA hybrid meta-GGA ☆☆☆:收敛成功率相对GGA较低,性质计算比GGA更准确。
5.double hybrids ☆:计算成本剧增,适合极小体系计算。性质计算更为准确。
不同理论去精确求解交换相关能精度和耗时不同,尽量选择高精度、成本小的泛函:纯泛函(LDA,GGA(PBE、PEBsol、AM05)),杂化泛函(HSE06、PBE0、B3LYP)。
什么是K点?
k-vector是倒空间(动量空间)的基本构成点,只取在一个倒空间晶格向量的范围内来描述k。
K点在模拟中的作用?
总能量计算是对布里渊区内的波函数进行积分,积分是通过对部分特殊K点的求和完成的。**K点越密,能量越准确。**合适的K点可以在保证计算精度的同时降低计算成本。