02-机器学习中的模型评估

01. 前言

本章节将介绍机器学习中常见的评价指标。其实在面对不同的问题是，不同的算法有不同的性能评估，比如分类问题与回归问题，它们的评价指标就不能用同一个。本章节用通俗点的语言来说明一些常用的评价指标，如有不正确的地方或描述不太恰当的地方，随时欢迎批评！

02. 正文

【1】 下面介绍几个分类任务的评价指标

1. 精度与错误率
假设有 m 个样本，每一个样本经过训练后都会得到一个预测值，预测值的意思是经过训练后，每个样本会被输入到一个负责预测的代码当中，然后会得到一个预测值，可以认为1表示分类正确，0表示分类错误。那么假设有 n 个预测错误的样本，则： $$错误率=\frac{n}{m}$$ $$精度=1-错误率=1-\frac{n}{m}$$

• 提一点，这两个指标在分类任务用的比较多。
  
  

2. 混淆矩阵
混淆矩阵如下：

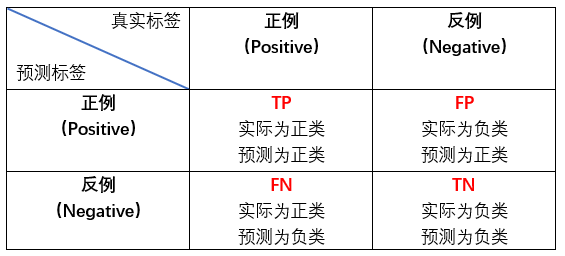
• T/F：表示预测结果，P/N：表示样本结果。首先要搞清楚这两个的不同区别。比如 FP表示的是样本实际值为负类，但是模型却将它归类为正类。

看到这可能有人会问了，为什么会有 “实际为负类” 的东西？我们以猫分类问题为例子，假设猫的样本为Positive，那么除了猫以外的样本均为Negative，假设还有牛羊之类（为负类）的吧！那么假设我把一堆样本都放进去训练，就会出现上面四个情况，到这应该懂了吧？
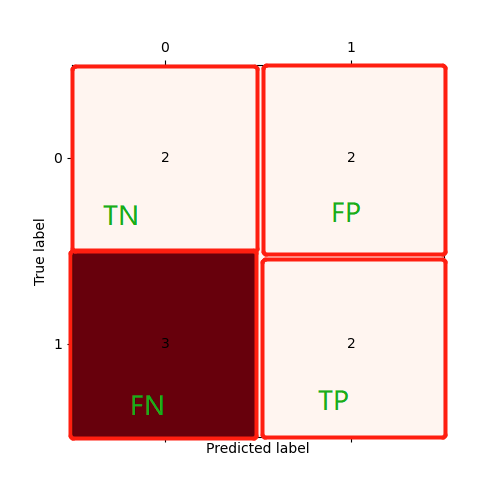
案例展示：

from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt

# 假设这里有九个样本，其中0代表Negative，1代表Positive
y_true = ["0", "0", "0", "0", "1", "1", "1", "1", "1"]
# 这里有九个预测值，0代表False，1代表True
y_pred = ["0", "0", "1", "1", "0", "0", "1", "1", "0"]
# 可以看到: 这里TP=2(7.8), TN=2(1.2), FP=2(3.4), FN=3(5.6.9)
C = confusion_matrix(y_true, y_pred)
plt.matshow(C, cmap=plt.cm.Reds) # 根据最下面的图按自己需求更改颜色
for i in range(len(C)):
    for j in range(len(C)):
        plt.annotate(C[j, i], xy=(i, j), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()

结果如下：

3. 准确率、精准率和召回率
这三个指标是由混淆矩阵衍生出来的，它们具体公式如下：
$$\begin{gathered} 精准度accuracy=\frac{TP+TN}{TP+TN+FP+FN} \\ 准确率Precision=\frac{TP}{TP+FP} \\ 召回率Recall=\frac{TP}{TP+FN} \end{gathered}$$

• 精准度accuracy：个人认为有点像上面讲的精度，就是分类正确的样本除以总样本数。
• 准确率Precision：分类器预测的正样本中预测正确的比例，取值越大，模型预测能力越好。
• 召回率Recall：类器所预测正确的正样本占所有正样本的比例，取值越大，模型预测能力越好。

看完上面的解释，感觉如同废话？其实 Precision 和 Recall 都在关注TP，但是角度不一样，Precision 看的是在所有正样本的目标下，实际的精准度有多少，而 Recall 则看的是所有的“真的”中有多少“我认为真的”。当遇到分类问题时，具体看你更关注哪个指标就使用哪个指标，并根据数学方法调整大小。

4. F1 score
其公式如下：
$$F1score=\frac{2\times Precision\times Recall}{Precision+Recall}$$
F1 score同时关注了 Precision 和 Recall ，相对来说会更加客观一点，个人也是比较推荐这一指标多一点！当然这仅代表个人观点。关于F1 score的内容，在西瓜书上也有更多拓展知识讲解，我这里讲的是较为常用的一个。

5. P-R曲线
这里借用西瓜书的一张图：
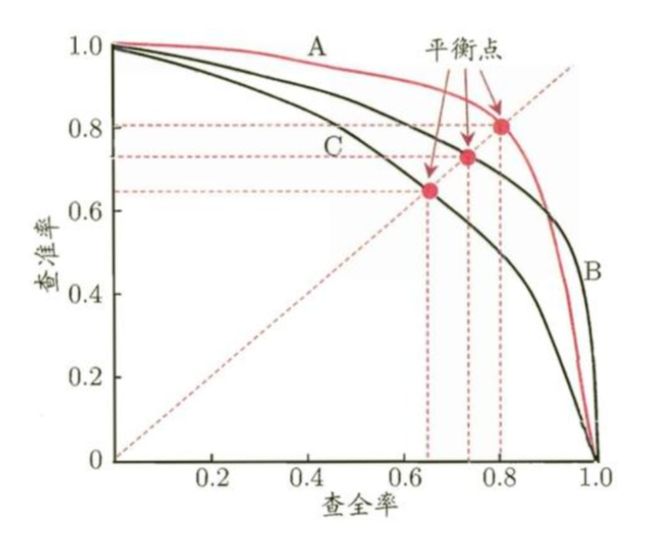查准率就是准确率 Precision，查全率就是召回率 Recall。P-R曲线就是把准确率和召回率以图形的方式描绘出来了，这样更为直观，便于工程师调试。

6. ROC和AUC
关于这部分内容，如果要详细说的话篇幅太长了，如果有兴趣了解的话，可以去这个链接看：https://mp.weixin.qq.com/s/3WwhMWtTL97SwGlK4h6FvQ，讲的也十分详细！最主要的还是学会前面提到的几个指标，用的比较多，等学有所成了，再深究更多内容！
把上面的例子用代码演示一下：

import numpy as np
from sklearn.metrics import recall_score, precision_score, f1_score
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve

# 假设这里有九个样本，其中0代表Negative，1代表Positive
y_true = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1])
# 这里有九个预测值，0代表False，1代表True
y_pred = np.array([0, 0, 1, 1, 0, 0, 1, 1, 0])
# 可以看到: 这里TP=2(7.8), TN=2(1.2), FP=2(3.4), FN=3(5.6.9)

# precision = TP / (TP+FP)
Precision = precision_score(y_true, y_pred, pos_label=1)
print(Precision)    # 输出: 0.5. 因为这里设置了pos_label=1,即1设置为正类, 可以尝试设置为0, 结果为0.4, 尝试自己算一下

# recall = TP / (TP+FN)
Recall = recall_score(y_true, y_pred, pos_label=1)
print(Recall)   # 输出: 0.4

# f1 score = 2×P×R / (P+R)
F1_score = f1_score(y_true, y_pred, pos_label=1)
print(F1_score) # 输出: 0.4444444444444445

def plot(precision,recall):#画出函数图像
    fig = plt.figure(figsize=(10, 10))
    plt.xlabel('Recall')
    plt.ylabel('Precision')
    x = np.arange(0,1.0,0.2)
    y = np.arange(0,1.0,0.2)
    plt.xticks(x)
    plt.yticks(y)
    plt.plot(recall,precision)
    plt.show()

precision, recall, thresholds = precision_recall_curve(y_true, y_pred, pos_label=1)
plot(precision, recall)

【2】下面介绍几个回归任务的评价指标

首先要明白一点，回归任务得到的是一个数值，而分类任务得到的是概率值，因此回归任务得到的是一个 ≥ 0 的值。
1. 平均绝对误差（Mean Absolute Error，MAE）
平均绝对误差又叫L1范数损失，其公式如下：
$$MAE(y,\hat{y})=\frac{1}{m}\sum _{i=1}^m|y_i-\widehat{y_i}|$$
什么意思呢？y_i 就是预测值，yhat_i 就是真实值。 如果还不理解，就想象成在一个二维坐标系中存在不同位置的坐标点，这些点就是真实值，经过训练后，会得到每个样本的预测值（x相同，y可能相同），那么公式右边部分就是相当于|预测值 - 真实值|，然后在把所有值相加 ÷ 总样本数就可以了。下面举个具体例子就明白了：

假设存在4个样本，那么m=4，它们真实值=[2,4,6,8]，预测值=[4,6,8,12]
那么 MAE = （2+2+2+4）/4 = 2.5

其代码实现如下：

import numpy as np
from sklearn.metrics import mean_absolute_error

y_true = np.array([2, 4, 6, 8])
y_pred = np.array([4, 6, 8, 12])
MAE = mean_absolute_error(y_true, y_pred)
print(MAE)

2. 均方误差（Mean Squared Error，MSE）
均方误差又叫L2范数损失，其公式如下：
$$MSE(y,\hat{y})=\frac{1}{m}\sum _{i=1}^m（y_i-\widehat{y_i}{）}^2$$
该公式与 MAE 很像，只是一个求的是绝对值，一个是求平方 。同样举上面那个例子：

假设存在4个样本，那么m=4，它们真实值=[2,4,6,8]，预测值= [4,6,8,12]，
那么 MSE = （4+4+4+16）/4 = 7

其代码实现如下：

import numpy as np
from sklearn.metrics import mean_squared_error

y_true = np.array([2, 4, 6, 8])
y_pred = np.array([4, 6, 8, 12])
MSE = mean_squared_error(y_true, y_pred)
print(MSE)

3. 均方根误差（Root Mean Squared Error，RMSE）
均方根误差j计算的是预测值与真实值之间的偏差，而不是预测值与平均值之间的偏差。其公式如下：
$$RMSE(y,\hat{y})=\sqrt{\frac{1}{m}\sum _{i=1}^m（y_i-\widehat{y_i}{）}^2}$$
RMSE与MSE很像，就是加了一个根号。同样举上面的那个例子：

假设存在4个样本，那么m=4，它们真实值=[2,4,6,8]，预测值= [4,6,8,12]，
那么 RMSE = √（（4+4+4+16）/4 ）=2.65

其代码实现如下：

import numpy as np
from sklearn.metrics import mean_squared_error

y_true = np.array([2, 4, 6, 8])
y_pred = np.array([4, 6, 8, 12])
RMSE = np.sqrt(mean_squared_error(y_true, y_pred))
print(RMSE)

4. 决定系数（R squared coefficient of determination，R²）
R² 反映的是模型拟合数据的准确程度，一般R² 的范围是0到1。

• 如果结果越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好。
• 结果是0，说明模型预测不能预测因变量。
• 如果结果是1，就说明是函数关系。

其公式如下：
$$R^2(y,\hat{y})=1-\frac{SSE}{SST}=1-\frac{{\sum }_{i=1}^m(y_i-\hat{y}{)}^2}{{\sum }_{i=1}^m(y_i-\bar{y}{)}^2}=1-\frac{\frac{{\sum }_{i=1}^m(y_i-\hat{y}{)}^2}{m}}{\frac{{\sum }_{i=1}^m(y_i-\bar{y}{)}^2}{m}}$$
同样举上面那个例子：

假设存在4个样本，那么m=4，它们真实值=[2,4,6,8]，预测值= [4,6,8,12]，其中 y_true 的平均值 = 5
那么R² = 1 - （4+4+4+16）/（1+1+9+49）= 0.533

其代码如下：

import numpy as np

y_true = np.array([2, 4, 6, 8])
y_pred = np.array([4, 6, 8, 12])

r2 = 1 - (sum((y_pred - y_true)**2) / sum((y_pred - np.mean(y_true))**2))
print(r2)

03. 其他

文中的代码难度都属于入门级别的，所涉及的数据集都是一维并且不是真实的，目的是先让大家能了解并大致理解所涉及到的指标具体过程，后续会结合机器学习算法来进行真实数据实战。当然，文中内容只是冰山一角，我只是把个人认为比较常见的拿出来总结了而已。

04. 末言

最后，如果文章对你有帮助的话，可以点赞一下！ 另外，如果文章某些地方如果有错误或不严谨的地方，欢迎在评论区指正！希望大家共同进步！