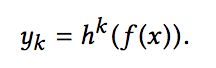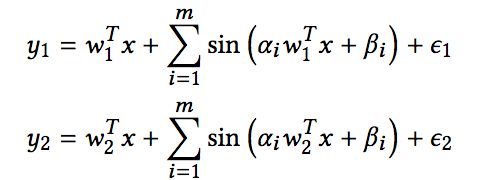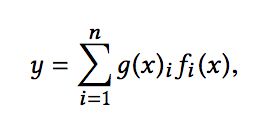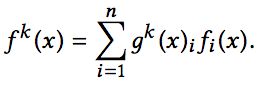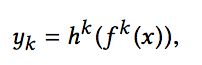RS Meet DL(68)-建模多任务学习中任务相关性的模型MMoE

本文介绍的论文题目是：《Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts》

多任务学习最近越来越受欢迎，咱们前面也介绍过几篇阿里多任务学习的模型，不过多任务学习的效果受不同任务之间的相关性影响较大，因此本文基于Mixture-of-Experts (MoE)模型，提出了一种显式建模任务相关性的模型Multi-gate Mixture-of-Experts (MMoE) ，一起来学习一下。

1、背景

近年来，深度神经网络的应用越来越广，如推荐系统。推荐系统通常需要同时优化多个目标，如电影推荐中不仅需要预测用户是否会购买，还需要预测用户对于电影的评分，在比如电商领域同时需要预测物品的点击率CTR和转化率CVR。因此，多任务学习模型成为研究领域的一大热点。

许多多任务学习模型取得了不错的效果，但是实践中多任务学习模型并不总比单任务模型效果更突出。这主要是因为不同任务之间的相关性低（如数据的分布不同等等）导致的。

是不是真的如上述所说，任务之间的相关性会影响多任务学习的效果呢，咱们先在第二节中做一个实验。

2、任务相关性实验

2.1 一般的多任务学习模型框架

一般的多任务学习模型框架如下：

对于不同的任务，底层的参数和网络结构是共享的，然后上层经过不同的神经网络得到对应任务的输出。假设底层输出是f(x)，那么第k个任务的输出yk为：

其中hk是第k个任务上层神经网络的参数。

2.2 任务相关性实验

接下来，我们通过一个实验来探讨任务相关性和多任务学习效果的关系。

假设模型中包含两个回归任务，而数据通过采样生成，并且规定输入相同，输出label不同。那么任务的相关性就使用label之间的皮尔逊相关系数来表示，相关系数越大，表示任务之间越相关，数据生成的过程如下：

首先，生成了两个垂直的单位向量u1和u2，并根据两个单位向量生成了模型的系数w1和w2，如上图中的第二步。w1和w2之间的cosine距离即为p，大伙可以根据cosine的计算公式得到。

随后基于正态分布的到输入数据x，而y根据下面的两个式子的到：

注意，这里x和y之间并非线性的关系，因为模型的第二步是多个sin函数，因此label之间的皮尔逊相关系数和参数w1和w2之间的cosine距离并不相等，但是呈现出一个正相关的关系，如下图：

因此，本文中使用参数的cosine距离来近似表示任务之间的相关性。

2.3 实验结果

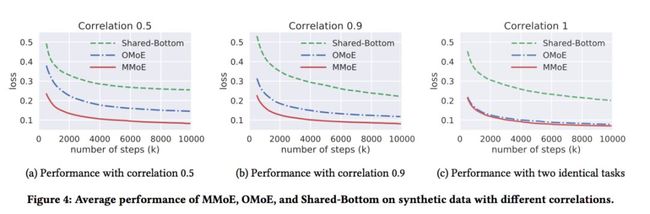
基于上述数据生成过程以及任务相关性的表示方法，分别测试任务相关性在0.5、0.9和1时的多任务学习模型的效果，如下图：

可以看到的是，随着任务相关性的提升，模型的loss越小，效果越好，从而印证了前面的猜想。

3、MMoE模型

3.1 MoE模型

先来看一下Mixture-of-Experts (MoE)模型（文中后面称作 One-gate Mixture-of-Experts (OMoE)），如下图所示：

可以看到，相较于一般的多任务学习框架，共享的底层分为了多个expert，同时设置了一个Gate，使不同的数据可以多样化的使用共享层。此时共享层的输出可以表示为：

其中fi代表第i个expert的输出，gi代表第第i个expert对应的权重，是基于输入数据得到的，计算公式为g(x) = softmax(Wgx)。

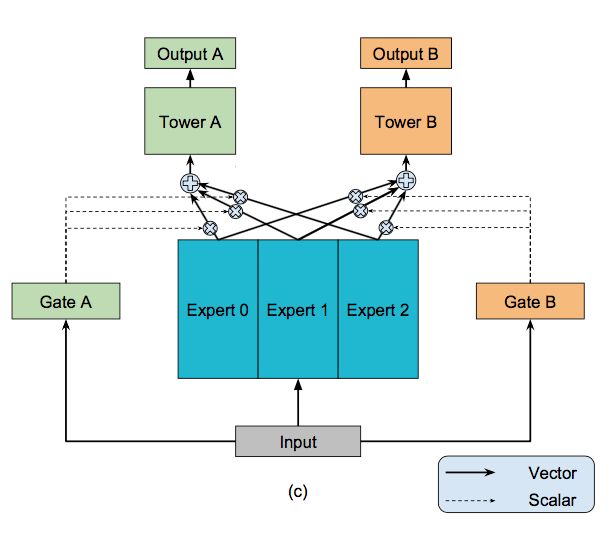
3.2 MMoE模型

相较于MoE模型，Multi-gate Mixture-of-Experts (MMoE)模型为每一个task设置了一个gate，使不同的任务和不同的数据可以多样化的使用共享层，模型结构如下：

此时每个任务的共享层的输出不同，第k个任务的共享层输出计算公式如下：

随后每个任务对应的共享层输出，经过多层全连接神经网络得到每个任务的输出：

从直观上考虑，如果两个任务并不十分相关，那么经过Gate之后，二者得到的权重系数会差别比较大，从而可以利用部分expert网络输出的信息，近似于多个单任务学习模型。如果两个任务紧密相关，那么经过Gate得到的权重分布应该相差不多，类似于一般的多任务学习框架。

4、实验结果

先回顾上面介绍的三种多任务学习的架构：

实验分为三部分：人工合成数据集（即本文第二部分所介绍的人工生成的数据集）、UCI census-income dataset和Large-scale Content Recommendation

4.1 人工合成数据集-实验结果

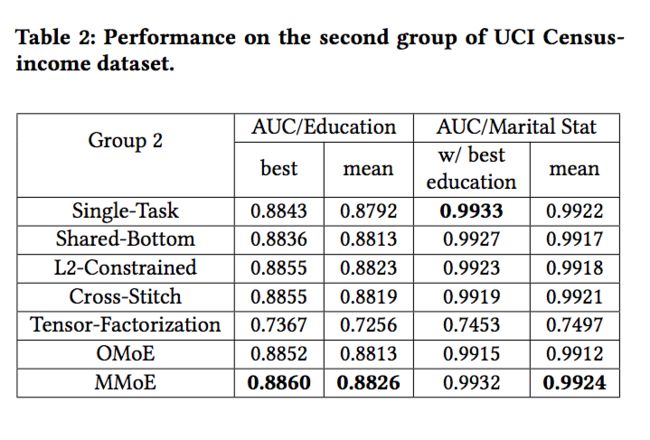
4.2 UCI census-income dataset-实验结果

这块文中介绍了几种多任务学习的模式，这里就不过多介绍了。

4.3 Large-scale Content Recommendation-实验结果

这篇论文的介绍就到这里啦，这一篇是在我阅读youtube多任务学习论文中发现的，所以下一篇会介绍youtube今年的论文《Recommending What Video to Watch Next: A Multitask Ranking System》，期待一下吧。

可能我的理解还有不到位的地方，欢迎大家一起讨论对这篇文章的理解~