自然语言处理学习笔记-lecture2-数学基础1-微积分

微积分

函数

设数集$D\subset \mathbb{R}$，则称映射$f:D\subset \mathbb{R}$为定义在$D$上的函数，通常记为 $y=f(x),x\in D$，其中$x$称为自变量，$y$称为因变量，$D$称为定义域，记作$D_f$，即$D_f=D$。
对于每个$x\in D$，按对应法则$f$，总有唯一的值$y$与之相对应，这个值称为函数$f$在$x$处的函数值，记作$f(x)$，即$y=f(x)$。函数值$f(x)$的全体所构成的集合称为函数f的值域，记作$R_f$或$f(D)$，即
$$R_f=f(D)=\{y|y=f(x),x\in D\}$$
例如，$f(x)=3x+2$是一个函数，定义域是$R$，值域是$R$，自变量和因变量之间存在一一映射。表示函数的记号可以任意选取，除了常用的$f$以 外，还可以用其他的英文字母或希腊字母，如$g$、$F$和$\varphi$。

复合函数

给定两个函数$f$和$g$，复合函数定义为:
$$(f\circ g)(x)=f(g(x))$$
两个函数$f$和$g$能构成复合函数$f\circ g$的条件是:函数$g$的值域$R_g$必须是函数$f$ 的定义域$D_f$的子集，即$R_g\subseteq D_f$。
例如，$y=f(u)=3u+2$的定义域为$\mathbb{R}$，而$u=g(x)=x2-2$的定义域为$\mathbb{R}$。由于$g(R)\subseteq R$，因此$f$和$g$可以构成复合函数

导数

设函数$y=f(x)$在点$x_0$的某个邻域内有定义，当自变量$x$在$x_0$处有增量$\Delta x$， 而且$x_0+\Delta x$也在该邻域内时，函数取得增量$\Delta y=f(x_0+\Delta x)-f(x_0)$。如 果$\Delta y$与$\Delta x$之比当$\Delta x\to 0$时极限存在，则称函数$y=f(x)$在点$x_0$处可导， 并称这个极限为函数$y=f(x)$在点$x_0$处的导数，记作:
$$f^{\prime }(x_0)=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

导函数

如果函数$y=f(x)$在开区间内每一点都可导，则称函数$f(x)$在区间内可导。这时函数$y=f(x)$对于区间内的每一个确定的$x$值，都对应着一个确定的导数值，这就构成一个新的函数。我们将该函数称之为原来函数的导函数，记作$y\prime$、$f\prime (x)$或$df(x)/dx$，简称导数。

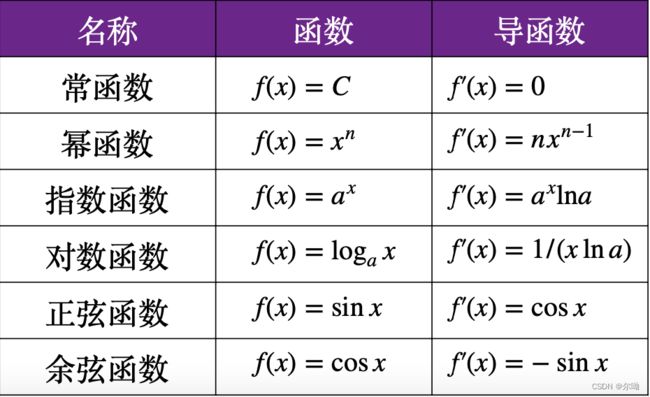
导数的四则运算

对于可导函数$f$和$g$，导数的四则运算规则如下:

• 加法: $(f+g{)}^{\prime }=f^{\prime }+g^{\prime }$
• 减法: $(f-g{)}^{\prime }=f^{\prime }-g^{\prime }$
• 乘法: $(fg)\prime =f^{\prime }g+f{g}^{\prime }$
• 除法: $(f/g{)}^{\prime }=(f^{\prime }g-f{g}^{\prime })/g^2$

复合函数的导数

对于复合函数$(f\circ g)(x)$，通常使用链式法则计算其导数:
$$(f\circ g{)}^{\prime }(x)=f^{\prime }(g(x))g^{\prime }(x)$$
令$u=g(x)$，则链式法则的另一种表述方式为:
$$\frac{df(g(x))}{dx}=\frac{df(u)}{du}\times \frac{du}{dx}$$

二阶导数

一般而言，函数$y=f(x)$的导数$y\prime =f\prime (x)$仍然是$x$的函数，可以进一步求 导。二阶导数是原函数导数的导数，即对原函数进行二次求导，记作:
$$y^{\prime \prime }=(y^{\prime }{)}^{\prime }$$
二阶导数的另一种常见的表示方法为
$$y^{\prime \prime }=\frac{d^{2}y}{d{x}^2}$$
例如，$y=x^2$的一阶导数为$y^{\prime }=2x$，而二阶导数则是一阶导数$y^{\prime }=2x$的导数y′′ = 2。
二阶导数反映了一阶导数的变化率。我们通常使用二阶导数来判断函数的凹凸性并计算极值。类似地，在条件允许的情况下，还可以计算函数的三阶导数、四阶导数或高阶导数。

函数的单调性

设函数$f(x)$的定义域为$D$，区间$I\subset D$。如果对于区间$I$上任意两点$x_1$和$x_2$， 当$x_1<x_2$时，恒有$f(x_1)<f(x_2)$，则称函数$f(x)$在区间$I$上单调递增。
反之，如果对于区间$I$ 上任意两点$x_1$ 和$x_2$ ，当$x_1<x_2$ 时，恒有 $f(x_1)>f(x_2)$，则称函数$f(x)$在区间$I$上单调递减。

凹函数

给定函数$f:\mathbb{R}\to \mathbb{R}$，对于任意两个点$x_1$和$x_2$，如果满足下列条件：
$$f\left(\frac{x_1+x_2}{2}\right)\le \frac{f(x_1)+f(x_2)}{2}$$

凸函数

给定函数$f:\mathbb{R}\to \mathbb{R}$，对于任意两个点$x_1$和$x_2$，如果满足下列条件：
$$f\left(\frac{x_1+x_2}{2}\right)\ge \frac{f(x_1)+f(x_2)}{2}$$

函数的极值

设函数$f(x)$在点$x=x_0$及其附近有定义。如果对于$x_0$附近的所有点都有 $f(x)<f(x_0)$，则$f(x_0)$是函数$f(x)$的一个极大值，$x_0$是函数$f(x)$的一个极大值点。如果对于$x_0$附近的所有点都有$f(x)>f(x_0)$，则$f(x_0)$是函数$f(x)$的一个 极小值，$x_0$是函数$f(x)$的一个极小值点。

函数的最值

函数在整个定义域内可能有许多极大值或极小值，而且某个极大值不一 定大于某个极小值。函数f(x)在整个定义域内的最小函数值$f(x_0)$称为函数 $f(x)$的最小值，$x_0$称为最小值点。类似地，函数$f(x)$在整个定义域内的最大函数值$f(x_0)$称为函数$f(x)$的最大值，$x_0$称为最大值点。
如果函数$f(x)$在闭区间$[a,b]$上连续，则$f(x)$在$[a,b]$上必有最大值和最小值。在开区间$(a,b)$上连续的函数$f(x)$不一定有最大值和最小值，如函数$f(x)=1/x$。函数的最值点必在函数的极值点或者区间的端点处获得。函数的极值可能有多个，但是最值最多只有一个。
如果函数$f(x)$在闭区间$[a,b]$上有定义，在开区间$(a,b)$内有导数，则求函数f(x)在闭区间$[a,b]$上的最大值和最小值的步骤如下:

• 求函数$f(x)$在开区间$(a,b)$的导数$f^{\prime }(x)$;
• 求方程$f^{\prime }(x)=0$在$(a,b)$内的解;
• 求在$(a,b)$内使$f^{\prime }(x)=0$的所有点的函数值和$f(x)$在闭区间端点处的函数值$f(a)$和$f(b)$;
• 比较上面所求的所有值，其中最大值为函数$f(x)$在闭区间$[a,b]$上的最大值，最小值为函数$f(x)$在闭区间$[a,b]$上的最小值。

例如，可以使用上述方法计算函数$f(x)=x^2-2x+1$在区间$[-2,2]$上的最大值和最小值，得到函数的最小值点是1，最大值点是−2。

不定积分

函数$f(x)$的不定积分是一个导数等于$f(x)$的函数$F$，即$F^{\prime }(x)=f(x)$。相应地，函数$F(x)$称为$f(x)$的原函数。一个函数通常有多个原函数。例如，函数$f(x)=2x$的原函数可以是$F(x)=x^2+1$，也可以是$F(x)=x^2+2$。因此，我们通常将原函数写成以下的形式:
$$\int f(x)dx=F(x)+C$$
其中，$C$表示任意常数。常见的积分公式如下:

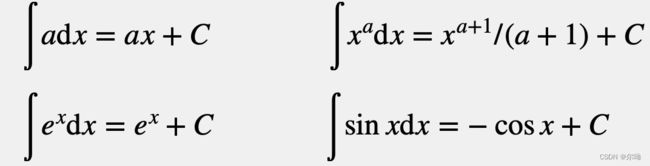
定积分

设函数$f(x)$在区间$[a,b]$上连续，将区间$[a,b]$分成$n$个长度相等的子区间，则 函数$f(x)$在区间$[a,b]$上的定积分定义为:
$${\int }_a^{b}f(x)dx=\underset{n\to +\infty }{\lim }f(a+\frac{i}{n}(b-a))\frac{b-a}{n}$$
其中，$a$称为积分下限，$b$称为积分上限，$[a,b]$称为积分区间，$x$称为积分变 量，$f(x)$称为被积函数。从直观上理解，定积分计算的是包围区域的面积。

多元函数

设$D$是一个非空的$n$元有序数组的集合，$f$为某一确定的对应法则，如果对于每一个有限数组$(x_1,x_2,...,x_n)\in D$， 通过对应法则$f$，都有唯一确定的实数$y$与之对应，则称对应法则$f$为定义在$D$上的多元函数，记为:
$$y=f(x_1,x_2,\cdots ,x_n)$$
其中$x_1,x_2,...,x_n$称为自变量，$y$称为因变量。

偏导数

设函数$z=f(x,y)$在点$(x_0,y_0)$的某一邻域内有定义，当$y$固定在$y_0$而$x$在$x_0$处 有增量$\Delta x$时，相应地函数值有增量$f(x_0+\Delta x,y_0)-f(x_0,y_0)$。如果极限
$$\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}$$
存在，则称此极限为函数$z=f(x,y)$在点$(x_0,y_0)$处对$x$的偏导数，记为:
$$\frac{\partial z}{\partial x}{|}_{x=x_0,y=y_0}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}$$
另一种形式是$f_x(x_0,y_0)$。同理可以定义函数在点$(x_0,y_0)$处对y的偏导数。如果函数$z=f(x,y)$在区域$D$内任意一点$(x,y)$处对$x$的偏导数都存在，那么这个偏导数是$x$和$y$的函数，成为函数$z=f(x,y)$对自变量$x$的偏导数，记为 $\partial z/\partial x$。

多元函数求导

设$f(x,y)=x^2+3xy+y-1$，求该函数对$x$和$y$的偏导在点$(4,-5)$处的取值。求解方法如下。首先计算函数对$x$的偏导。在计算过程中，我们可以将$y$看作常量，然后对$x$求导:
$$\frac{\partial f}{\partial x}=\frac{\partial }{\partial x}(x^2+3xy+y-1)=2x+3y$$
因此，$\partial f/\partial x$在$(4,-5)$处的值为$2\times 4+3\times (-5)=-7$。
接下来计算函数对$y$的偏导，将$x$看作常量:
$$\frac{\partial f}{\partial y}=\frac{\partial }{\partial y}(x^2+3xy+y-1)=3x+1$$
因此，$\partial f/\partial y$在$(4,-5)$处的值为$3\times 4+1=13$

多元复合函数求导

首先来考虑一元函数与多元函数复合的情况。若函数$u=\varphi (x)$和函数 $v=\psi (x)$都在点$x$可导，函数$z=f(u,v)$在对应点$(u,v)$具有连续偏导数，那 么复合函数$z=f(\varphi (x),\psi (x))$在点$x$可导，其导数为:
$$\frac{dz}{dx}=\frac{\partial z}{\partial u}\frac{du}{dx}+\frac{\partial z}{\partial v}\frac{dv}{dx}$$
例如，令$z=f(u,v)=u^2-v^2$，$u=\varphi (x)=x^2-1$，$v=\psi (x)=3x+2$，则 复合函数$z$对$x$的导数可计算为:
$$\begin{array}{rl}\frac{dz}{dx}& =\frac{\partial z}{\partial u}\frac{du}{dx}+\frac{\partial z}{\partial v}\frac{dv}{dx}\\ & =2u\times 2x+(-2v)\times 3\\ & =4x^3-10x-12\end{array}$$
然后考虑多元函数与多元函数复合的情况。如果函数$u=\varphi (x,y)$与函数 $v=\psi (x,y)$具有对$x$和$y$的偏导数，函数$z=f(u,v)$在对应点$(u,v)$具有连续偏导数，那么复合函数$z=f(\varphi (x,y),\psi (x,y))$在点$(x,y)$的两个偏导数存在:
$$\begin{gathered} \frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x} \\ \frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y} \end{gathered}$$
例如，令$z=f(u,v)=u+v$，$u=\varphi (x,y)=xy，v=\psi (x,y)=x+y$，则复合函数$z$对$x$和$y$的偏导数分别是:
$$\begin{gathered} \frac{\partial z}{\partial x}=y+1 \\ \frac{\partial z}{\partial y}=x+1 \end{gathered}$$

梯度

设二元函数$z=f(x,y)$在平面区域$D$上具有一阶连续偏导数，则对于每一 个点$(x,y)$可以定义一个向量，称为函数$z=f(x,y)$在点$(x,y)$的梯度，记作:
$$\nabla f(x,y)=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)$$
例如，令$z=f(x,y)=x^2-y^3$，则$x$和$y$的偏导函数为:
$$\frac{\partial f}{\partial x}=2x,\frac{\partial f}{\partial y}=3y^2$$
因此，函数$f(x,y)$在点$(2,1)$处的梯度是一个二维向量$(4,3)$。多元函数的梯度可以类似地计算。梯队对于计算多元函数的极值而言非常重要，在深度学习的参数优化中被广泛使用。

多元函数极值

设函数$z=f(x,y)$在点$(x_0,y_0)$的某个邻域内有定义，对于该邻域内异于 $(x_0,y_0)$的点，如果不等式
$$f(x,y)<f(x_0,y_0)$$
成立，则称函数$f(x,y)$在点$(x_0,y_0)$处有极大值。如果不等式
$$f(x,y)>f(x_0,y_0)$$
成立，则称函数$f(x,y)$在点$(x_0,y_0)$处有极小值。
例如，函数$z=3x^2+4y^2$在点$(0,0)$处有极小值，因为除了$(0,0)$以外所有的点的函数值均为正，只有在点$(0,0)$处的函数值为0。与之相反，函数$z=-\sqrt{x^2+y^2}$在点$(0,0)$处有极大值，因为除了$(0,0)$以外所有的点的函数值均为负，只有在点$(0,0)$处的函数值为0。

多元函数极值条件

定理1(必要条件):设函数$z=f(x,y)$在点$(x_0,y_0)$处具有偏导数，且在点 $(x_0,y_0)$处有极值，则函数在该点的偏导数必然为0:
$$f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$$
定理2(充分条件):设函数$z=f(x,y)$在点$(x_0,y_0)$的某邻域内连续且有一阶及二阶连续偏导数，并且$f_x(x_0,y_0)=0，f_y(x_0,y_0)=0$，令
$$f_{xx}(x_0,y_0)=A,f_{xy}(x_0,y_0)=B,f_{yy}(x_0,y_0)=C$$
则$f(x,y)$在$(x_0,y_0)$处是否取得极值的条件如下:

• 当$AC-B^2>0$时有极值，当$A<0$时有极大值，$A>0$时有极小值。
• 当$AC-B^2<0$时没有极值。
• 当$AC-B^2=0$时可能有极值，也可能没有极值。

求多元函数极值

求二元函数$f(x,y)=x^3-y^3+3x^2+3y^2-9x$的极值。
首先求解一阶导数组成的方程组:
$$\begin{gathered} f_x(x,y)=3x^2+6x-9=0 \\ {f}_y(x,y)=-3y^2+6y=0 \end{gathered}$$
得到四组解:$(1,0)、(1,2)、(-3,0)$和$(-3,2)$。它们不一定都是极值点，需要进一步考察二阶导数:
$$\begin{gathered} f_{xx}(x,y)=6x+6 \\ {f}_{xy}(x,y)=0 \\ {f}_{yy}(x,y)=-6y+6 \end{gathered}$$
对四个解分别计算A、B和C，考察定理2的条件。

• $(1,0):AC-B^2=12\times 6>0$且$A=12>0$，因此$(1,0)$是函数$f(x,y)$的一个极小值点，对应的极小值是$f(1,0)=-5$。
• $(1,2):AC-B^2=12\times (-6)<0$，因此$(1,2)$不是函数$f(x,y)$的极值点。
• $(-3,0):AC-B^2=(-12)\times 6<0$，因此$(-3,0)$不是函数$f(x,y)$的极值点。
• $(-3,2):AC-B^2=(-12)\times (-6)>0$且$A=-12<0$，因此$(-3,2)$是函数$f(x,y)$的一个极大值点，对应的极大值是$f(-3,2)=-31$。

拉格朗日乘子法

求函数$z=f(x,y)$在满足$g(x,y)=0$下的条件极值，可以转化为函数
$$F(x,y,\lambda )=f(x,y)+\lambda g(x,y)$$
的无约束条件极值问题。
例如，给定双曲线$xy=3$求该曲线上距离原点最近的点。这是一个典型的带约束的求极值问题。
原始问题可以转化为:
$$F(x,y,\lambda )=x^2+y^2+\lambda (xy-3)$$
计算函数$F(x,y,\lambda )$的一阶偏导，得到方程组:
$$\begin{gathered} F_x(x,y,\lambda )=2x+\lambda y=0 \\ {F}_y(x,y,\lambda )=2y+\lambda x=0 \\ {F}_{\lambda }(x,y,\lambda )=xy-3=0 \end{gathered}$$
求解该方程组，可以得到$\lambda =2$或$\lambda =-2$。当$\lambda =2$时，无法求解$x$和$y$，因为势必有$-x^2=3$。当$\lambda =-2$时，有两组解:$(3,3)$和$(-3,-3)$。